利用单位根给出一般周期数列的通项公式

☉浙江省温州中学 林庆望

☉浙江省温州大学 於家海

首先回顾周期数列的定义：给定数列{an}，如果存在不为0的正整数T，使得ai=ai+T对一切自然数i都成立，则称数列{an}称为周期数列，称T为这个数列的周期.例如a，b，c，a，b，c，…，一般要写出这个简单周期数列的通项并不困难，通常可以用分段通项公式来确定.但是如果想用一个统一的通项来表示，却不那么容易.下面我采用“分解组合”的思想，介绍利用单位根给出一般周期数列的通项公式.

一、退到最简单的情形

二、回到稍许复杂的情形

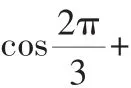
容易计算

有了上述准备，我们给出前述数列的通项公式为

三、推广到一般周期数列的情形

由前面的铺垫，我们想到类似的、更一般的周期数列的通项应该与单位根有关.不妨设所给数列的周期为k，即a1，a2，a3，…，ak，….先考查xk=1在复数域上根的分布情况，易见单位根分别为ω2=ω12，ω2=ω12，…，ωk=ω1k=1.我们当然希望xn可由这k个单位根来表示.由上面讨论我们可猜想周期为k的数列的通项公式为

下面给出该猜想的详细证明.对上述猜想，我们只需证明通项公式中ai的系数有且仅有一个为1，其余都为0，并且哪一个ai的系数为1，由n除以k的余数确定（r=n（modk））.特别地，当k整除n时，即ak的系数即为1；当k不整除n时，即ar的系数为0.下面分两种情况讨论：

即ak的系数为1.而∀r1=1，2，3，…，k－1而言，

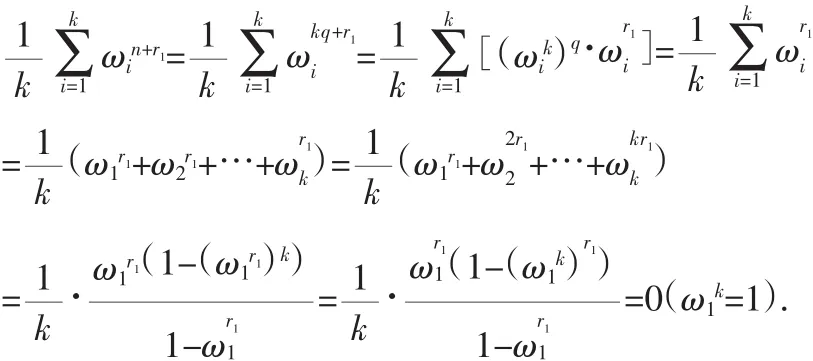
换句话说，这种情况下，除ak外，ar1的系数均为0.

而∀r1=1，2，…，r-1，r+1，…，k-1，k来说，

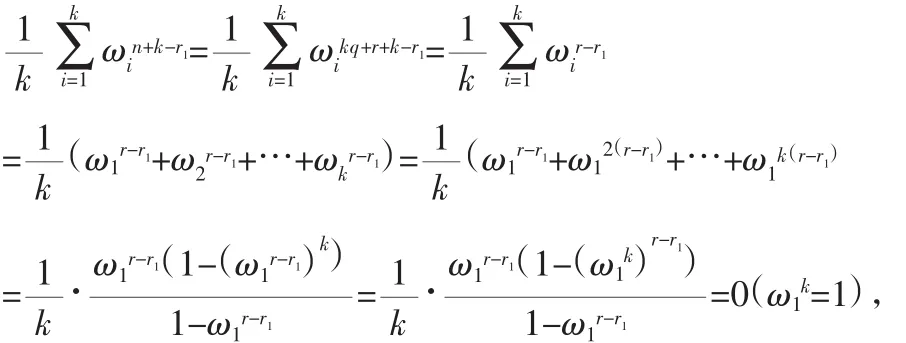
在这种情况下，除ar外，ar1的系数均为0.至此，我们证明了猜想的正确性.

四、一般周期数列再推广

我们还可以考虑这k个数中，可能会有相等的数字.如a，a，b，b，c，c，a，a，b，b，c，c，…，根据上面的论述我们容易得到它的通项公式为

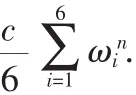
我们还可以考虑不均匀的情况，如a，a，a，a，b，b，b，c，c，d，a，a，a，a，b，b，b，c，c，…，不难发现该数列的通项公式为

其他情况，这里就不再赘述.

一点启示：数学大师华罗庚先生曾经说过：“我们要善于退，足够地退，退到原始而不失重要性的地方，退到我们容易看清问题的地方…”，从这个问题的解决过程来看，正是这样“退”的思想来指导我们获得解决问题的思路.今后我们遇到其他难题时，学会冷静分析，努力将问题分解成若干个简单问题，然后一一将它们攻克，再将这些简单问题进行适当组合，最终解决原来的问题.这种“分解组合”的思想，在数学问题解决中应该大有用武之地.