“旋转变换”迷人眼，“见微知著”深追问——2012年浙江义乌市中考第23题的思路突破与反思追问

☉浙江省绍兴市建功中学 曹 青

旋转变换是中考试题必考内容，很多中考卷都用旋转变换作为压轴题的命题形式呈现（如2012年浙江义乌卷第23题、北京卷第24题、四川南充卷第21题、四川成都卷第20题、2011年安徽卷第22题等）.突破这类问题需要看清旋转中心、旋转前后对应点、对应角、对应边，排除整个图形的干扰，善于分离出特殊位置下的图形（或极限情况）.下面我们结合2012年浙江义乌市中考第23题展开思路分析，并在解后反思中链接式展开一系列追问.当然，我们这种努力“指向”“入宝山不空返”（罗增儒语）.

例 （2012年浙江义乌市中考第23题）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1.

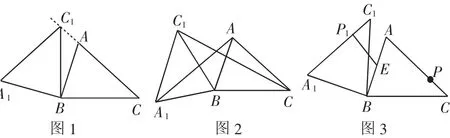
（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数.

（2）如图2，连AA1，CC1.若△ABA1的面积为4，求△CBC1的面积.

（3）如图3，点E为线段AB的中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值.

思路突破：

第一步，“特例引路”初感知

可以发现第（1）问中“点C1在线段CA的延长线上”是旋转后的特殊位置状态，标注出旋转前后的对应边、对应角，有∠A1C1B=∠ACB=45°、BC=BC1，进而得∠AC1B=∠ACB=45°，于是第（1）问获解.

第二步，发现“相似”快突破

在第（2）问中，考虑到旋转前后“∠ABC=∠A1BC1”⇒“∠ABA1=∠CBC1”，再看△ABA1和△CBC1是两个等腰三角形吗？能发现这两个三角形相似吗？问题不就突破了吗？要注意面积比等于相似比的平方哟！

第三步，“极限”位置获最值

初一看，很难理解.让我们先从边AC旋转后扫过的区域思考吧，容易发现当AC边旋转到直线AB上时，应该是点P到E的最值位置状态.此时最大值是点C（P运动到此点处）旋转到线段AB延长线上，此时最大值PE=7；最小值呢？刚才点P在C处时距离旋转中心B最远，想一想点P在AC何处时距离旋转中心B最短呢？过点B作BD⊥AC于D，此时的点B到直线AC最短距离为BD的长，相应的点P在此处，并旋转到AB边上时就获得最小值了！问题就获得了贯通.

试题简答：

（1）由旋转的性质可得∠A1C1B=∠ACB=45°，BC=BC1.

所以∠CC1B=∠C1CB=45°.

所以∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.

（2）因为△ABCS △A1BC1，所以BA=BA1，BC=BC1，∠ABC=∠A1BC1.

所以∠ABA1=∠CBC1.所以△ABA1S△CBC1.

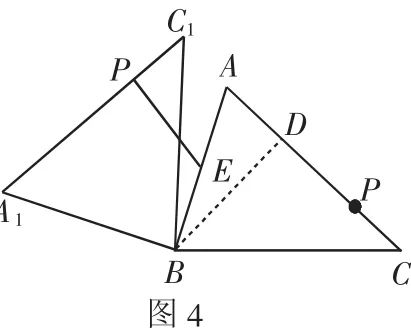
（3）过点B作BD⊥AC，D为垂足.

因为△ABC为锐角三角形，所以点D在线段AC上.

①当P在AC上运动至垂足点D，△ABC绕点B旋转，

使点P的对应点P1在线段AB上时，EP1最小，

②当P在AC上运动至点C，△ABC绕点B旋转，使点P的对应点P1在线段AB的延长线上时，EP1最大，最大值为2+5=7.

反思与追问：

决定性的是一步：

在第（3）问中，想到点P分别运动到C点处，并旋转到AB延长线上时，获得EP1最大值；进一步发现点P运动到D点处，并旋转到AB线段上时，获得EP1最小值.

主要困难在哪儿：

本题的最难点在旋转后点P到点E的最小值，一般情况容易误认为是P运动到A点时，当PE=AE=2时为最小值，这种错误在于疏忽了点B到直线AC的最小距离其实是垂线段BD的长.

“入宝山不空返”：

作为一道旋转变换的优秀试题，如果仅满足于上述求解是不够的，让我们链接着展开并继续追问，以便“入宝山不空返”.

链接：如图5，Rt△ABC绕O点逆时针旋转90°得到Rt△BDE，其中∠ACB=∠E=90°，AC=3，DE=5.则OC的长为（ ）.

讲解：根据旋转的性质，得BC=DE=5，BE=AC=3，则CE=8.根据旋转的性质可知△COE是等腰直角三角形，计算可得OC=OE=4

追问1：取OA中点M，P为AC上一动点，若将Rt△ABC绕O点旋转下去，则旋转后的P点到M点的距离最大值与最小值是多少呢？

讲解：有了最上面的分析，求出AB= 34，在等腰Rt△OAB，发现当P点在A处时，PM有最小值.最大值是点P在C点处时，旋转到AO的延长线上，此时

现在，我们还想做如下追问：

追问2：我们能否求出边AC绕点O旋转360°后扫过的面积？

讲解：这是一个圆环，大圆半径为4即圆环面积为15π.

追问3：怎样求边AB绕点O旋转360°后扫过的面积？

讲解：此时大圆的半径容易发现是，小圆的半径呢？应该是过O作AB的垂线段，长度是，此时圆环面积为

就让我们给义乌卷第23题增加一个第（4）问（第4次追问）留给读者自己思考吧！

追问4：边AC在旋转过程中扫过的图形是怎样的呢？我们能否求出边AC在旋转过程中扫过的面积？