利用图像解决与二次函数相关的问题

☉河南省开封市第十四中学 刘 震

初中已经学习了一元二次方程、二次函数的图像和性质，这些内容是高中学习函数的重要基础.高中数学并没有再安排二次函数的课题，二次函数的内容穿插到各章节之中，遇到的问题比初中复杂，难度变大，学生感到困难.这里向同学们介绍怎样通过数形结合的方法，利用二次函数的图像解决与二次函数相关的问题.

一、利用配方法和图像求二次函数的值域及其变式

例1已知f（x）=x2-4x-4，x∈［0，3］.

求函数的值域.

解：f（x）=（x-2）2-8，画出函数的图像.

如图1，观察图像知：

当x=0时，f（x）有最大值f（0）=-4；

当x=2时，f（x）有最小值f（2）=-8.

故函数的值域为［-8，-4］.

说明：解决上述问题的步骤是：①配方；②本着先虚（定义域外）后实（定义域内）的原则画出图像；③根据上大下小的原则确定函数的值域.

例2 已知二次方程x2-4x-4-a=0在［0，3］上有解，求实数a的取值范围.

错解：由Δ=（-4）2-4×1×（-4-a）≥0，得a≥-8.

这是因为上述解法只保证方程有解，不保证解在［0，3］内.

正解：原方程在［0，3］上有解⇔x∈［0，3］时，函数a=x2-4x-4的值存在.

由例1知a∈［-8，-4］.

例3 已知对任意x∈［0，3］，x2-4x-4-a＜0恒成立，求实数a的取值范围.

解：由原不等式得a＜x2-4x-4.

设t=x2-4x-4，x∈［0，3］，

由例1知t∈［-8，-4］.

又对任意x∈［0，3］，a＞t恒成立，

故a＞-4.

例4已知f（x）=x2-4x-4，x∈［t，t+1］.若f（x）的最小值为g（t），求g（t）的解析式.

解：f（x）=（x-2）2-8.

（1）当t＜1时，t+1＜2，观察图像知：

g（t）=f（t+1）=（t+1）2-4（t+1）-4=t2-2t-7.

（2）当1≤t≤2，t+1≥2，观察图像知g（t）=-8.

（3）当t＞2时，观察图像知：

g（t）=f（t）=t2-4t-4.

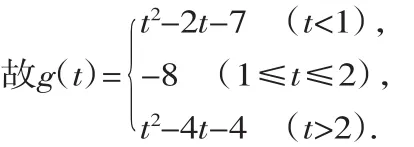
二、利用图像解决与二次函数性质相关的问题

例5函数f（x）=x2-2ax-3在区间［1，2］上存在反函数的充要条件是（ ）.

A.a∈（-∞，1］ B.a∈［2，+∞）

C.a∈［1，2］ D.a∈（-∞，1］∪［2，+∞）

解：f（x）=（x-a）2-a2-3.

（1）当抛物线的对称轴直线x=a在区间［1，2］的左侧，即x≤1时，函数单调递增；

（2）当抛物线的对称轴直线x=a在区间［1，2］的右侧，即x≥2时，函数单调递减.

故f（x）在［1，2］上存在反函数的充要条件是a∈（-∞，1］∪［2，+∞），选D.

例6如果函数f（x）=x2+bx+c对任意实数t都有f（2+t）=f（2-t），那么f（1），f（2），f（4）从大到小的排序为______.

解：由f（2+t）=f（2-t），

知抛物线的对称轴为直线x=2.

画出函数的图像如图2，观察图像知：

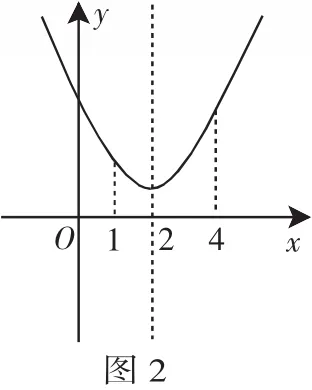
说明：设f（x）是二次函数，

三、利用图像解决一元二次方程根的分布问题

例7已知二次函数f（x）=2（k+1）x2-（k2-3）x-（k-1）的图像与x轴有两个交点，这两个交点分别在点（-1，0）的两侧，求k的取值范围.

解：（1）当2（k+1）＞0时，y=f（x）的图像如图3所示，需满足f（-1）＜0.

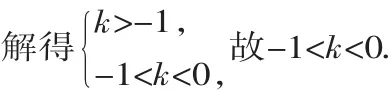
（2）当2（k+1）＜0时，y=f（x）的图像如图4所示，需满足f（-1）＞0.

综合（1）（2）知，k＜-1或-1＜k＜0.

例8 方程x2-6x+4a2-3=0有绝对值不大于1的实数解，求其中a的取值范围.

解：设f（x）=x2-6x+4a2-3，使f（x）=0.

有根x∈［-1，1］，注意对称轴方程为直线x=3.

画出函数y=f（x）的图像如图5所示，则它与x轴在对称轴左侧的交点位于［-1，1］内.

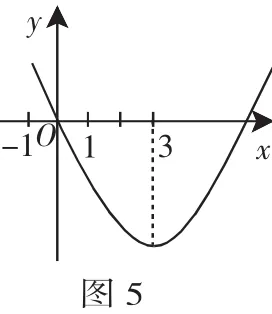
说明：一元二次方程的根的分布问题在形上的体现就是抛物线与x轴交点的位置问题.

四、综合应用

例9 已知函数y=x2-2ax+a2-1在［0，1］上为减函数，问当a取何值时，在［0，1］上y＞0恒成立.

解：由y=x2-2ax+a2-1配方得y=（xa）2-1，对称轴方程为x=a，顶点坐标为（a，-1）

（1）要使x∈［0，1］时f（x）是减函数，需函数y=f（x）的图像如图6所示，则对称轴在直线x=1或直线x=1的右侧，需满足a≥1；

（2）要使x∈［0，1］上f（x）＞0恒成立，注意在a≥1的条件下，函数y=f（x）的图像如图7所示，需使f（1）＞0，即1-2a+a2-1＞0，解得a＜0或a＞2.故a＞2为所求.

练一练：

1.设函数f（x）=ax2+bx+c，已知f（x）=0的两根分别在区间（1，2）和（2，3）.则（ ）.

A.f（1）f（2）＞0B.f（1）f（2）＜0

C.f（1）f（3）＜0D.f（2）f（3）＞0

答：B

2.已知f（x）=4x2-4ax+a2-2a+2在区间［0，2］上有最小值3，求实数a的取值的集合.

（1） 当a＜0时，f （x）min=f （0）=a2-2a+2使a2-2a+2=3， 得a=1-

（3）当a＞4时，f（x）min=f（2）=a2-10a+18，使a2-10a+18=3，得a=