用数值代入的方法证明平面几何题
2012-08-27 02:42上海市新黄浦实验学校
中学数学杂志 2012年4期
☉上海市新黄浦实验学校 许 敏
平面几何中的证明题很多可以用数值代入的方法去证明,其基本思想是这样的:首先将几何证明中的点的坐标用符号来表示,然后将几何条件转化为代数求解问题,最后对给定的符号用具体的数值来代替,从而达到证明的目的.
1.将几何证明问题转化为代数问题
例1 证明正方形的对角线互相垂直平分.
分析:首先设定正方形的四个顶点的坐标,假设已知正方形ABCD以AD为x轴,以AB为y轴,边长为a,则A、B、C、D坐标分别为A(0,0),B(0,a),C(a,a),D(a,0).则直线AC的解析式为y=x,直线BD的解析式为y=a-x.证明对角线互相垂直平分,则需要证明|AE|=|EC|,|BE|=|ED|,而且AC⊥BD.因此,该几何证明题可转化为代数问题为:
1.证明直线AC与直线BD垂直:直线AC和BD的斜率都可表示为关于a的表达式,接着证明两斜率的乘积为-1.
2.|AE|=|EC|,|BE|=|ED|:线段AE、EC、BE、ED的长度都可以转化为关于a的表达式,然后来证明其对应的关于a的代数表达式的等号左右两边相等.


以上用这个例子来说明如何将几何问题转化为代数问题,并且阐述如何用代数的方法来解几何问题.对于简单的几何问题,它所涉及的符号比较少,如例1,我们只需要设一个符号就可以把其余的点的坐标表示出来.但是,对于很多几何问题,它所涉及的符号太多,在推理以及计算过程中非常复杂,如果用例1的方法来处理将十分困难,接下来我们讨论如何用具体数值代入的方法来证明几何题.
2.具体数值代入法

具体数值代入法是将代数问题中出现的符号直接用随机取的数值代入进行计算和证明.我们用下面的例子来描述该方法.
例2 证明三角形三条中线交于一点.


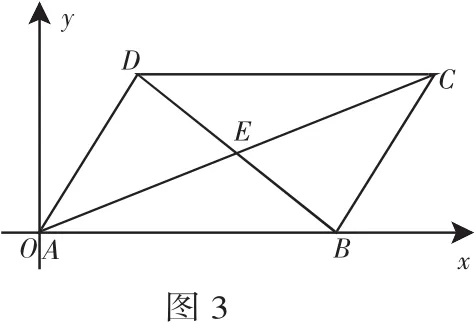
例3 平行四边形对角线互相平分.
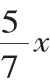
猜你喜欢
数学小灵通(1-2年级)(2021年5期)2021-07-21
小学生学习指导(中年级)(2021年4期)2021-04-27
河北理科教学研究(2021年4期)2021-04-19
科学(2020年1期)2020-08-24
数学小灵通(1-2年级)(2020年4期)2020-06-24
小学生学习指导(低年级)(2018年12期)2018-12-29
小学生导刊(2018年34期)2018-12-18
中学生数理化·八年级数学人教版(2016年2期)2016-04-13
中学生数理化·八年级数学人教版(2016年3期)2016-04-13
中学数学杂志(高中版)(2016年1期)2016-02-23

