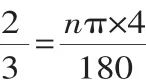盘点近几年中考中与线段相关的一类最值问题

☉浙江省上虞市竺可桢中学 徐 骏

近年来，与线段相关的一类最值问题在各地市中考试卷中大量涌现，并成为近几年中考的热点题型之一.这类问题对知识和技能要求较高，能够考查学生分析问题和解决问题的能力与创新意识.解决此类问题主要借助以下3个知识点：（1）两点之间线段最短；（2）三角形的任意两边之和大于第三边，任意两边之差小于第三边；（3）直线外一点与直线上各点连接的所有线段中，垂线段最短.笔者结合近几年中考数学试题，对于常见的线段最值问题，归纳为以下几大块，以帮助学生掌握这类问题的求解方法.

1.一条线段的最值问题

1.1 求一条线段的最大值

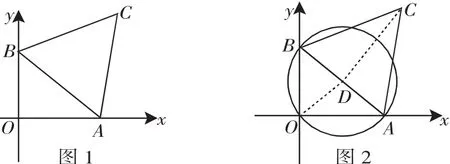
例1 如图1，边长为a的正三角形ABC，两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则OC的长的最大值是_______.

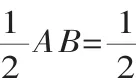
1.2 求一条线段的最小值

例2 如图3，在平面直角坐标系中，以坐标原点O为圆心，2为半径画⊙O，P是⊙O上一动点，且P在第一象限内，过点P作⊙O的切线与x轴相交于点A，与y轴相交于点B.点P在运动时，线段AB的长度也在发生变化，请写出线段AB长度的最小值，并说明理由.

分析 连接OP（如图4），因为AB切⊙O于P，所以OP⊥AB.取AB的中点C，则AB=2OC.当OC=OP时，OC最短，即AB最短，此时AB=4，所以线段AB长度的最小值为4.

例3 如图5，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CB，CA分别相交于点E，F，则线段EF长度的最小值是（ ）.

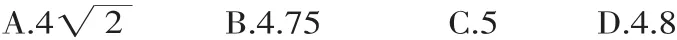
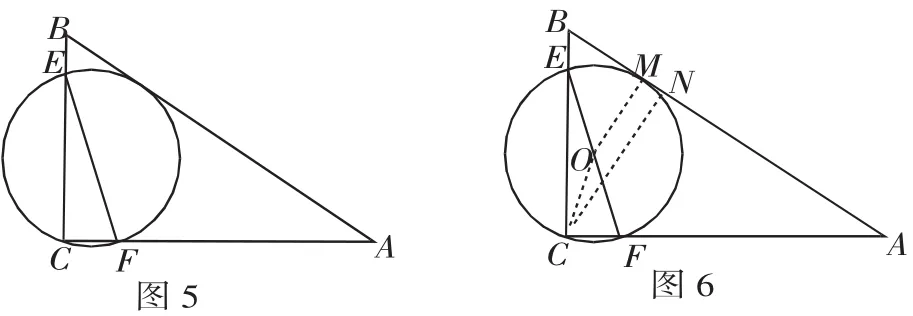
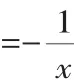
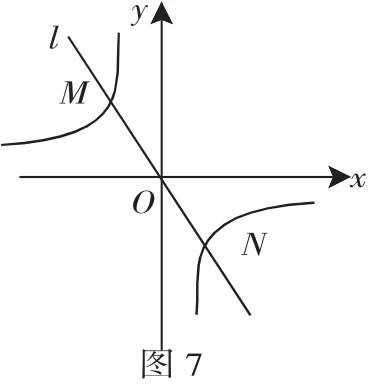
分析 设M（a，b），则ab=-1.由（a+b）2=a2+2ab+b2≥0，得a2+b2≥-2ab=2.由中心对称性知，MN=2OM=2，所以线段MN的长的最小值

2.两条线段的最值问题

2.1 求两条线段和的最小值

例5 如图8，在锐角△ABC中，AB=4，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD和AB上的动点，则BM+MN的最小值是_______.

分析 如图9，作点N关于直线AD的对称点N′，连接BN′，则BM+MN=BN′的值最小.过点B作BE⊥AC于E，在Rt△ABE中，BE=AB·sin45°=4.当BN′=BE时，BN′最短，即BM+MN的值最小，所以BM+MN的最小值是4.

2.2 求两条线段差的最大值

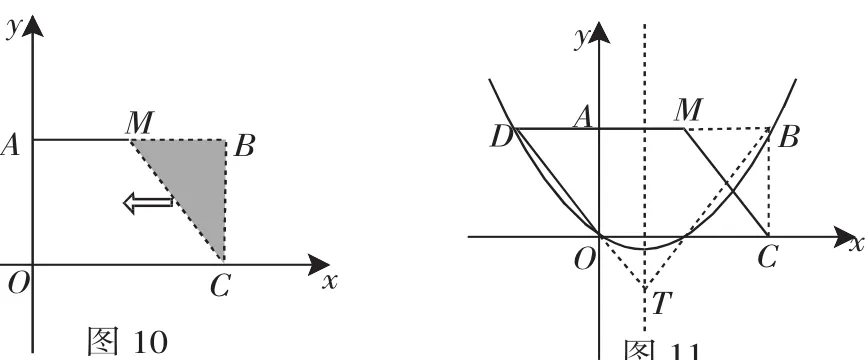
例6已知：如图10，把矩形OCBA放置于直角坐标系中，OC=3，BC=2，取AB的中点M，连接MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO.已知点B与点D在经过原点的抛物线上，试问在抛物线的对称轴上是否存在一点T，使得TO-TB的值最大.

3.三条线段的最值问题

例7 如图12，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.当M点在何处时，AM+BM+CM的值最小，并说明理由.

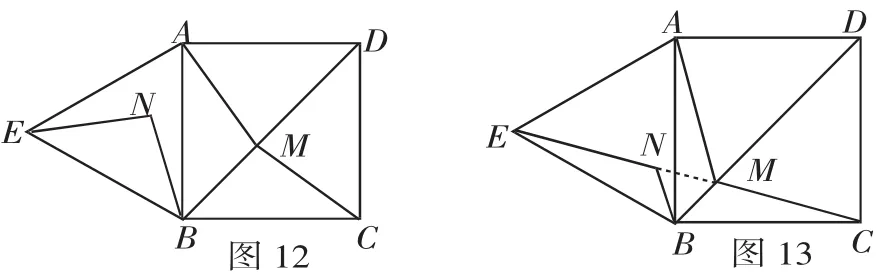
分析 如图13，连接CE，当M点位于BD与CE的交点处时，AM+BM+CM的值最小.理由如下：连接MN，由∠MBN=60°，BM=BN知，△BMN是等边三角形，则BM=MN.易证△ABM≌△EBN，则AM=EN.根据“两点之间线段最短”，得AM+BM+CM=EN+MN+CM=EC最短，所以当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长.

4.三角形周长的最值问题

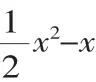
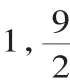
5.四边形周长的最值问题

例9 如图16，将两张长为8，宽为2的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的周长有最小值8，那么菱形周长的最大值是_______.

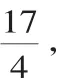
例10 如图18，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系.已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处.在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由.

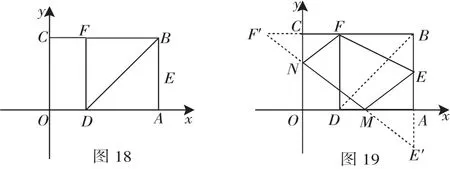
分析 存在点M、N，使得四边形MNFE的周长最小.理由如下：如图19，作点E关于x轴的对称点E′，作点F关于y轴的对称点F′，连接E′F′，分别与x轴、y轴交于一点，则这两点分别为所求点M、N，使四边形MNFE的周长最小.而E′（3，-1）、F′（-1，2），NF=NF′，ME=ME′，所以BF′=4，BE′=3，所以FN+NM+ME=FN+NM+ME′=F′E′=

6.几何体侧面上的一类最值问题

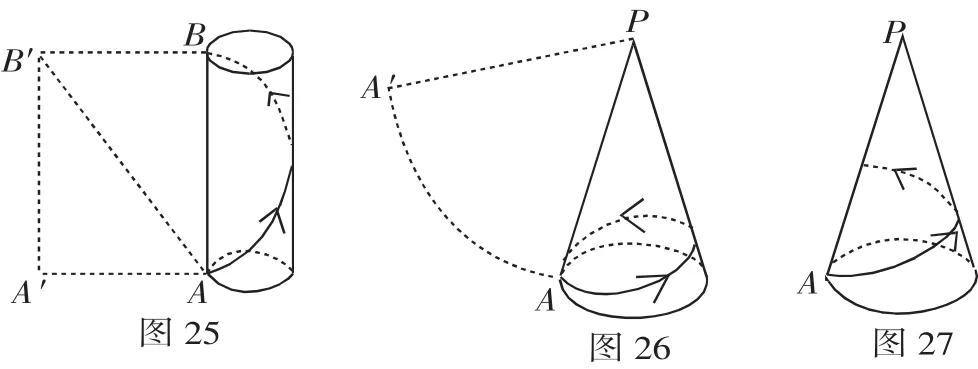
例11 如图20，长方体的底面边长分别为1cm和3cm，高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要____cm；如果从点A开始经过4个侧面缠绕n圈到达点B，那么所用细线最短需要________cm.

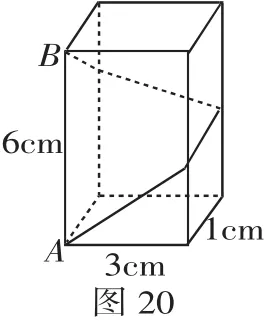
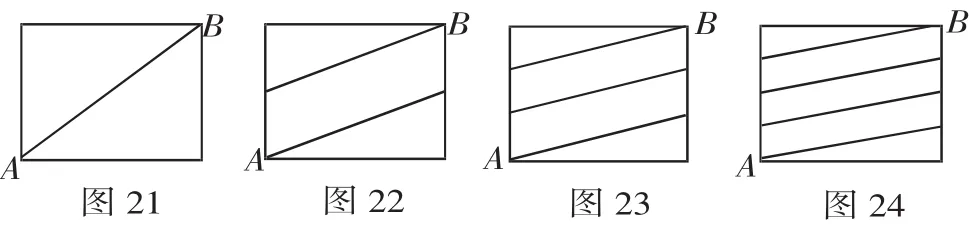
分析 长方体的侧面展开图是一个长为8cm，宽为6cm的矩形.如图21，如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要需要4cm；依次类推，如果从点A开始经过4个侧面缠绕n圈到达点B，那么所用细线最短需要n

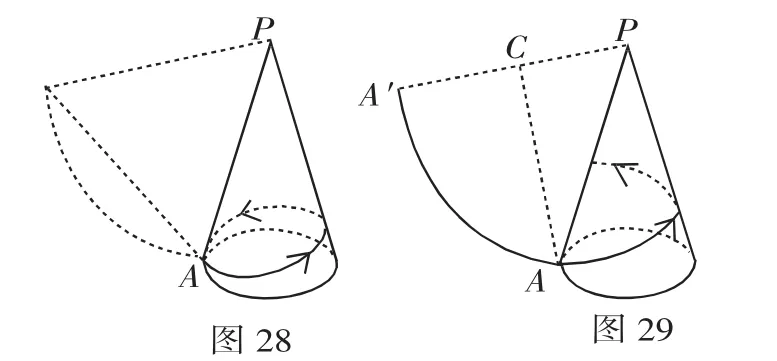
例12 问题探究：

（3）如图27所示，在（2）的条件下，一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点，求蚂蚁爬行的最短路程.