例谈一元二次函数的取值问题

☉浙江省杭州师范大学附属中学 谢黎静

一元二次函数是初中教材中的重点内容，但难度要求不高，到高中进行了深化，在学习中我们发现不光它的内容应用广泛而且它渗透了一些很重要的数学思想方法（如数形结合、分类讨论等），而其中最能体现一元二次函数上述特点的是：解决一元二次函数在区间上的取值问题.此知识的考查在高考中很常见.一元二次函数在区间上的取值问题可以通过对称轴和区间是否含有参数细分成四种类型，下面笔者通过一些例题来加以说明.

一、对称轴和区间都不含参数的类型

例1求函数（fx）=x2－2x+2在区间［0，1］上的最小值.

分析：此函数的对称轴为x=1，结合图像可知函数在区间［0，1］上单调递减，则函数的最小值为f（1）=1.

二、对称轴不含参数、区间含参数的类型

例2函数f（x）=x2－2x+2在区间［t，t+1］上的最小值为2，求t的值.

分析：区间位置会随着t变化，而函数的对称轴位置和函数图像开口方向都确定，结合函数图像此题应按对称轴在区间的左侧、中间、右侧三种情况进行讨论.

解：函数的对称轴为x=1.

当对称轴在区间左侧，即t＞1时，函数在区间［t，t+1］上单调递增，即fmin（x）=f（t）=t2－2t+2=2，则t=0（舍去）或t=2.

当对称轴在区间内，即0≤t≤1时，函数的最小值在顶点处取得，即fmin（x）=f（1）.又f（1）≠2，则0≤t≤1舍去.

当对称轴在区间右侧，即t＜0时，函数在区间［t，t+1］上单调递减，即fmin（x）=f（t+1）=t2+1=2，t=1（舍去）或t=－1.

综上：t=2或t=-1.

例3函数f（x）=x2－2x+2在区间［t,t+1］上的最大值记为h（t），求h（t）的最小值.

分析：区间位置会随着t变化，而函数的对称轴位置和函数图像开口方向都确定，结合函数图像此题应按对称轴在区间的左侧、中间、右侧三种情况进行讨论.当然又由函数对称性可知，函数图像开口向上，对称轴在区间中间时，区间端点离对称轴的距离大小影响最大值取到的可能性.

解：函数的对称轴为x=1.

当对称轴在区间左侧，即t＞1时，函数在区间［t，t+1］上单调递增，即h（t）=f（t+1）=t2+1.

当对称轴在区间右侧，即t＜0时，函数在区间［t，t+1］上单调递减，即h（t）=f（t）=t2－2t+2.

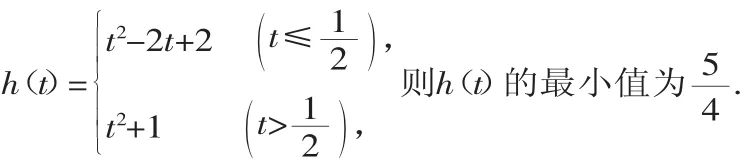
当然对于开口向下的一元二次函数求最小值的分类讨论也与上例类似.

三、对称轴含参数、区间不含参数的类型

例4函数f（x）=x2－2tx+2在区间［0,1］上的最大值为2，求t.

分析：此函数对称轴为x=t，位置不确定，区间位置和函数图像开口方向确定，结合函数图像此题应按对称轴在区间的左侧、中间、右侧三种情况进行讨论，当然又由函数对称性可知，函数图像开口向上，对称轴在区间中间时，区间端点离对称轴的距离大小影响最大值取到的可能性.

解：此二次函数的对称轴为x=t.

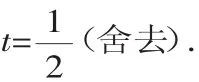
当对称轴在区间右侧，即t＞1时，函数在区间［0,1］上单调递减，即2=fmax（x）=f（0），而f（0）=2恒成立，则t＞1.

四、对称轴和区间都含参数的类型

例5已知函数f（x）=t＞0），求函数f（x）的最小值.

分析：此函数中含有绝对值，要求最值，先需对绝对值进行讨论，再求相应的最值.

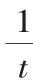
总之，事实上，通过对称轴和区间是否含有参数的分类，任何一个一元二次函数在闭区间上的最值问题都可以归类到以上某种类型，而以上每种类型中最值问题的求解都离不开对函数图像开口方向和对称轴与区间相对位置的把握，并运用数形结合和分类讨论的思想方法.