数形结合思想热点应用举例

☉河南省汝州市第一高级中学 王二品

所谓数形结合思想，简而言之就是代数问题几何化、几何问题代数化，充分利用图形的直观性和代数推理的合理性、严密性研究问题.数与形是数学研究的两个重要方面，在研究过程中，数形结合既是一种重要的数学思想，又是一种常用的数学方法.数形结合是历届高考的重点和热点.数形结合包含“以形助数”和“以数辅形”两个方面，其中“以形助数”是其主要方面，其方法的关键是根据题设条件和探求目标，联想或构造出一个恰当的图形，利用图形探求解题途径.对于填空题可以简捷地直接获得问题的结果，对于解答题要重视数形转换的等价性论述，避免利用图形的直观性代替逻辑推理得到结果.“数缺形时少直观，形少数时难入微”，利用数形结合的思想方法可以深刻揭示数学问题的本质.函数的图像、方程表示的曲线、集合中的韦恩图或数轴表示等，是“以形示数”，而解析几何中的方程、斜率、距离公式、向量的坐标表示等则是“以数助形”，还有导数更是数形结合的产物，这些都为我们提供了“数形结合”的知识平台.下面举例说明数形结合思想的热点应用.

一、在集合中的应用

二、数形结合在函数中的应用

函数的图像是函数关系的一种表示，它是从“形”的方面刻画函数的变化规律.函数图像形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探究解题途径、获得问题结果的重要工具.函数图像和解析式是函数关系的主要表现形式，实质是相同的，在解题时经常要互相转化，尤其是在处理较为烦琐的问题时，要充分发挥图像的直观作用.

三、数形结合在向量中的应用

向量作为数学的一个基本概念，成了沟通代数、几何与三角函数的工具.由于既有代数表示，也有几何表示，成为了数形结合的重要载体.

四、数形结合在解析几何中的应用

解析几何主要研究的是图形的特征以及图像间的位置关系.初中是直接运用定理进行证明研究，高中则是通过建立直角坐标系，用点的坐标和曲线的方程，通过代数方法来计算图形的特征和位置关系等问题，其本质原因是高中阶段对几何问题的研究牵涉具体的长度、角度、面积等，故需要用代数方法来研究几何问题.

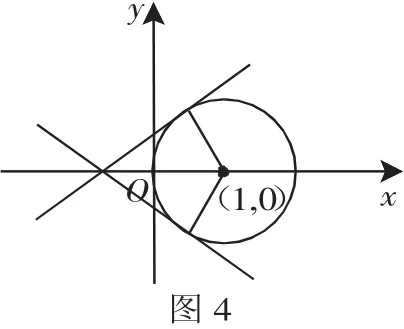
例4 （2011年江西）若曲线C1：x2+y2-2x=0与曲线C2：y（ymx-m）=0有四个不同的交点，则实数m的取值范围是（ ）.