一类向量考题的快速解法初探

☉江苏省镇江市丹徒高级中学 吴海军 邱红英

从近几年的各省高考中向量的考题来看，对向量的考查主要集中在判断三角形的形状，判断点所处的位置，判断动点的轨迹，利用其几何意义解题等方面，尽管常以小题形式出现，但往往让考生们无从下手，可见其重要地位.

这里我们来探讨一下2008年浙江卷的第9题.

例1（浙江卷9）已知a、b是平面内两个互相垂直的单位向量，若向量c满足（a-c）·（b-c）=0最大值是（ ）.

分析1：向量问题是数形结合思想体现最突出的问题，所以我们尝试利用几何意义解题.

解法1：由（a-c）·（b-c）=0，得（a-c）⊥（b-c）.

又a、b互相垂直，则a、b、a-c、b-c构成的四边形是圆内接四边形，且c恰好是四边形的对角线.当c是直径

取得最大值，此时圆内接四边形是以a、b为邻边的正方形，所以有

分析2：这道题用几何意义来解虽然计算量小，但是很多学生的思维水平和分析能力远远达不到这样的高度，很难将“两组向量垂直”与“圆内接四边形”联系起来.在这种情况下，我们不妨试试坐标法.

解法2：a、b是平面内两个互相垂直的单位向量.

建立平面直角坐标系，设a=（1，0），b=（0，1），c=（x，y）.

a-c=（1-x，-y），b-c=（-x，1-y）.

由（a-c）·（b-c）=0，得（1-x）（-x）+（-y）（1-y）=0.

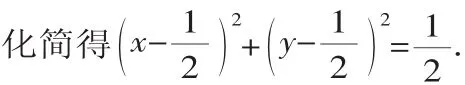
所以向量c的起点（即坐标原点）在圆上，终点也在圆上，因为原点O到圆上的点的最大值等于圆的直径，所以有

解法2运用坐标法，只需建系，设坐标，直接利用坐标运算找出向量c的终点坐标的轨迹方程.整个解题过程周密严谨，说服力强，可靠性高，是做题能力不强的学生的首选方法.

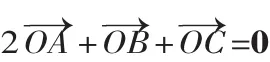
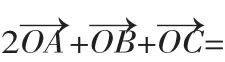
反思：通过以上三种方法，我们发现遇到此类问题只要用坐标法就可以化复杂为简单，省却了用图像法分析向量间的关系的诸多麻烦.

分析：本题与例2相似，只是问法有所不同，下面我们给出一种解法，另两种解法大家可以自行验证.

例4 （2011年高考新课标全国卷文13）已知a与b为两个不共线的单位向量，k为实数，若向量a+b与向量ka-b垂直，则k=________.

分析：这道高考题如果用坐标法解，就非常简单.

解：根据题意，不妨设a=（1，0），b=（0，1），则a+b=（1，1），ka-b=（k，-1）.因为a+b与向量ka-b垂直，所以（a+b）·（ka-b）=0，即k-1=0，解得k=1.

解题反思：考场上的时间是宝贵的，能够在高考紧张的状态下寻求快捷有效的解题方法是高考制胜的关键.面对向量题，要想在短时间内通过作图利用几何意义，需要较高的思维能力.而采用坐标法，其优势是明显的，尤其是解例2、例3这类题型，对相对点所提的位置要求只有一个，在这样的情况下，设△ABC的任两个顶点为特殊点，求出第三个点，都能够用逻辑严谨的过程解决相应问题.当然，创新无止境，研究不可浅尝辄止，围绕这一方法，我们在尝试的过程中肯定还会遇到新的问题，让我们一起探究下去吧！