反例在教学中的探索
谢月花
(苏州市相城区陆幕实验小学 江苏 苏州 215131)
1 反例的教学功能
1.1 有利于加深概念理解
反例能够有效帮助学生加深概念的理解,包括定理、法则、公式,而定理、法则、公式的掌握有利于帮助学生解决一些简单的问题。但是,现实教学中,我发现学生在使用它们时,经常会漏掉某条件,忽略某关键字。为了防患于未然,教师需要加强定理、法则、公式的产生过程的教学,增加学生自主探索定理、法则、公式的机会,针对定理、法则、公式中的一些条件、关键字进行必要反例教学,从而帮助学生牢固掌握概念,达到“去伪存真”的效果。
例:在三角形全等判定方法的教学中,对于判定方法 “如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等”,个别学生会提出这样的问题:“条件中的夹角能否换成一边的对角?”针对学生的疑问,同时也为了告诫学生条件中的“夹”不能忽视,教师经常构造以下反例:先作一个等腰△ACD,再延长底边DC到B,连接AB(如图1),则在△ABC与△DBC中,AB=AB,AC=AD,∠ABC=∠ABD,但△ABC 与△DBC 并不全等。
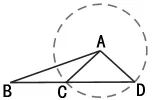
图1 -1
1.2 有利于澄清错误认识
在学习之中常常由于思维定式的影响,会想当然得出一些经不起推敲的结论。时适时的举出反例,就会使得对题目印象深刻,深入领悟本质。
例:在学习“反函数图像对称”时,许多同学会认为:互为反函数的两个函数图像相交的交点一定在直线y=x上,我们可以举出一个反例的交点之一(1,2)就不在y=x上。
1.3 反例是否定命题的重要方法
要否定一个命题,可用归谬法或证明法,但是简明而又有说服力的,则是举出其反例。
例:命题“无理数的无理数次幂仍为无理数”是否成立?
这就说明,命题不成立。
1.4 反例对肯定命题的作用
如果否定了一个命题的所有反例,是否就证明了这个命题是成立的?答案是肯定的!
例:求证:两条直线相交只有一个交点。
分析:正面论证是很困难的,反过来考虑所有反例:“两条直线相交不止一个交点”的情况,若能经过推理否定了该反例,则原命题得证。
证明:假设两条直线相交不止一个交点,不妨设有A,B两个交点。因为两点确定一条直线,所以经过点A,B的直线只有一条,与已知两条直线矛盾。即两条直线相交只有一个交点。
2 反例对学生思维能力的培养
2.1 注重反例教学培养学生的逆向思维能力
逆向思维是从已有的习惯思路的反方向去思考和分析问题。在数学学习中的某些概念、定理、性质和法则都比较抽象,学生难以理解。在教学时,教师必须让学生从正面去理解有关知识,并举例加以巩固,而恰当地运用反例可以使学生加深对所学知识的理解和掌握,也有利于培养学生的逆向思维能力。
2.2 注重反例教学培养学生的侧向思维能力
侧向思维是从知识之间的横向相似联系出发去模拟、仿造或分析问题的思维方式。在数学学习中的证明两个三角形相似,三角形全等等知识之间存在着某些联系。在教学中,我们可以利用相互间的联系,用自己熟悉的方法去认识新的定理、性质等知识,用类似的反例去否定新的谬误,使学生尽快地理解和掌握新知识,当然也有利于培养学生的侧向思维能力。
2.3 注重反例教学培养学生的多向思维能力
多向思维是从尽可能多的方面来考察同一问题,使思维不局限于一种模式或一个方向,从而获得多种解答或多种结果的思维方式。多向思维在解决问题时有三种基本形式:一题多解、一法多用、一题多变。在数学教学中,对于一个假命题可以用多个反例,对于同一个例子可以作为多个命题的反例,我们还可以多次改变真命题的部分条件,构造多个假命题,然后逐一用反例将其否定,以加深对原命题的理解。这样不但可以使学生明白命题错误的根源,纠正错误,加深其对所学知识的理解,而且更有利于学生多向思维能力的培养。
我国原本的应试教育已逐步淘汰,取而代之的是素质教育的新时代。数学教学也充满了灵活多样、开放、动态的特点,创新思维能力和综合能力的培养成为教学的重点。因此,在数学教学中,根据学生存在的问题,进行反例教学,逐步培养学生的思维能力,提高学生自学能力及分析、解决问题的能力。
3 实施反例教学要注意的问题
反例教学既有其极其重要的作用,也有其在实施的过程中需要注意的环节。
3.1 注意反例教学的引人
由于学生年龄、生理和心理特征以及认知结构的不完整性,他们的思维受到一定的局限性,考虑问题可能还会不够周全,在教学过程中教师应该注意到反例教学引入的合理性和可行性。
3.2 注意反例教学的构建
在进行教学时,教师不仅要恰地使用反例,更重要的是要引导学生构建反例,这实际上是为学生获取知识创设了一种探索的情景。一般情况下,许多反例的构建不是唯一的,这时候教师可选择一些典型的数学知识或问题,通过创设问题情景,引导学生构建反例,使学生敢于和善于发现问题、提出问题、分析问题,解决问题,从而提高学生的思维能力。
因此,学生构建反例的过程也是他们思维发挥和训练过程。
3.3 注意反例教学的逐层深入性
在教学时,反例教学的使用必须建立在学生对概念有一定理解的基础上,若在学生刚刚接触概念时就使用,会导致学生先入为主,从而干扰其对概念的掌握。反例的构建要根据学生的认知发展水平和已有的认知结构逐步进行,把某些难度较大的问题转化为一些简单易懂的题目。
总之,数学反例是数学课堂教学中一个有效的调节器,在数学教学中,适时地引进一些反例或者适当地引导学生构建反例,往往能使学生在认识上产生质的飞跃,从而帮助他们巩固和掌握知识,培养他们思维的严谨性、灵活性、发散性、逻辑性、创新性和全面性。
4 反例的教学局限性
教师在教学过程中要有意识地积累各块知识中经典的反例,对于关键知识点教学是十分有益的。同时可以适时鼓励学生自己举出需要的反例,以增进认知。然而,正例与反例在教学中要适度应用,反例教学如果把握不好,容易产生副作用,需要警惕。不恰当地应用反例,主要有以下表现:
4.1 过早进行反例教学,会使得主次颠倒、喧宾夺主
在我们的教学中应把把握重点,对教学重点精讲细练,等到学生对正面题意有深刻领会、理解之后,再适当地出示反例,让学生更深层次的理解题目。
4.2 过于强调反例,会给学生造成心理压力
学生的认知能力及思维发展存在着一定的差异,部分同学接受知识的能力存在一定的滞后性,掌握理解知识需要一个慢慢消化吸收的过程。如果这时候教师过于强调反例,会给学生发出错误信号:你随时都会出错!这将会让学生认为自己做题时出错是在所难免的,从而打击学生的自信心,失去对数学的兴趣。
4.3 过多使用反例,不符合学生的记忆规律
心理学表明:强烈的记忆意图使人注意力集中,记忆效果良好;反之,则会降低注意力,造成遗忘。“过多”的使用反例教学会逐步淡化“正例 ”的记忆效果,使学生思考问题专门从反面入手,而有些题目不适合从反面思考,这样使得教学效果适得其反。正如教师最讨厌的“该记的没记住,不该记的全记住了”。
综上所述,数学教学中离不开反例,也不能处处都用反例。我们要以正例为主,反例为辅,才能使例题教学达到预期的效果。
[1]罗腾根.浅谈反例的教学功能与构造方法[J].中学数学教学参考,1996(11):5-6.
[2]彭光焰.例谈反例的教学功能[J].数学通报,2002(8):16-18.
[3]何华兴.数学反例的教学价值[J].数学教学通讯,2004(6):30-32.
[4]林美娟.注重反例教学,培养学生的发散思维能力[J].科技信息,2008(31):644-645.

