基于流固耦合算法的罐车防波板的分析

周 斌 马 力 张中正

（武汉理工大学 湖北 武汉 430070）

0 引言

罐车的防波板可以在其运行时减弱罐体内液体的冲击和吸收液体的振动能量，从而提高罐车的行驶稳定性和安全性。故对防波板进行强度校核和改进设计是十分必要的。相对于只考虑流体运动的计算方法，流固耦合算法所得结果更加准确。利用流固耦合效应分析工程问题主要应用于航空和船舶工业，在汽车工业上的应用还不广泛，对罐车进行流固耦合计算的研究还很少。北京理工大学宇航学院的周思达和刘莉在2010年6月阐述了运载火箭贮箱流固耦合的常用分析方法。2010年8月，向韬[2]等在考虑流固耦合效应的基础上运用Adina对某油罐车进行有限元分析，得到了罐车在几种典型工况下的应力分布及液面的分布情况。用流固耦合算法对防波板进行分析目前尚处于空白。本文通过Ansys软件模拟罐车制动时罐体内介质的晃动对两阻尼孔防波板产生的应力与应变，并对其强度行了校核。同时对比了防波板上阻尼孔的孔径、孔位与孔数的不同对罐内介质流动及罐体所受应力的影响，为防波板的进一步改进设计提供了真实有效的数据。

1 两阻尼孔防波板模型的建立

令罐车行驶的方向为x正方向，由于罐体关于中轴对称，为了减少计算量，只需在Ansys中建立介质和防波板的1/2几何模型，依次沿x负方向定义为：b1、b2、b3，其中b1和b2间的距离为2850mm，b2和b3间的距离为2900mm，材料为Q345，完成后如图1所示。

图1 防波板的几何模型

因为罐内介质是气态和液态共存，故在ANSYS软件中采用多相流来模拟介质。设主相为液态，第二相为气态，设定二相所包含的网格是以充装系数为依据，取0.83为最大充装系数。定义507kg/为液体介质的密度，2.0为动力粘度，1.81kg/为气体介质的密度，8.1为动力粘度。流体的湍流模型选择标准模型，制动时的减速度为-9.81m/。

2 计算结果分析

在流固耦合计算过程中，通过监测防波板b1、b2和b3在x方向合力的变化情况，得到如图2所示的b1、b2、b3在2s内x方向受力变化的曲线。由图2可以看出，在前0.7s内b1、b2和b3变化趋势基本一致，b1会在0.32s是出现x负方向最大合力9061N，b2和b3都在在0.26s是出现x负方向最大合力8936N和8315N。在0.7s后变化趋势不同，说明在前0.7s内介质的晃动步调几乎是一致的，0.7s后介质晃动步调差异十分的显著。b1、b2和b3在x方向的合力会出现正值，这是因为在介质在晃动过程中，出现了向x正向的涌动，这与实际情况相符。

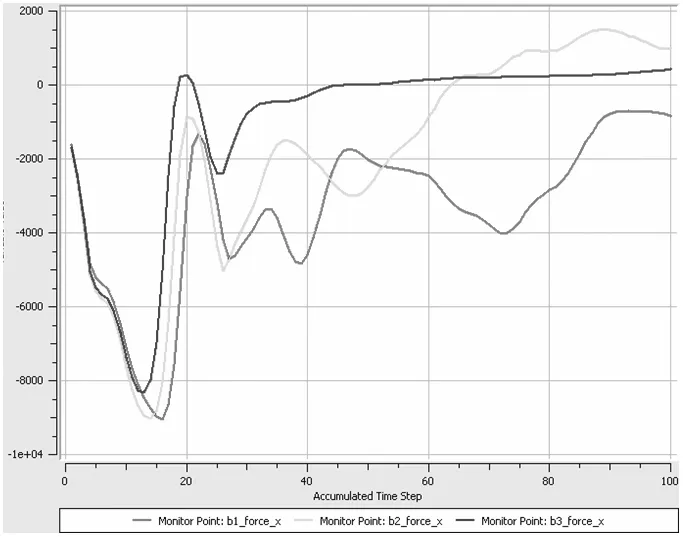
图2 防波板x方向受力曲线

防波板最大应力随时间变化的曲线如图3所示。由曲线可知，在前0.5s内应力变化幅度较大，之后变化幅度不大，在1.72s后应力变化趋于平缓，这与图2中曲线变化基本一致。防波板最大应力值出现在0.32s时刻，最大值为253.7MPa，防波板产生的最大应力值小于Q345的屈服极限345MPa，防波板的强度满足设计要求。

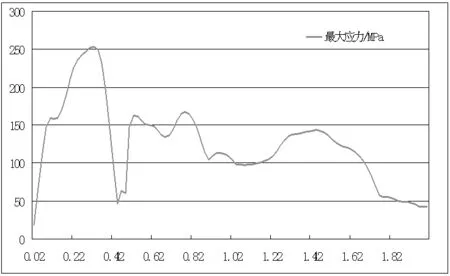
图3 防波板应力变化曲线

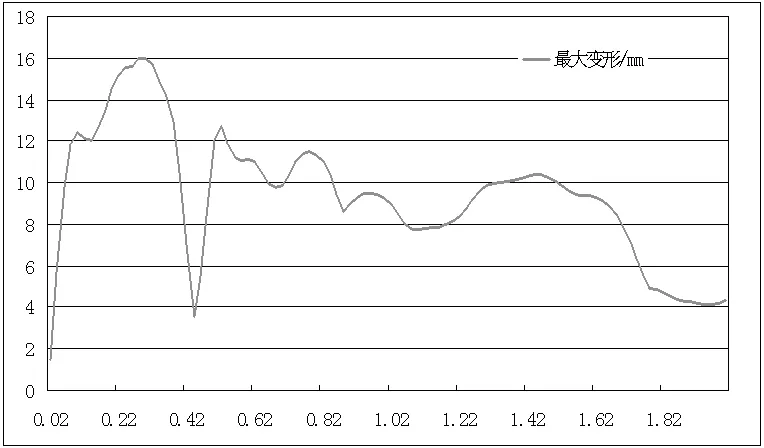
图4 防波板变形量变化曲线

测出防波板在流固耦合过程中每个时刻的最大变形量，观察最大变形量的变化情况，得到防波板最大变形量随时间变化的曲线如图4所示。对比图4和图3可以看出，防波板最大变形量变化曲线与最大应力变化曲线的变化形式几乎完全一致。从图4可知，在0.32s时刻防波板的变形最大，最大变形量为15.98mm，且出现最大位移的时刻与最大应力的时刻相同。防波板的最大变形量较大，对流场得影响较大，说明文中采用双向流固耦合计算方法是恰当的。

3 孔数、孔径及孔位的变化对防波板的影响

改变防波板的阻尼孔直径、位置和数量，此时防波板上有三个等直径的圆形阻尼孔，三个小孔呈等腰三角形排列，其直径为300mm，如图5所示。

图5 三阻尼孔防波板平面图

重新建立模型，设定相同的外界参数，进行仿真。将装有两种防波板的液面流动图进行对比（图6），图中左侧为装有两阻尼孔防波板的液面流动图，右侧为装有三阻尼孔防波板的液面流动图。可以看出，三阻尼孔防波板阻碍介质向后封头堆积的能力更强，隔离介质的效果更加明显，从而说明这种防波板抑制介质晃动的效果更加好。

图6 装有不同防波板的罐内液面流动图

由于介质晃动会对罐体产生冲击压力，防波板上阻尼孔数量和直径不同，罐体所受的冲击压力也不同。将三阻尼孔防波板在每个时刻受到的最大压力作为输出，可以得到安装两种不同结构防波板时罐体所受压力随时间变化的情况，如图7所示。此时三阻尼孔防波板的应力最大值为248.4MPa，小于材料的屈服极限，故此结构的强度满足设计要求。

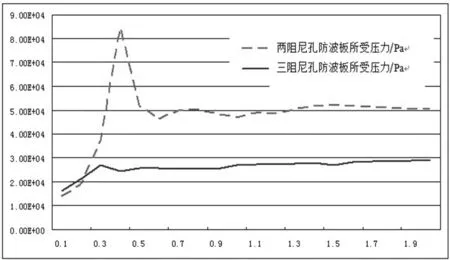
图7 安装不同防波板罐体手力变化曲线

从图7可以看出，采用两阻尼孔防波板时，罐体在前0.5s所受的最大压力会出现较大的波动，而后变化快速的趋于平缓，这表明在前0.5s内罐体内介质晃动较大，0.5s后晃动相对较为平缓。安装三阻尼孔防波板时，在0.4s时罐体所受压力达到最大，而后趋于平缓。相对于两阻尼孔防波板的受力变化曲线可知，安装三阻尼孔防波板时，罐体所受的压力明显小于两阻尼孔防波板，说明三阻尼孔的防波板的防波能力更好，这意味着减小阻尼孔的大小，增加阻尼孔的数量，改变阻尼孔的位置，可以提高防波板的防波性能，减小介质对罐体的冲击，这与理论分析的情况非常吻合[6]。

4 结束语

（1）采用流固耦合的方法分析介质和防波板间的相互作用，获得了防波板在罐车制动工况下的应力分布和变形情况，并校核了原防波板结构的刚度和强度。

（2）通过对比防波板上不同孔径、孔数、孔位对其性能的影响，为进一步优化提供了真实有效的数据。

［1］赵鹏.国外大型液罐车发展综述[J].专用汽车，1991（3）.

［2］向滔，陈国定，等.考虑流固耦合效应的油罐车瞬态应力分析[J].机械科学与技术，2010(08).

［3］王勖成.有限单元法[M].北京：清华大学出版社，2004.

［4］居荣初，曾心传，著.弹性结构与液体的耦联振动理论[M].北京：地震出版社，1983.

［5］Taylor G I.The pressure and impulse of submarine explosion waves on plates.In：Batchelor G Ked.The Scientific Papers of G.I.Ttaylor,Vol.2[J].Cambridge U-niversity Press,Cambridge，1963.

［6］乔维高.专用汽车结构与设计[M].北京：北京大学出版社，2010，9.