公路边坡稳定安全系数的参数敏感性分析
王斌 张力
(山西省闻合高速公路黄河大桥建设管理处,山西运城 044300)
边坡稳定性是边坡工程中最重要的控制因素和工程技术人员最关心的问题之一。然而实际工程中,由于边坡坡体材料本身的空间变异性,以及取样和实验过程中人和环境所造成的误差,使得实际试验参数具有明显的不确定性和随机性。目前,设计规范仍然采用确定性的设计思想,以此进行的设计必然与实际结构存在着较大的误差。
本文通过对影响边坡稳定的有关因素的分析得出不同参数取值的随机性对边坡稳定安全系数的影响。
1 基本原理
边坡稳定分析的常用方法包括极限平衡法、特征曲线法、极限分析法和数值分析法等。其中数值分析法克服了传统方法中对于滑裂面形状、土条间作用力等假设的缺陷且考虑了材料的应力应变关系使得计算结果的精确性得到了保证。
边坡工程数值分析常采用强度折减法评价边坡的安全稳定性。Bishop等将土质边坡稳定安全系数定义为沿整个滑动面的抗剪强度与实际抗剪强度之比,这也是实际工程中采用的计算方法。强度折减法的基本思想与此一致,均为边坡的强度储备安全度。其基本原理是将土体参数c,φ同时除以一个折减系数F,得到一组新的 c′,φ′值,即:

然后作为新的材料参数代入数值软件中进行试算,依据某种破坏判据判定系统是否进入极限平衡状态,经过多次迭代,边坡出现失稳时对应的F便为所求安全系数。
边坡失稳判据的选择对强度折减法的实现是很重要的,目前的边坡失稳判据主要有以下几类:
1)收敛性判据。
采用迭代不收敛作为边坡失稳的标志。
2)突变性判据。
以计算过程中关键部位发生位移突变,土体无限移动作为边坡失稳的标志。
3)塑性变形判据。
以广义塑性应变或者等效塑性应变从坡脚到坡顶贯通作为边坡破坏的标志。本文综合上述三种判据评价边坡的稳定性。
在进行边坡稳定性分析时,通常将土体假设成理想弹塑性体,本文选用摩尔—库仑屈服准则进行稳定性分析。
2 安全系数参数敏感性分析
文中采用1987年澳大利亚计算机应用协会(ACADS)对澳大利亚所使用的边坡稳定分析程序进行的调查评比考核题中的1(a)作为算例:一均质边坡,其尺寸见图1,其中土体重度 γ=20 kN/m3,弹性模量 E=10 MPa,泊松比 μ =0.25,粘聚力 c=3.0 kPa,内摩擦角 φ =20°(参考结果:简化 Bishop条分法为0.993,Janbu 法为 0.978,裁判答案 1.000)。
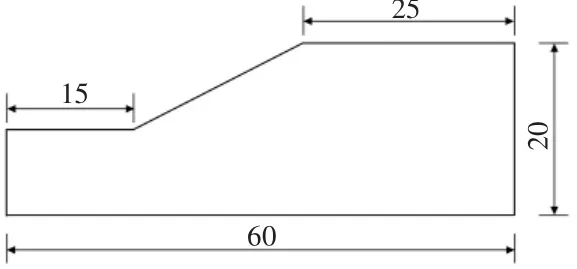
图1 边坡尺寸
根据张鲁渝、郑颖人等建议,建模时采用坡脚至左端边界距离为坡高的1.5倍,坡顶到右端边界距离为坡高的2.5倍,上下边界距离为坡高的2倍。
边坡问题为平面应变问题,根据上述建议建立如图2所示的准三维模型,极差分析数据见表1。
模型采用2 421个网格点,9 642个单元格。边界条件取为:左右边界x,z向受约束,下边界x,y,z向受约束,其余为自由边界。采用摩尔—库仑模型计算出的安全系数为1.007 81,与裁判答案基本一致。最大不平衡力采样记录图见图3,坡肩x轴位移采样记录图见图4,水平方向位移图见图5,最大位移出现在坡脚,坡顶坡脚位移贯通,剪应变率云图见图6。
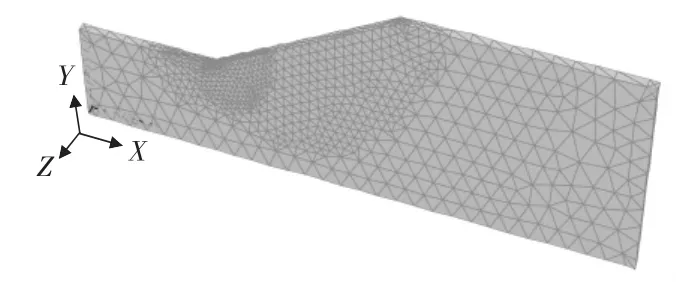
图2 准三维模型
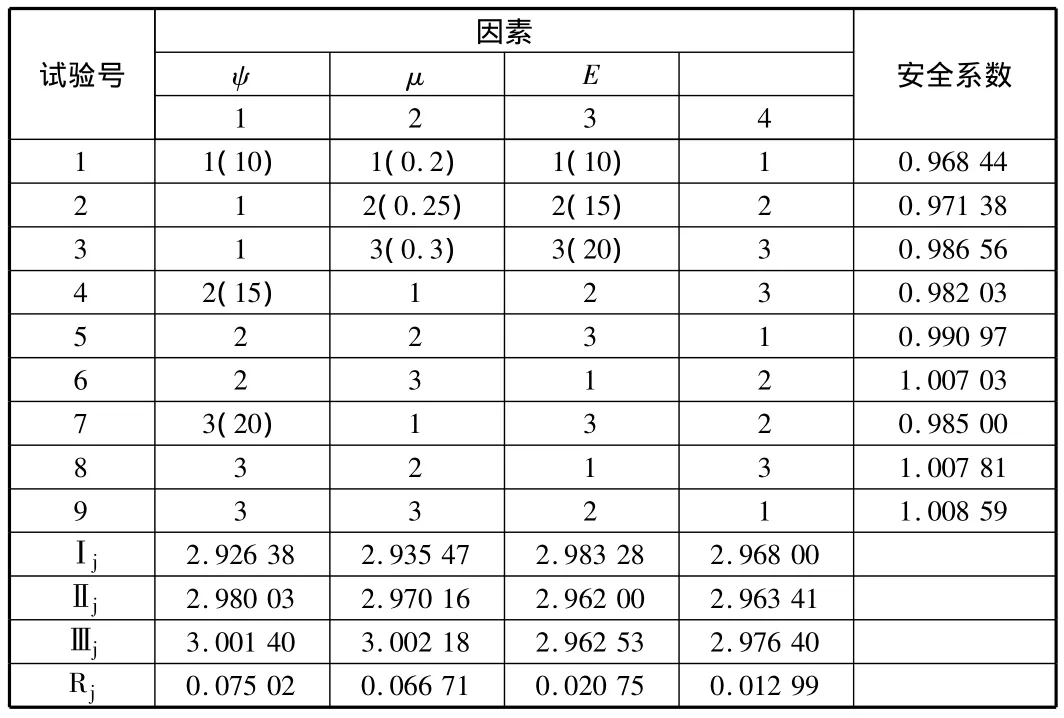
表1 极差分析数据表
边坡问题属于多因素多水平问题,本文选择土体的剪胀角、弹性模量和泊松比作为3个因素,各个因素选择三个水平,通过构造正交试验进行参数敏感性分析(见表2)。根据工程中常用的取值:对弹性模量E分别取10 MPa,15 MPa,20 MPa,对泊松比μ 分别取 0.2,0.25,0.3,剪胀角在 0 < ψ < φ 范围内分别取 10°,15°,20°。
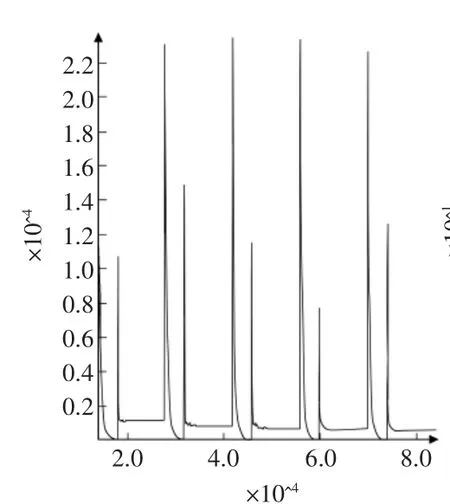
图3 最大不平衡力采样记录图

图4 坡肩x轴位移采样记录图
由于 F0.05(2,2)=19 且 Fψ=96.695 82 > 19,Fμ=25.651 04>19,故因素ψ,μ作用显著,E的作用不明显。这与极差分析的结果一致,且安全系数随着剪胀角的增大逐渐增大。
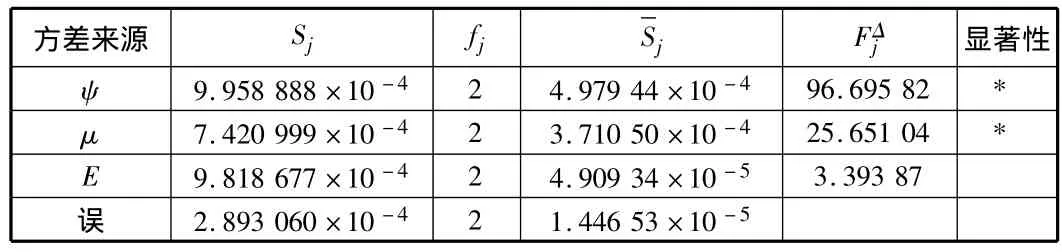
表2 正交试验方差分析表

图5 水平方向位移图

图6 剪应变率云图
3 结语
1)与传统方法极限平衡法相比,运用数值模拟手段基于强度折减法对边坡进行稳定性分析,可得到边坡坡体内各单元的应力应变图,能够更详细地了解边坡内应力应变的变化规律,为边坡后期治理方案的选择及设计提供可靠的理论依据。
2)通过运用正交试验方法得出各参数对边坡稳定安全系数的影响程度,能够为工程分析者提供一定的参考依据。
[1]吴 明,博旭东,刘 欢.边坡稳定分析中的强度折减法[J].土工基础,2006,20(1):49-52.
[2]张鲁渝,郑颖人,赵尚毅,等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003(1):21-27.
[3]栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,24(4):644-652.
[4]周翠英,刘祚秋,董立国,等.边坡变形破坏过程的大变形有限元分析[J].岩土力学,2003,24(4):644-652.
[5]关立军.基于强度折减的土坡稳定分析方法的研究[D].大连:大连理工大学,2003.
[6]李旭东.FLAC3D在边坡稳定分析中的应用[J].中国水运,2008,8(4):77-79.
[7]陈祖煜.土质边坡稳定分析原理方法程序[M].北京:中国水利水电出版社,2003.

