A－SMGCS航空器动态最优滑行路径规划研究＊

王 翀 汤新民 安宏锋

（南京航空航天大学民航学院 南京 210016）

0 引 言

基于航空运输业的发展及运营要求，ICAO提出了建设先进场面引导与控制系统的构想，即A－SMGCS［1］.其中，为场面航空器指定合适路由是实现A－SMGCS的前提和关键.

机场场面的动态路由规划要求保证进出港航班在滑行过程中按最短路径连续滑行，并且不能发生对头相遇.目前主要有两类研究思想：（1）在传统寻优算法思想基础上引入时间要素，将其应用到动态最优路径寻优中来［2－4］；（2）根据机场交通建立规划模型［5］和网络模型［6］，或建立包括机型和安全间隔等因素的混合整数线性规划模型［7］.将Petri网运用于路径规划方面，一些学者将无向交通网转成Petri网，再定义相关规则，求解最短路径［8］，并引入“时间库所”等［9］，但没有考虑机场场面动态因素.

本文根据机场场面结构建立场面活动模型及运行控制规范，引入关键事件轨迹等概念，求解基于场面全局最优的航空器规划路径.经计算机仿真验证，可以较好的满足机场高负荷条件下对实时性的需求.

1 机场场面结构建模与静态路径规划

机场场面交通系统是由航空器和道路、跑道、停机坪网络组成的复杂系统，分别对静态对象和运动对象建模是场面路径规划的基础［10］.本文以成都双流国际机场为例，建立符合机场场面物理特性和活动规则要求的场面活动模型.

定义1 场面活动模型定义为赋时库所Petri网TPN＝｛P，T，Pre，Post，m，Γ｝.式中：库所集P为航空器所处滑行段区域；变迁集T为航空器（托肯）所处的区域与下一区域的边界集L；Pre与Post分别表示P与T的前向和后向关联关系；m为场面各库所内的航空器分布向量.Γ为航空器a在某滑行段的平均滑行时间，由滑行段长度d（p）和航空器a的平均滑行速度va（p）求解，即：Γ（a，p）＝d（p）／va（p）.机场场面活动模型需满足以下规则.

规则1 若航空器可通过交界线l双向通行，则有Pre（pi，t）＝1∧Post（pi，t）＝1，此时场面活动模型并非纯网，为了避免这种情况的出现，需要将2个子区域的交界映射为2个变迁.

规则2 场面航空器所在滑行路段改变，需更新场面状态标识向量m.假设第k架航空器位于允许活动子区域内，以第i元素为1的n维单位向量ei标识第k架航空器的状态.假设场面内有na架航空器活动，则场面状态标识向量

图1 机场场面活动模型

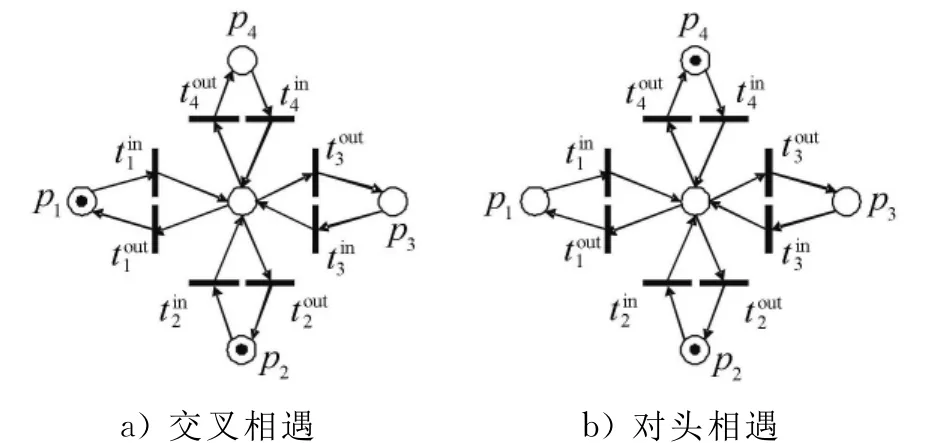
图2 航空器交叉和对头两种冲突

2 机场场面运行控制规范

2.1 场面活动优先规范

定义3 场面活动优先规范.场面活动模型状态演变过程中，变迁集合之间优先激发顺序关系可采用二元关系集Q定义：Q：T×T，若（t1，t2）∈Q，则表示当t1，t2∈Fe（m）时，t1优先于t2.定义航空器在交叉口相遇的二元关系集为QC.

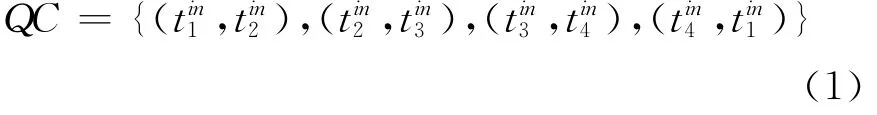
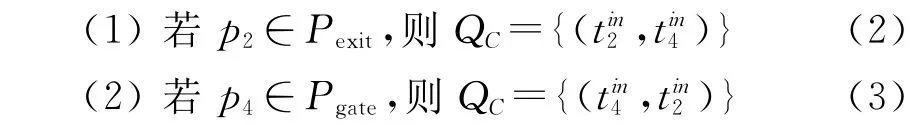
3）相向滑行的航空器可能在某一航段发生对头冲突.设对头路径πD＝（p1，…，pi，pj，pk，…，pn），航空器 A 由p0（A）向pn＋1（A）滑行，航空器B由p0（B）向pn＋1（B）滑行；则航空器 A、航空器B的可能冲突路段构成子Petri网系统＝ （PD，TD，PreD，PostD，mD，ΓD），见图3.

图3 对头路径的Petri网表示

定义二元关系集：QD：TD×TD，为TD中已激发变迁集合为未激发变迁集合，则

定义4 优先使能.设∃ti，tj∈Se（m），若存在二元关系集Q 使得（ti，tj）∈（QC∪QD），则称使能变迁集合ti为优先使能变迁集，记作Fe（m）.

2.2 场面活动禁止规范

定义5 状态禁止规范.场面活动模型状态演变过程中所禁止状态可描述为标识的加权和不超过某一上限的不等式组.

根据场面管制规则对场面滑行的航空器建立如下的约束条件.

1）航空器在跑道上滑行时不允许其他航空器进入跑道，该规范可描述为

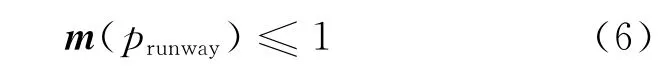
2）当跑道进近方向上有即将进入着陆的航空器，则其他航空器只能在跑道外等待，否则可进入跑道或穿越跑道，假设papproach为进近着陆库所，则该规范可描述为

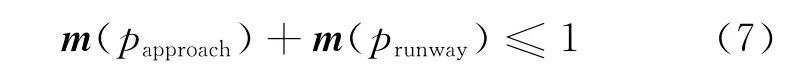
3）航空器在地面滑行时必须保持安全间距.为保证安全距离，每个库所pi内只允许一架航空器，该规范可描述为

定义6 约束使能.给出场面状态禁止规范后，可给出约束使能的概念，若∃t∈Fe（m），变迁t激发后满足状态禁止规范，则称变迁t满足约束使能，在标识m下约束使能变迁集记作Ce（m）.

3 基于Petri网动态滑行路径规划

动态路径规划的可行解集从预先规划的静态路径集合∏s中提取.∏s由求解K最短路径的相关理论［11］得到，并可据管制员经验选择c条常用滑行路径构成.

本文借鉴“先到先服务”的思想［12］，仅为进场航空器规划路径，并根据规划路径动态调整场面其他航空器的滑行时间.

3.1 动态路径规划目标函数的确定

定义7 滑行临界时刻向量.在场面活动模型∑＝（P，T，Pre，Post，m，Γ）内，某航空器ai沿由n段活动区域组成路径π（ai）滑行.航空器ai进入活动区域pk（pk∈π（ai））时刻为EFTk（ai），离开pk段预计时刻为 PLFTk（ai），PLFTk（ai）＝EFTk（ai）＋Γ（ai，k）.离 开 pk的 实际时刻为LFTk（ai），则三元组 CTSk（ai）＝（EFTk（ai），PLFTk（ai），LFTk（ai））构成航空器ai在区域pk的临界时刻状态（critical－time－state）.航空器ai在路径π（ai）各段上的时间状态标识构成时间状态向量［CTS1（ai），CTS2（ai），…，CTSk（ai），…，CTSn（ai）］.

定义8 关键事件轨迹.关键事件轨迹定义为二元组（λ，m）构成的序列〈Λ，M〉＝〈（λ0，m0），（λ1，m1），…，（λi，mi），…〉，其中m 为机场场面状态标识向量，λi为场面航空器的分布从机场场面状态标识向量mi－1变化为mi的瞬时时刻.

3.2 动态滑行路径规划算法

3.2.1 动态路径规划算法初始条件 关键事件轨迹反映了场面状态变化的时刻.若能求出场面运行的完整关键事件轨迹〈（λ0，m0），（λ1，m1），…，（λi，mi），…（λe，me）〉，即可求出场面各航空器新的时间状态向量及目标函数.见图4.

图4 动态路径规划算法

设当前为航空器a规划路径π（a），已知a进入场面时刻为TOA（a），场面上已存在的N架航空器分布向量为m0，即（λ0，m0）＝（TOA（a），m0），则初始关键时刻序列〈Λ，M〉＝〈（λ0，m0）〉.

此刻，场面任意航空器ai（包括a）在其滑行（规划）路径π（ai）第pi段滑行，离开pi预计时刻为PLFTpi（ai），场面N＋1架航空器构成初始目标序列〈P，PLFT〉＝〈（p1（a1），PLFTp1（a1）），（p2（a2），PLFTp2（a2）），…，（pN＋1（aN＋1），PLFTpN＋1（aN＋1））.

3.2.2 动态路径规划算法 动态路径规划算法是由初始条件推算场面关键事件轨迹、各航空器当在π（a）下的时间状态向量及目标函数Z（π）的过程.算法的结束条件为当前规划航空器a到达目的库所pend（a）.其流程图如图4所示.

图4中，若航空器ai在PLFTpi（ai）满足tpi（ai）∈Ce（mk），场面活动模型状态改变，更新相关序列及目标函数，规则如下：

1）更新关键事件轨迹〈Λ，M〉：

2）更新目标序列〈P，PLFT〉 PLFTpi＋1（ai）＝λk＋1＋Γ（ai，pi＋1），航空器ai更新为（pi＋1（ai），PLFTpi＋1（ai））；∀PLFTpj（aj）∈ PLFT 且PLFTpj（aj）＜PLFTpi（ai），令（aj）＝λk＋1，即（pj（aj），λk＋1）.

3）更新航空器ai滑行临界时刻向量 航空器ai离开当前段时刻和进入下一段时刻相同，即LFTpi（ai）＝EETpi＋1（ai）＝λk＋1，航空器ai离开下一段预计 时刻PLFTpi＋1（ai）＝λk＋1＋Γ（ai，pi＋1）.

4）更新目标函数Z（π） 航空器ai在pi段等待时间WTpi（ai）＝LFTpi（ai）－PLFTpi（ai），故Z（π）′＝Z（π）＋WTpi（ai）ξi，ξi为航空器ai的等待权重.

遍历当前规划航空器a的静态路径预选库，从中找出路径πα，使得Z（πα）最小即可.

表1 进离港航空器静态预选路径

4 态滑行路径规划研究案例

为验证航空器动态滑行路径规划方法的有效性，结合场面活动模型进行计算机仿真.

设预选路径数s＝3，对个进离港求得预选路径集合Πs，见表1.其中：App为进近库所；Gx为GateX.

根据航空器进离港时间的先后顺序，对航空器动态行为进行仿真.利用动态路径规划模型，为每架航空器计算最优路径及滑行总时间.假设每架航空器仿真5次，每次仿真结束再次加入仿真队列，仿真结果见表2.

由表2可见，2种方法规划的路径均存在一定等待时间，这是依据管制规则避免与其他航空器冲突而实施等待造成的.经过动态路径规划，滑行时间虽略为增加，但总时间降低了，这是由于动态路径规划充分考虑了场面的动态变化，避开了容易发生拥挤的路段，减少了航空器等待时间，对于航班量越大的机场，其优化效果越明显.

表2 静态路径和动态路径规划结果比较

5 结束语

本文建立了基于Petri网的机场场面活动模型，并根据ICAO－9830文件定义了场面活动控制规范.以静态规划路径的结果为可行解集，研究了以全局等待时间权值最少为约束目标的动态最优规划路径算法.由于本文主要以单跑道机场为研究对象，未来的研究重点偏重于该算法在多跑道的大型机场的应用，并将滑行路径规划与冲突解脱相结合，为航空器的滑行实施精确的规划与引导.

［1］ICAO.Advanced surface movement guidance and control systems manual［R］.ICAO－9830，2004.

［2］丁一波，靳学梅，杨 恺.浅析A－SMGCS中的自动路由规划技术［J］.空中交通管理，2009（11）：16－18.

［3］刘长有，丛晓东.基于遗传算法的飞机滑行路径优化［J］.交通信息与安全，2009，27（3）：6－8.

［4］HESSELINK H H，PAUL S.Planning aircraft movements on airports with constraint satisfaction［R］.National Aerospace Laboratory，1998.

［5］MARIN A G，CODINA E.Network design：taxi planning［J］.Annals Operation Research，2008，157（1）：135－151.

［6］BAIK H，SHERTALI H D，TRANI A A.Time－dependent network assignment strategy for taxiway routing at airports［J］.Transportation Research Record，2002：70－75.

［7］RATINAM S，MONTOYA J，JUNG Y.An optimization model for reducing aircraft taxi times at the Dallas FortWorth International Airport［C］／／26th International Congress of the Aeronautical Sciences，Anchorage，2008：1－14.

［8］张 威，谢晓妤，刘 晔.基于Petri网的机场场面路径规划探讨［J］.现代电子工程，2007，4（1）：59－61.

［9］黄圣国，孙同江，吕 兵.运输网络的最短有向路Petri网仿真算法［J］.南京航空航天大学学报，2002，34（2）：121－125.

［10］汤新民，王玉婷，韩松臣.基于DEDS的 A－SMGCS航空器动态滑行路径规划［J］.系统工程与电子技术，2010，32（12）：2669－2675.

［11］李成江.新的K最短路算法［J］.山东大学学报：理学版，2006，41（4）：40－43.

［12］王 维.机场飞行区管理与场道施工［M］.北京：人民交通出版社，2007.