若干合成图的星全染色＊

王晓琦 田双亮

（西北民族大学数学与计算机科学学院 兰州 730030）

0 引 言

本文所考虑的图G均为有限无向简单图，用V（G），E（G）分别表示图G的点和边的集合.并用Δ（G）表示G的最大度.

定义1［1］简单图G和H 的合成图是指具有顶点集V（G）×V（H）的简单图G［H］，它的顶点（u，v）和另一个顶点（u′，v′）相邻当且仅当或者uu′∈E（G），或者u＝u′且vv′∈E（H）.

合成图G［H］也可看成是若干个同构于H的不相交图关于G的等广义联图［2］.特殊地，当G为n阶完全图Kn，合成图Kn［H］也可称为n阶完全图Kn与H 的等多重联图［3］.

定义2 图G的k－全染色是从V（G）∪E（G）到S＝｛1，2，…，k｝的一个映射σ，使得G 中没有相邻顶点或边具有相同的像，且每个顶点与其关联边有不同的像.使G存在k－全染色的最小k值称为G的全色数，记为χT（G）.

定义3 图G的一个k－全染色σ被称为k－星全染色，如果图G中任意长为2的路的顶点和边染不同颜色.即G中任意星上的顶点与边染不同的颜色.使G存在k－星全染色的最小的k值称为G的星全色数，记为χst（G）.

由定义3，容易得到以下引理：

引理1 对任意n阶简单图G，n≥3，有2Δ（G）＋1≤χst（G）≤n＋χ′（G）.式中：χ′（G）为G的边色数.

引理2 对G的任意子图H，有χst（H）≤χst（G）.

引理3 若G的直径D（G）≤2，则在G的任一星全染色中，G的不同顶点必染不同的颜色.

在后面的讨论中，需用到以下引理：

引理4 偶图G的边色数等于Δ（G）.

文献［2］研究了一些等广义联图（或合成图）的Mycielski图的星全染色，文献［4－7］研究了完全图与完全多部图的Mycielski图，以及轮，扇与路的广义Mycielski图的星全染色.本文将研究n＋1阶轮，扇，星与m阶简单图的合成图的星全染色.文中未加说明的术语及符号可参见文献［1］和［4］.

1 主要结果及其证明

设简单图G与H 的顶点集分别为V（G）＝｛ui｜i＝0，1，…，n｝与V（H）＝｛vi｜i＝0，1，…，m－1｝.在G［H］中，记wij＝（ui，vj），并令Vi＝｛（ui，vj）｜j＝0，1，…，m－1｝.由合成图的定义，G［H］可表述为若干边不交的子图之并，即

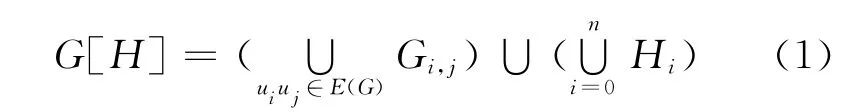
式中：Gi，j为以（Vi，Vj）为二分类的完全偶图，Hi表示以Vi为顶点集且同构于H 的简单图.显然，在G［H］中，有Gi，j≅Km，m，且Hi与Hj是不相交的，其中i≠j，i，j＝0，1，…，n.下面研究当G 为n＋1阶轮Wn，扇Fn，或星Sn，且H 为m 阶特殊图时合成图G［H］的星全染色.

设n＋1阶轮Wn的顶点集与边集分别为

其中ui＋1的下标取模n，n≥4.

显然，n＋1阶扇Fn与星Sn可由Wn删去若干条边得到.

引理5 设G为n阶简单图，n≥5.若Δ（G）＝2，则G存在n－星全染色，使得G的不同顶点染不同的颜色.

证明 不妨假设G是简单连通图.因Δ（G）＝2，所以G为n阶圈或路.仅证明当G为n阶圈时引理结论成立，当G为n阶路时，可类似证明.

设G为n 阶圈且G＝v0e0v1e1…vn－1en－1v0.设颜色集合为S＝｛0，1，…，n－1｝.现在定义如下一个从V（G）∪E（G）到S的映射σ：

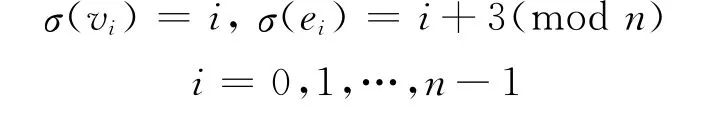
显然σ为G的n－星全染色，且使得G的不同顶点染不同色.因此，引理结论成立.

定理1 设G为n＋1阶轮，扇，或星，且H为m 阶简单图，其中n≥4，m≥5.若Δ（H）＝2，则χst（G［H］）＝（2n＋1）m.

证明 记G＊＝G［H］.显然，G＊的直径不超过2，即D（G＊）≤2.由引理3，在G＊的任一星全染色中，G＊的不同顶点必染不同的颜色，又因｜V（G＊）｜＝（n＋1）m，所以至少需要（n＋1）m 种颜色.另一方面，对任意边uv∈E（Gn，i），i＝0，1，…，n－1，每一顶点ω∈V（G＊）＼｛u，v｝均与u或v相邻，所以在G＊的星全染色σ中，的每一边不能与G＊的任一顶点染相同的颜色.又因为是最大度为mn 的偶图，由引理4知，）＝mn.所以，χst（G＊）≥（n＋1）m＋mn＝（2n＋1）m.又因为Sn⊂Fn⊂Wn，由引理2，χst（Sn［H］）≤χst（Fn［H］≤χST（Wn［H］）.因此，欲证χst（G［H］）≤2（n＋1）m，仅需证明当G＊＝Wn［H］时，G＊存在（2n＋1）m－星全染色.

设颜色集合为S＝A∪B，且｜S｜＝（2n＋1）m，｜A｜＝ （n＋1）m，｜B｜＝nm.其中：A ＝；B ＝；｜Ai｜＝m；｜Bj｜＝m.现在分3步构造G＊的染色σ：在式（1）中，首先用Ai中的m种颜色对Hi进行顶点染色，使得不同顶点染不同色，i＝0，1，…，n.其次，对i＝0，1，…，n，因为Hi≅H及Δ（H）＝2，由引理5，可用Hi的顶点颜色对Hi的边进行染色，使其成为Hi的m－星全染色.最后，用B中mn种颜色对∪uiuj∈E（G）Gi，j进行正常边染色.具体地，因为Gi，j≅Km，m，由引理4，可用Bi中的m 种颜色对Gn，i进行正常边染色，用Bi＋2中的m种颜色对Gi，i＋1进行正常边染色，其中Bi＋2的下标与Gi，i＋1的第二个下标i＋1取模n，其中i＝0，1，…，n－1.

容易看出，以上染色σ是G＊的（2n＋1）m－全染色，且在σ中，∪uiuj∈E（G）Gi，j的每一边所染颜色与任意顶点所染颜色均不相同，并满足G＊的不同顶点染不同的颜色.同时，σ限制在每一个Hi上均为Hi的星全染色，且不同的Hi所用的颜色集合不同.又因Hi与Hj是不相交的，其中i≠j，i，j＝0，1，…，n，所以在σ中，G＊的任意长为2的路的顶点和边均染不同颜色，即σ是G＊的（2n＋1）m－ 星全染色.因此，χst（G＊）＝ （2n＋1）m.

定理2 设G为n＋1阶轮，扇，或星，若H满足χ′（H）＝Δ（H）＝m－1，其中n，m≥4，则χst（G［H］）＝2（n＋1）m－1.

证明 记G＊＝G［H］.由已知及引理1可得

由上式可知，若能证明χ′（G＊）≤（n＋1）m－1，则定理结论成立.又因Sn⊂Fn⊂Wn，由合成图的定义，有G＊⊆Wn［H］.因此，仅需证明当G＝Wn时，G＊存在（（n＋1）m－1）－正常边染色.

假设G＝Wn，并设颜色集合S＝B∪C，且｜S｜＝（n＋1）m－1，｜B｜＝mn，｜C｜＝m－1，其中B＝，且｜Bj｜＝m，j＝0，1，…，n－1.

现在构造G＊的边染色σ：在式（1）中，首先用B中的nm 种颜色对 ∪uiuj∈E（G）Gij进行正常边染色，染色方法与定理1证明中的第三步相同.其次，因χ′（H）＝m－1，所以可用C中的m－1种颜色对每一个Hi进行正常边染色.

显然，以上染色σ是G＊的（（n＋1）m－1）－正常边染色.因此，定理结论成立.

2 结 论

由定理2可直接得到以下结论：设G为n＋1阶轮，扇，或星，其中n≥4.若H满足以下条件之一：（1）H 为m 阶轮，扇，或星，其中m≥4；（2）H为偶阶完全图，则χst（G［H］）＝2（n＋1）m－1.

［1］BONDY J A，MURTY U S R.Graph theory with application［M］.New York：American Elsevier，1976.

［2］田双亮.等广义联图的Mycielski图的星全染色［J］.山东大学学报：理学版，2009，45（6）：23－26，34.

［3］田双亮，陈 萍.若干多重联图的边染色［J］.南开大学学报：自然科学版，2007，40（3）：27－30.

［4］YAP H P.Total colorings of graphs［M］.New York：Springer Verlag，1996.

［5］李沐春，强会英，张忠辅.完全图和完全多部图的Mycielski图的星全染色［J］.福州大学学报：自然科学版，2009，37（2）：180－183.

［6］强会英，李沐春，徐保根，等.轮和路的广义Mycielski图的星全染色［J］.兰州理工大学学报，2008，34（4）：145－147.

［7］强会英，李沐春，张忠辅.星图和扇图的广义Mycielski图的星全染色［J］.江西师范大学学报：自然科学版，2009，33（3）：306－308.