城市交通拥堵背景下的出租车管制效应分析

陈文强，吴群琪

（长安大学经济管理学院，陕西西安710064）

相对于城市其他公共交通运输系统，出租车具有迅速、方便、私密、可及性高和营业时间长等特性，而且可以免除私家车必须自己驾车、停车问题。显然，出租客运是城市公共交通的重要组成部分，在绝大多数城市中也是不可或缺的组成部分。随着我国城市化进程加快，城市出租车行业规模和质量都不断得到扩大和提升，但发展过程中也存在一系列的问题和矛盾，有时还因此导致群体事件发生，成为影响社会的不稳定因素。解决问题必须找寻问题产生的原因，基于此，本文研究出租客运行业特性，评析行业管制效果。分析出租车行业的管制效果，不能撇开公共交通这个重要背景，尤其是那些道路资源紧张、时间成本较高的特大城市，更是如此。基于此，本文重点研究城市交通拥堵大背景下的出租车管制效应。

1 出租车行业市场特性与管制

从经济范畴层面分析，出租客运行业有几点显著的特征。其一，资源的约束性[1]。相对于一般经济资源，任何城市的交通资源都是非常有限的，快变的交通需求和慢变的交通供给特点，决定了出租车的供给数量是不可能随需求增长而快速增加，因为承载出租客运的关键资源（道路资源）的供给不具有一般市场竞争领域资源随需求变化而自由流动的条件。其二，消费的约束性[2]。普通商品可摆在柜台上供消费者选择，消费者选择普通商品的时空约束不明显，此时购买或彼时购买、此地购买或彼地购买往往有充分的选择余地。城市居民出行具有极强的随机性，而且受到出行时空和供给的严格约束，消费者在什么时候、要到什么地方去往往没有选择余地，可供选择的服务通常是唯一的。其三，交易的一次性。运输生产最典型的特征之一是生产过程与消费过程的统一，由于服务过程与消费过程统一，交易过程又是随机发生的，所以出租车交易具有一次性特点；其四，服务的非后效性。出租车司机与乘客之间具有的“一次性”交易特点和消费的约束性赋予了出租车服务行为“优劣”的非后效性特征。如果碰到“优”的经营者，则属运气好，若碰到“劣”的，则自认倒霉。这种服务行为“优劣”的非后效性特征必然导致市场的劣化，因为优者必然要有“优”的投入，但却不一定得到“优”的回报，而“劣”者以其低廉的投入可能比优者获得更多的回报[3]。综上所述，出租车市场的非竞争市场特性和服务的非后效性决定了优胜劣汰的市场竞争规则在这一领域难以充分发挥作用，达不到优化资源配置的效果，需要外力介入[4]。

出租车行业特性决定了完全由市场左右出租车供给是不现实的，适当的政府管制在一定程度上是必要的。近几年，我国出租车行业矛盾突出，国内外探讨出租车管制的文献备受关注。这些文献关注的重点集中在管制行为下的出租车服务模型与经济学解释。其中比较著名学者有Douglas（1972），Shreiber（1975，1981），Cairns和Liston-Heyes（1983），Yang等（1998，2002，2003）[5-10]。这些学者提出的出租车管制效应模型大部分是沿用Douglas（1972）和Beesley与Glaister（1983）提出的分析性经济模式框架。然而此模型框架中并未考虑城市交通拥堵等外部性特征对出租车服务管制效应的影响，而且有限的城市道路资源和对出租车交通拥挤外部性的考虑，从来就是出租车行业管制的一个重要理由。例如，郭玉闪（2005）指出北京出租车占路面交通量的30%～40%，平时白天空驶率约为37%，晚上空驶率为40%～50%，这样便无效占用了道路的面积。如果出租车空驶率能减少20%的话，整个交通量就能够减少8%[11]，这样可以有效减少交通拥堵压力。因此出租车市场的管制分析需要综合考虑交通拥堵致因和空车率的影响，本文基于此研究出租车政府管制效应。

2 模型的基本框架

本文模型是在Yang H.（2003）[10]提出的模型基础上修改而得到的。设出租车运价结构由3部分组成：起步价，公里价和延迟运价。用s=0,1,...,23来表示一天中的24个小时，用来表示第s小时中一个给定的城市出租车服务起步价（元），表示第s小时中出租车服务距离运价（元/公里），表示第s小时中出租车服务延迟运价（元/分钟），L表示平均行驶里程（公里），Ts表示第s小时中平均每旅次耗时（分钟）；Ps表示第s小时中出租车平均服务价格；可以设，其中，ψ，ζ为外生变量，用来表示一天中不同时段单位运价和延迟运价的变化。由于和L是外生变量，可令表示出租车不堵情况下的运价。因此，Ps函数可以表示为

用Qs表示在第s小时中一个给定城市出租车服务需求数量，同时也是成交量，设

其中：as是外生变量，用来表示一天中不同时段需求量的变化，可以规定as＞0；ws表示在第s小时内每个潜在乘客的平均等待时间；设g1,g2,g3分别为Qs的P，T，W偏导，有理由设g1＜0，g2＜0，g3＜0。

令N为路网上出租车的数量；Nsv表示在第s小时内某个时点空驶车的数量；NsO=N-Nsv表示在第s小时内某个时点载客车的数量；Nsn表示路网上除了出租车外的其他车辆数量；我们把出租车服务看成一个“生灭”过程[12]，用λ代表平均“出生率”，即载客车变成空车的平均速率；在交通拥挤状况比较严重的时段，每次服务的平均运行时间越长，λ越小。μ代表平均“灭亡率”，即空驶车变成载客车的平均速率。μ的大小与交通拥挤状况的好坏有关，交通拥挤越严重，μ越大。我们知道，乘客的等待时间ws取决于空车数目，空车数目又和λ成反比，与μ成正比。我们把过程Nsv看成是一个有限状态的生灭过程，其状态即是系统中空驶车数。

由生灭的马尔科夫性[13]可知

出租车平均载客行程时间不仅受旅客出行距离影响，而且还受路网上车辆密度的控制，因此Ts可以表示为

3 交通拥堵与管制效应

下面讨论交通拥堵背景下的出租车管制效应。

1）价格和数量管制（价格Pf，βt管制和数量N管制）对平均旅次耗时和旅客等待时间影响。

对式（4）进行简单计算，得

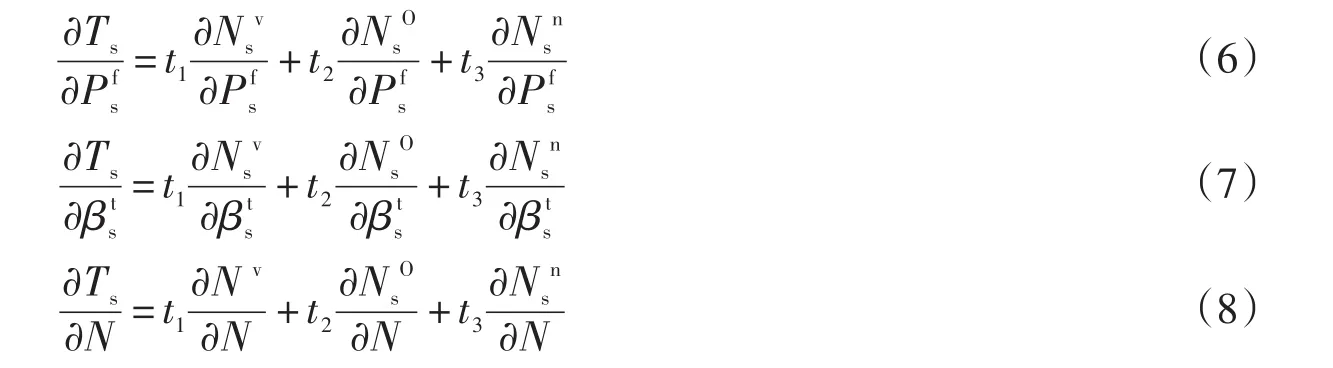
由式（5）（8）可知

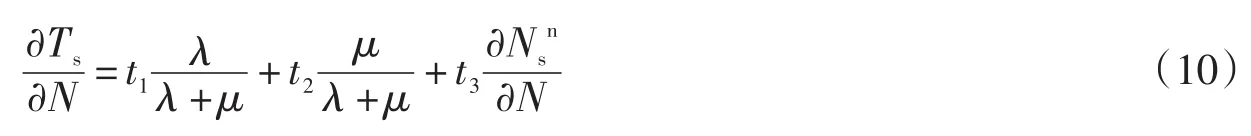
无论是空车还是载客车对交通流（行驶速度）的影响的边际效应是一样的，即t1=t2，因此（10）式可以写为

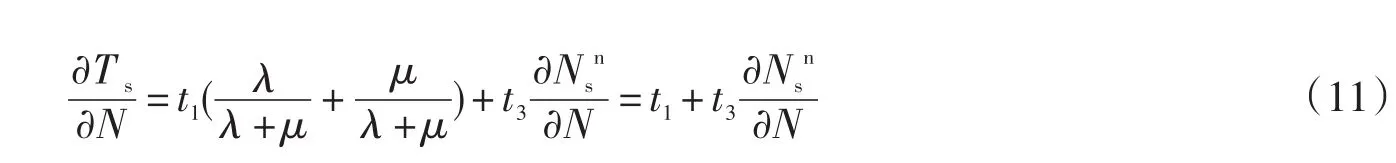
（12）式表明在某个小时内，出租车营运数量和每次运营的平均时间是正向相关的，也就是说出租车和其他车辆的增加加剧了交通拥挤程度，城市交通流速度降低，导致每次运营的平均时间Ts增加。Ts延长导致出租车“出行率”λ降低，我们知道，乘客的等待时间ws取决于空车数目，空车数目又和λ成反比，因此旅客等待时间ws增加，出租车服务需求转移，导致道路上其他车辆增加，这样城市会更加拥堵，陷入恶性循环中。

（13）式表明在某个小时内，出租车营运数量和每次运营的平均时间是正向相关的，也就是说此刻如果增加出租车数量（出租车增幅数量要大于其他车辆的减幅数量），就会加剧交通拥挤程度（交通流中出租车比重较大），城市交通流速度降低，使每次运营的平均时间Ts增加。

（14）式表明在某个小时内，出租车营运数量和每次运营的平均时间是反向相关的，也就是说出租车数量增加没有影响到城市整体交通流特性，由于出租车的实载率大于私家车实载率，出租车增幅数量小于其他车辆的减幅数量，城市道路上交通流量减少，流速速度增加，使每次运营的平均时间Ts减少。Ts降低导致出租车“出行率”λ增加，乘客的等待时间ws取决于空车数目，空车数目又和λ成反比，因此旅客等待时间ws减少。

2）价格管制和数量管制（价格Pf，βt管制和数量N管制）对出租车需求影响分析

对（1）式进行简单计算，容易得到

由式（9），（12），（13），（14）和 p1＞0 ，p3＞0 ，p3＞0 ，可知

对式（2）求偏导，得

结合（3）式，式（22），（23），（24）变换如下经过简单计算可知即出租车运价与出租车服务需求量成反向关系，这符合一般竞争市场规律。

由 as＞0，p1＞0，t1，t3＞0，g1＜0,g2＜0,g3＜0，w′＜0和式（26）可知，∂Qs∂N符号不定。令

简单计算得

以西安城市为例，2011年底西安市共有11 773辆出租车，私家车数量为907 386辆，主城区面积为400平方公里，假设这些出租车和私家车随机行驶在主城区内。假设每隔一段时间往西安主城区投放1 000辆出租车，共投放6次，状态分别为A-F，并利用VISSM软件模拟仿真，研究路段A高峰时刻交通状态相关问题。模拟结果见表1。

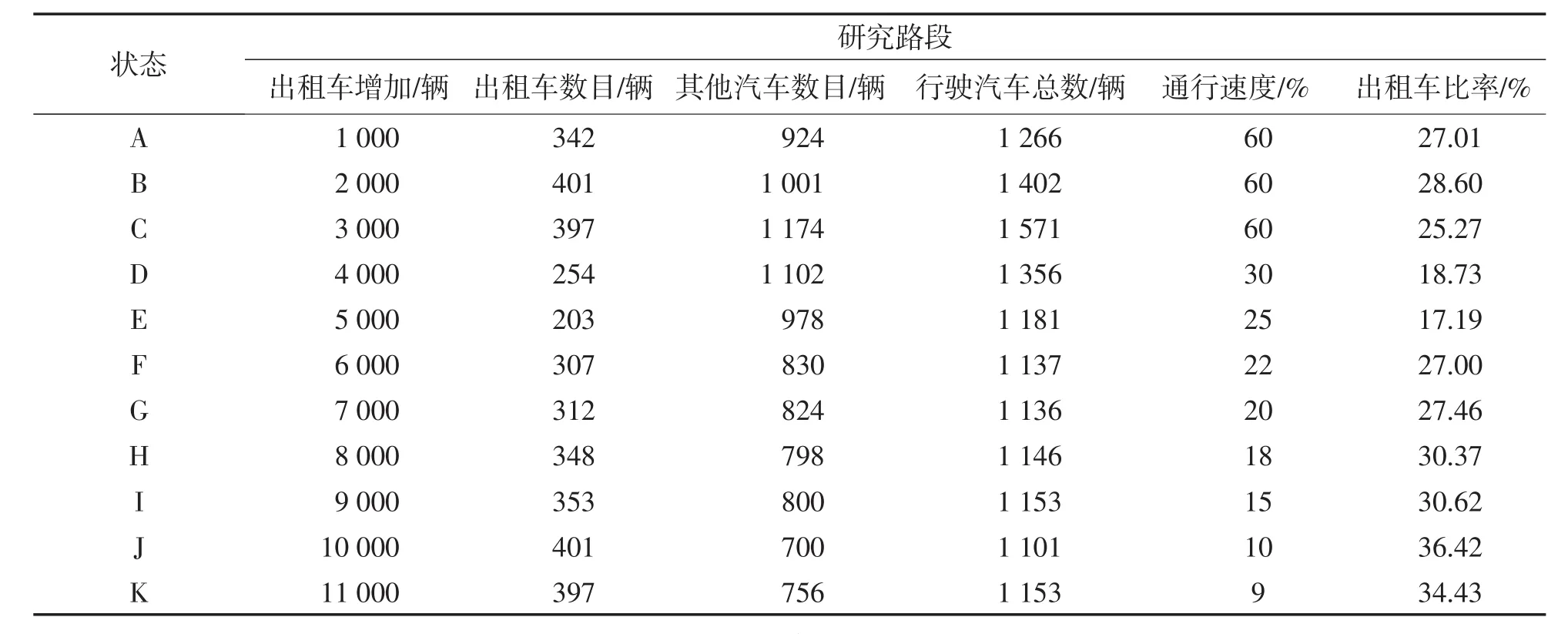
表1 不同投放比例下研究路段交通状态模拟结果Tab.1 Results of traffic state simulation in different delivery ratios

从表1可以看出，在前三个状态，出租车数量和其他汽车数量相对稳定，出租车流量占路面交通量在四分之一左右。当出租车数量增加到4 000辆时，高峰时刻路面交通拥挤程度明显增加，交通流速降低从（60 km·h-1减至20 km·h-1），路段出租车数量和出租车比例与前三个阶段相比都明显下降。随着出租车数量和私家车的增加，交通拥挤程度增加（t增加），车流的速度减慢（从60 km·h-1减至20 km·h-1），从而导致在单位时间内统计到的出租车数量减少。而当出租车增加到6 000辆时，出租车比率又上升到和状态A差不多的水平。从总体来看，出租车比率在17%～36%之间，与行车速度成反向关系。

将表1中的数据描绘成图形1，可以比较清楚地看出出租车占用路面交通量在不同状态段的变化。需要指出的是，为了能够在一张图中表示出所有数据的变化趋势，我们把所有状态段的交通速度乘以10，出租车比率都乘以了1 000。

从图1中我们可以清楚地看到，在第五个状态，也就是出租车增加5 000辆时，出租车比率降低，并且这种下降的趋势在后一个状态更加明显，之后才有所回升。可以看出，出租车比率呈现出明显的U型变化趋势。这是因为当增加出租车不足以影响交通流速时，出租车生灭率增加，统计到的出租车量就多，而当出租车增加至影响交通流速时，车速慢，生灭率很低，统计到的数量自然低，然而出租车数量增加至足够多时，意味着出租车数量于其他车辆比率增大。

图1 不同交通状态时出租车比率、车速和车辆数变化Fig.1 Taxi ratio，speed and number in different traffic conditions

4 结语

本文基于交通拥堵背景分析了出租车行业价格和数量管制效应，研究结果表明：

1）改善出租车运营系统的服务水平，不能仅靠增加出租车数量来保证，也要从改善城市的整体交通状况上综合考虑。另外，由于乘客的需求量是与出租车的收费标准有关的。因此，在城市交通状况趋于饱和的情况下，可以通过调整出租车的收费标准来调节乘客的需求量。

2）不同交通背景下，出租车行业制度选择应有所不同。如果城市出租车数量增加不足以影响整个城市交通效率时，出租车数量、运价由市场机制来调节，为最理想态；此时如果进行数量和价格管制将会造成旅客出行难、打车难问题，也是非法营运出租车大量存在的主要诱因；如果出租车增加会全面影响整个城市交通效率时，解除数量管制和价格管制后，将会造成更严重的拥堵，出租车运营系统的整体服务水平将下降，因此此刻必须进行政府管制。

[1] SHREIBER C.The economiac reasons for price and entry regulation of taxicabs[J].Journal of Transport Economic and Policy，1981，15（1）：102-131.

[2]吴群琪.出租客运的性质、地位和应有的管理模式[J].城市问题，2011，7（11）：84-88.

[3]吴群琪，陈文强.道路客运行业政府管制分析[J].交通企业管理，2009（4）：29-31.

[4]刘小兵.政府管制的经济分析[M].上海：上海财经大学出版社，2004：7.

[5] DOUGLAS G W.Price regulation and optimal service standards：The taxicab industry[J].Journal of Transport Economics and Policy，1972，6（2）：116-127.

[6]CAIRNS R D，LISTON-HEYES C.Competition and regulation in the taxi industry[J].Journal of Public Economics，1996，59（1）：1-15.

[7]YANG H，LAU Y W，WONG S C，LO H K.A macroscopic taxi model for passenger demand，taxi utilization and level of services[J].Transportation，1997，27（3）：317-340.

[8]YANG H，WONG S C，WONG K I.Demand-supply equilibrium of taxi services in a network under competition and regulation[J].Transportation Research，2002，36（9）：799-819.

[9] YANG H，YE M，TANG W H，et al.Modeling urban taxi services：a literature survey and an analytical example[J].Advanced Modeling for Transit Operations and Service Planning，2003，3（3）：257-286.

[10]郭锐欣，毛亮.特大城市出租车行业管制效应分析：以北京为例[J].世界经济，2007（2）：75-83.

[11]周晶，何建敏，盛昭瀚.城市出租车运营系统的随机分析[J].管理工程学报，2000，14（1）：63-66.

[12]贺振欢.用户出行费用综合更新自学习模型的研究[J].华东交通大学学报，2010，27（1）：12-16.