蒙特卡罗法在电力系统暂态稳定评估中的应用

叶国华，孔祥玉，孙 闻

（1.广东省粤电集团有限公司，广州 510630；2.天津大学智能电网教育部重点实验室，天津 300072；3.广东电网公司电力科学研究院，广州 510080）

电力系统暂态稳定性是指系统突然经受大干扰后，各个同步电机能否继续保持同步运行的能力。通常所考虑的扰动包括发生各种短路故障、切除大容量发电机或输电设备以及某些负荷的突然变化等［1］。在传统的暂态稳定性安全分析中，多采用确定性安全评估方法：电力工程师首先选择要分析的时间范围、负荷状况、网络结构和事故列表；然后确定最先违反系统运行状况标准的事故；最后再决定这些事故的解决方法。确定性方法由于计算结果物理意义明确，在电力系统安全经济分析中已得到了广泛应用［2，3］。

尽管确定性方法曾经取得了很大的成功，但由于只重视最严重、最可信的事故，计算结果显得过于保守。从运行的角度来看，现存的设备没有被充分利用；从规划的角度来看，造成不必要的重复建设。因此在电力系统的稳定性评估领域内，概率分析方法备受关注，并逐渐成为该领域研究热点［4，5］。

现阶段，国内外已有大量电力系统概率稳定性评估方面的研究，如文献［6］从随机变量、概率模型、概率算法以及特定场景下的暂态稳定评估等方面，回顾国内外对暂态稳定概率分析和风险分析的研究和现状，归纳各种分析方法的原理及优缺点，并探讨了暂态稳定性概率分析及风险分析的发展方向。文献［7，8］分别则介绍蒙特卡洛法的基本原理及其在电力系统可靠性评估中的应用，并从提高蒙特卡洛法收敛速度的方法、蒙特卡洛法与解析法的结合、蒙特卡洛法中负荷的处理等几个方面加以分析。

随着电力系统规模的扩大和运行环境的日益复杂，基于概率的暂态稳定评估计算对于电力系统的规划和运行具有越来越重要的意义。一方面，大规模电力系统的安全稳定评估计算量巨大，需要有很好的仿真处理方法；另一方面，工程实践中对评估的速度和精度的要求越来越高。研究提高基于蒙特卡罗方法的可靠性评估算法的计算效率，缓解甚至消除计算精度和速度之间的矛盾成为一项十分迫切的任务。

1 电力系统的概率性评估方法

1.1 概率性评估方法分类

电力系统的概率性评估方法主要分为两类，即解析法和蒙特卡罗模拟法。解析法的计算量随系统元件数的增加呈现指数增长，在电力系统规模越来越大的今天，一般只适合用于元件数目不多且元件故障有重大影响的系统。

蒙特卡罗方法又称统计试验方法或随机抽样技术，在使用蒙特卡罗法进行可靠性评估时，首先要建立一个概率模型，使其参数为问题所要求的解，然后通过对模型的观察或抽样来计算所求参数的统计特征，最后给出所求解的近似值，而解的精确度可用估计值的标准误差来表示［9］。

蒙特卡罗法的采样次数与系统的规模无关，也不需要对实际问题作过多简化和假设，而且考虑的更加全面，所以在进行大规模电力系统的稳定性评估时使用蒙特卡罗法更具有优越性。

1.2 基于蒙特卡罗方法的分析方法

基于蒙特卡罗方法的电力系统稳定性分析，主要包括序贯仿真算法和非序贯仿真算法两种。

序贯仿真算法能够精确地模拟系统处于各状态的持续时间及状态间的转移频率。对受时间、天气等因素影响显著模型，如风力发电、太阳能发电等时变电源，以及峰谷差异较大的时变负荷的电力系统稳定性分析，更能符合实际特性，可提高计算结果的可信度。但是序贯概率抽样算法所获得的系统随机状态序列中，相邻系统状态之间通常仅有少量，甚至仅是一个状态的差别，因此抽样效率低、收敛缓慢、计算费用很高，同时分析大系统时对计算机内存要求极高［10］。

非序贯抽样算法直接对系统元件的随机状态抽样，不考虑状态转移和时序信息，具有模型简单、内存需求低、收敛速度显著优于序贯抽样算法的优点，适合应用于大规模电力系统评估计算以及对计算速度要求较高的场合。本文采用非序贯抽样算法进行电力系统的暂态稳定性评估，其中状态采用方法和采样模型是该方法的关键。

1.3 蒙特卡罗的状态采样

蒙特卡罗仿真过程中，部分不确定参数模型可通过历史数据获得，或者假定为一个概率分布函数。系统状态可以通过对元件的概率特性进行随机抽样来得到，而元件的概率特性则可用一个处于［0，1］之间的均匀分布来描述。假设每个元件只有故障和运行两种状态并且元件故障是彼此独立的事件，令PFk表示元件k的无效度，抽取一个取值区间为［0，1］的均匀分布随机数Uk，则有

抽取m 个随机数（U1，…，Uk，…，Um），运用式（1）则能确定一个系统状态为

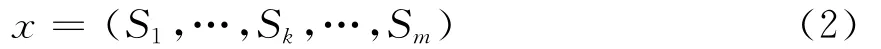
重复上述过程NS次，则能得到一个包含NS个系统状态样本的集合 X ＝ （x1，x2，…，xNS），X 中的样本不具有唯一性，可能存在多个重复的系统状态。

1.4 误差分析与收敛判据

概率论中的大数法则和中心极限定理是蒙特卡罗方法的理论基础［9］。大数法则保证在抽取足够多的样本之后，蒙特卡罗方法取得的估计值收敛于待求量的真值；中心极限定理则为分析蒙特卡罗方法的计算误差提供了理论依据，若F（xi）表示以系统状态xi作为自变量的某稳定性指标测试函数；用（F）表示随机函数的样本均值，其估值可表示为

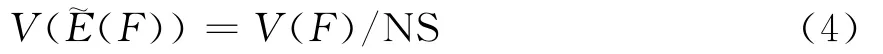
在实际应用中，样本均值E～（F）的不确定性也可以用方差系数β表示，即

2 蒙特卡罗方法在电力系统中的应用

2.1 故障前系统状态的选择

系统网络拓扑和发电机状态的随机抽取可以用状态抽样方法得到。系统负荷随时间而变化，由于负荷的非同时性，以及网络约束和其它因素，某一条线路上的最大负载水平并不一定出现在系统峰荷时段。

在暂态稳定的概率评估中，可以使用多级水平负荷模型的概念，即基于系统负荷的概率分布，给出每一个负荷水平的概率。在评估中应该通过母线负荷间的分配关系，准备每个系统负荷水平下的潮流数据，其中母线负荷分配关系可根据变电站的负荷曲线得到。

2.2 基于蒙特卡罗的概率稳定性故障模型

利用以下5种模型来描述故障事件的不确定性。

1）系统运行方式的概率模型

设系统常见的运行方式有nm种，第i种运行方式发生的概率为Pr（Ai），不考虑其他运行方式，则有

若只关心某种运行方式下系统保持稳定的概率，则有Pr（Ai）＝1（即相当于nm＝1）。

2）故障发生的概率模型

当不考虑天气变化对输电线路可靠性的影响时，线路故障率可用一段时间内线路故障次数表示。由于多条线路同时发生故障的概率忽略不计，线路 上发生故障的概率Pr（Bi）为

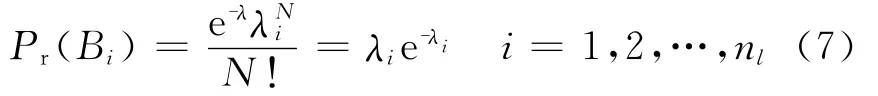
式中：λi为所观察的时间（例如一年）内线路Bi的故障频率；nl为系统中线路总数。故障是否发生的Monte－Carlo抽样描述如图2所示，若抽取的R≤Pr（Bi），则表示故障发生，否则，表示故障不会发生。

图1 抽取故障是否发生的Monte－Carlo描述Fig.1 Description of failure occurred with Monte－Carlo method

3）故障类型的概率模型

不同类型的故障发生的概率与线路电压等级、网络结构以及天气状况有关。对某条特定线路，类型为Ci的故障发生的频率为fi，则其发生概率为

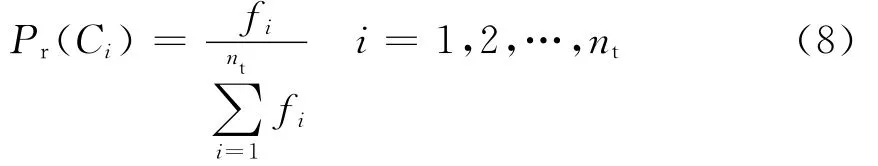
式中：Pr（Ci）表示故障类型Ci发生的概率；nt表示故障类型总数。

对系统暂态稳定性起主要影响的故障通常有4种，三相故障、两相接地故障、两相故障和单相接地故障。按照故障概率模型，涉及故障类型的Monte Carlo模拟抽样描述，若故障的概率可分别用Pr（f（3）），Pr（f（1，1）），Pr（f（2））和Pr（f（1））描述。将4种故障类型的概率值连续置于［0，1］区间，并产生一个在区间均匀分布的随机数R，R的位置表明在抽样中哪个类型被随机地选定，如图2所示。例如当R随机抽样在Pr（f（1））区域内，则表示发生单相故障。

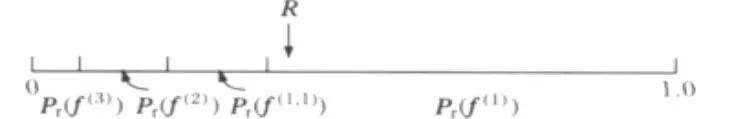
图2 Monte Carlo模拟故障类型抽样描述Fig.2 Description of fault type with Monte Carlo Method

4）故障位置的概率模型

一般而言，输电线路故障点上的信息较少，很难确定天气、地理条件等对线路故障的影响，一般可以认为线路上每一位置发生故障的机会是相同。为了研究问题的方便，有时还需要将线路的故障位置进一步简化。若考虑将线路分成三部分，可分别用首端、中间和末端典型点代替，并假设线路各点发生故障的可能性和它们所代表的长度成正比，则得到图3所示的线路故障位置的离散概率分布，且有

式中，Pr（Di）表示线路上第i个故障点发生故障的概率。

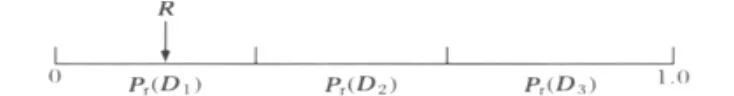
图3 Monte Carlo模拟线路故障发送地点Fig.3 Description of line fault location occurred with Monte Carlo Method

5）故障清除时间的概率模型

故障清除包括故障检测，继电保护和开关动作三部分。一般假定故障检测是瞬时完成的，而继电保护和开关动作需要的时间被假定是随机变量，且服从正态分布。

故障切除时间的概率密度分布可通过保护装置的历史数据经统计分析得出，在缺少数据或数据不足的情况下，可得

式中μ和σ分别为故障清除时间的均值和方差，x为在［－1，1］范围内抽取的一个随机数。

2.3 电力系统概率稳定性指标

电力系统概率暂态稳定性评估的最终目标是获得系统量化的可靠性指标，为电力系统的规划和运行提供数据支持，采用了两个比较主要的稳定性指标，具体如下：

（1）电力系统暂态稳定性失稳概率POTS（probabilistic of transient stability），计算公式如下

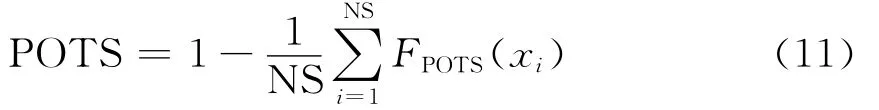
式中：NS为系统随机状态的数目；FPOTS（xi）表示系统在随机状态xi下系统的暂态稳定性分析失稳结果，失稳情况下FPOTS（xi）＝1，稳定情况下FPOTS（xi）＝0。

（2）若考虑到系统的可靠性，也可以用电力不足概率LOLP（loss of load probability）指标，表示系统中出现停电事件的概率，计算公式为

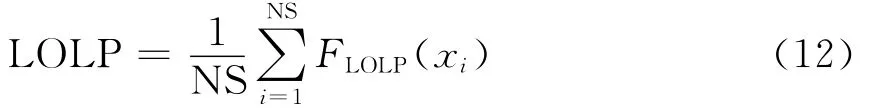
式中，FLOLP为与LOLP对应的试验函数，由系统随机状态向量按下式决定

3 蒙特卡洛方法在电力系统暂态稳定评估流程

基于蒙特卡罗方法的暂态稳定评估流程如图4所示，其中暂态稳定性评估方法及分析效率是该评估流程的关键。

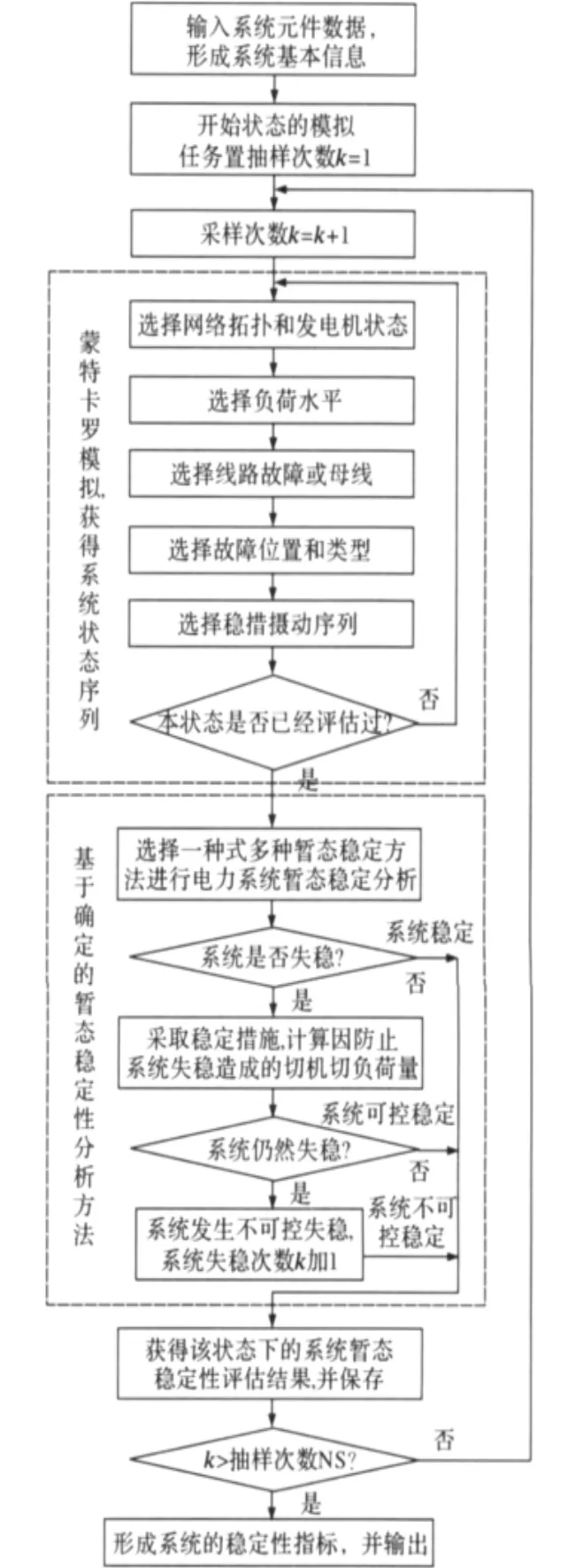
图4 基于蒙特卡罗方法的暂态稳定性评估流程Fig.4 Assessment process of power system transient stability based on Monte Carlo method

目前求解电力系统暂态稳定问题的分析方法大致有三种：时域仿真法、直接法以及将前面二者结合起来的混合算法。混合算法是近20年发展起来的一种比较实用的电力系统暂态稳定性分析方法。它的基本特征是将数值仿真法和直接法相结合，不仅模型适应能力强，而且能够得到反映系统暂态稳定程度的定量指标。因而它一经问世便受到国内外研究人员的普遍重视，而且现已开发应用于实际大型现代电力系统在线稳定性分析中。

在实践过程中，对于Mento Carlo方法获得的抽样故障，可调用BPA等商业分析软件进行暂态稳定仿真，并采用能量函数等方法对该故障进行稳定裕度等分析，具体分析方法可参考文献［12］。

4 算例分析

本文以南方某省级电网2010年夏重负荷典型运行方式为算例进行分析，系统峰值负荷总量为72 000MW。算例系统内110kV级以上节点数为832个，线路总数超过1 200条，线路的故障类型、故障位置以及它们的概率分布采用第2.2节模型，故障类型选择N－1和N－2双回线路故障两种情况。

算例首先分析了计算精度随抽样次数增加的变化规律。由表1可见，在抽样过程中，试验函数的方差基本保持不变，这是因为试验函数的方差取决于试验函数的特性和状态变量的概率分布函数，而与抽样次数无关。随着抽样次数的增加，稳定性指标的估计值趋于稳定，方差系数逐渐减小，计算精度提高。

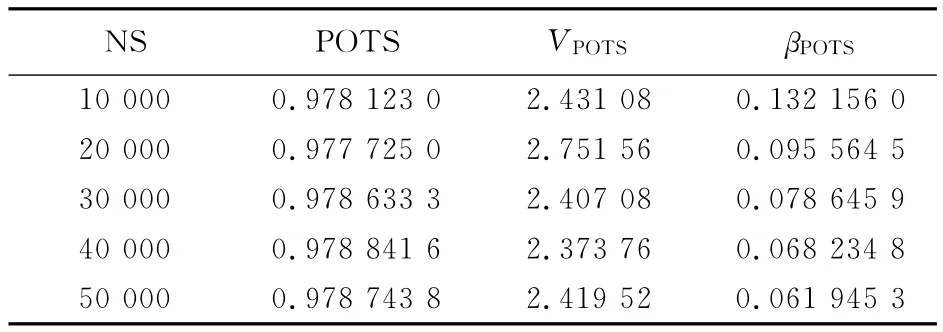
表1 采用Monte Carlo法对POTS的稳定性评估结果Tab.1 Transient Stability index of POTS with Monte Carlo

βPOTS随抽样次数NS的变化规律如图5所示，可以看出，稳定性指标的计算精度随着抽样次数的增加而提高，但提高的速度越来越缓慢，这种现象可以从式（3）～式（5）得到解释。随着抽样次数的增大，方差系数减小的速度越来越慢，造成了计算效率的急剧下降。因此在计算精度要求较高的情况下，依靠增大抽样次数来降低β需要庞大的计算量，且难以满足精度要求。

算例同样分析了负荷水平的增加和继电保护和开关动作时间对于系统稳定性的影响。图6描述了以当前负荷水平为基础，每变化5%时对系统稳定性指标的影响，由图可以看出，随着负荷水平的增加，系统失稳概率呈非线性递增。

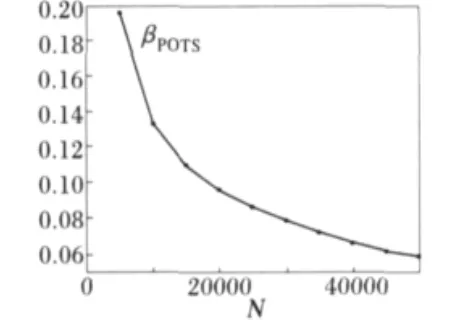
图5 不同抽样次数下的βPOTSFig.5 βPOTSwith different sampling occasions

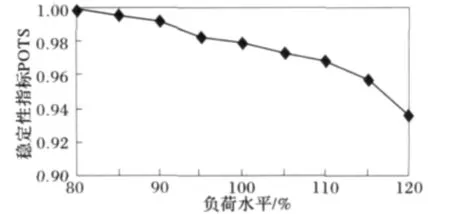
图6 不同抽样次数下的βPOTSFig.6 βPOTSwith different sampling occasions

表2 tcr期望值对系统暂态稳定性的影响Tab.2 Aaffection of tcrexpectations on system transient stability

表2描述了10 000次系统故障抽样情况下继电保护和开关动作需要时间tcr的期望值变化对系统稳定性的影响。故障类型包括所有设备线路的N－1故障，以及N－2双回线路故障，随着期望时间的增加，故障失稳概率呈加速上升趋势，当tcr的期望值由0.09s上升到0.12s时候，不稳定性概率从0.06% 上升到2.45%。

5 结语

电力系统暂态稳定性是可靠性的重要方面，涉及大量不确定性因素，而每次暂态稳定分析却必须针对特定的场景，需要一个两层的不确定性计算框架：其下层用确定性方法分析各指定的场景，用定性方法来判断某特定故障是否会稳定，以及带来损失；上层利用概率的概念来对大量分析场景进行抽样，并综合下层分析的结果，来评估暂态稳定性。因此在进行蒙特卡罗方法的应用时，需要与暂态稳定分析方法紧密结合，才能达到切实模拟系统的运行情况，快速准确获得评估分析结果。

［1］Moulin L S，da Silva A P A，El－Sharkawi M A，et al.Support vector machines for transient stability analysis of large－scale power systems［J］.IEEE Trans on Power Systems，2004，19（2）：818－825.

［2］谢惠藩，王海军，陈潜（Xie Huifan，Wang Haijun，Chen Qian）.云广特高压直流对南方电网稳定性影响（Influence of Yun－Guang UHVDC transmission system on power system stability of CSG）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2010，22（6）：130－137.

［3］Kong Xiangyu，Fang Dazhong，Chung T S.Economy and reliability evaluation of generating including wind energy systems［C］∥Third IEEE International Conference on Electric Unity Deregulation，Nanjing，China：2008.

［4］李文沅，卢继平（Li Wenyuan，Lu Jiping）.暂态稳定概率评估的蒙特卡罗方法（Monte Carlo method for probabilistic transient stability assessment）［J］.中国电机工程学报（Proceedings of the CSEE），2005，25（10）：18－23.

［5］Billinton R，Wangdee W.Predicting bulk electricity system reliability performance indices using sequential Monte Carlo simulation［J］.IEEE Trans on Power Delivery，2006，21（2）：909－917.

［6］程林，郭永基（Cheng Lin，Guo Yongji）.暂态能量函数法用于可靠性安全性评估（Transient energy function algorithm for reliability security evaluation）［J］.清华大学学报：自然科学版（Journal of Tsinghua U－niversity：Science and Technology），2001，41（3）：5－8.

［7］赵渊，徐焜耀，吴彬（Zhao Yuan，Xu Kunyao，Wu Bin）.大电力系统可靠性评估的蒙特卡洛仿真及概率密度估计 （Bulk power system reliability assessment using Monte Carlo simulation and probabilitydensity estimation）［J］.重庆大学学报：自然科学版（Journal of Chongqing University：Natural Science Edition），2007，30（12）：16－20.

［8］赵渊，周家启，刘志宏（Zhao Yuan，Zhou Jiaqi，Liu Zhihong）.大电网可靠性的序贯和非序贯蒙特卡洛仿真的收敛性分析及比较（Convergence analysis and comparison of sequential and nonsequential Monte－Carlo simulation for bulk power system reliability assessment）［J］.电工技术学报（Transactions of China Electrotechnical Society），2009，24（11）：127－133.

［9］Kong Xiangyu，Cui Kai，Jia Hongjie.Capacity credit evaluation of wind power with sequential Monte Carlo method［C］∥International Conference on E－Product E－Service and E－Entertainment， Henan， China：2010.

［10］宋晓通（Song Xiaotong）.基于蒙特卡罗方法的电力系统可靠性评估（Study on Reliability Evaluation of Power System Based on Monte Carlo Simulation）［D］.济南：山东大学电气工程学院 （Jinan：School of Electrical Engineering of Shandong University），2008.

［11］叶圣永，王晓茹，刘志刚，等（Ye Shengyong，Wang Xiaoru，Liu Zhigang，et al）.电力系统暂态稳定概率评估方法（Approach to assess power system transient stability probability）［J］.电网技术（Power System Technology），2009，33（6）：19－23，28.

［12］崔凯，房大中，钟德成（Cui Kai，Fang Dazhong，Chung Takshing）.电力系统暂态稳定性概率评估方法研究（Study on probabilistic assessment method for power system transient stability）［J］.电 网 技 术 （Power System Technology），2005，29（1）：44－49.