基于同步参考坐标系的三相数字锁相环

洪小圆 吕征宇

（浙江大学电力电子国家专业实验室 杭州 310027）

1 引言

锁相环广泛应用于通信[1-3]、电力电子[4-7]和电力传动[7-9]中，在工业应用中起着举足轻重的作用，而基于同步参考坐标系的三相数字锁相环以其实现的简易及对电网畸变的较好抑制能力，在并网逆变器、无功补偿器、整流器等与电网连接的三相系统中得到了越来越多的关注[10-14]。从控制角度出发，锁相环的性能包括稳定性、稳态性能和动态性能[15]，为了提高锁相环的性能，可基于其线性模型或非线性模型对各组成单元的可更改部分进行完善。文献[16-18]通过构造李雅普诺夫函数验证了一系列模拟锁相环、过零数字锁相环及一系列典型数字锁相环非线性模型阶跃输入时的稳定性，为锁相环的设计提供参考，文献[19]比较了李雅普诺夫和拉塞尔不变集理论用于验证锁相环全局稳定性的区别；文献[10-14]针对基于同步参考坐标系的三相锁相环，提出了基于其线性模型的PI参数的优化设计方法，以更好地权衡稳态性能及动态性能。然而并没有文献针对基于同步参考坐标系的三相数字锁相环稳定性进行论证，PI参数之外的影响动态性能的因素也没有得到关注。

本文首先简述了基于同步参考坐标系的三相数字锁相环原理，总结出影响锁相环动态性能的主要因素，通过构造李雅普诺夫函数分析上述因素对锁相环非线性模型的全局渐进稳定性的影响，然后针对 PI参数以外的影响因素提出了采用相序识别以缩短锁相环调整时间的方法，并对其具体实现进行分析，最后给出仿真和实验结果。

2 基于同步参考坐标系的三相锁相环原理

假定三相电网电压幅值、频率恒定，各相之间相位相差120°，如图1所示，三相电网电压合成空间矢量 us以恒定角频率ω0旋转，与β轴负半轴夹角为θ*，θ*随时间斜率上升。虚拟一以角频率ω旋转的dq坐标系，其d轴与β轴负半轴夹角为θ，为已知量。电压矢量us在dq坐标系上投影为usd、usq，usq指示着电压矢量与虚拟坐标系间的相位关系，当 usq＞0时，电压矢量us领先于d轴，当usq=0时，电压矢量us与d轴同相位，当usq＜0，电压矢量us滞后于d轴。因此以usq为反馈，以虚拟坐标系的旋转角频率ω为控制量，以usq=0为控制目标，即可控制d轴跟随us并获得当前电网各相电压的相位，据此建立的锁相环结构框图如图2所示，锁相环通过电压矢量在q轴上的投影进行鉴相，以比例积分环节为环路滤波器。假设三相电网电压的幅值为 Usm，则电压矢量us在q轴上的投影可表示为

图1 三相电压空间矢量图Fig.1 Vector graph of three-phase voltage

图2 基于同步参考坐标系的锁相环结构框图Fig.2 Phase-locked loop structure based on synchronous reference frame

正弦函数是个非线性函数，非线性因素使 PI参数的设计及系统稳态、动态性能的分析变得很困难，为此引入稳态工作点附近的小信号线性近似，当θ*-θ 很小时，sin(θ*-θ)≈θ*-θ，据此可得锁相环的线性模型如图3所示，令θ*=ω0t+θ0，图3中加入了对基准角频率ω0及基准相位θ0的静态偏置补偿，分别为0ω′和0θ′，则可推导锁相环的输出函数为（推导过程见附录）

由上式可知，锁相环的动态性能由 PI参数 kp与ki、角频率静态偏置补偿误差 ω0′ -ω0、相位静态偏置补偿误差 θ0′ -θ0决定。其中PI参数可以根据线性模型开环传递函数的 Bode图设计，为了提高锁相环的响应速度，可增大kp以提高系统的带宽，然而锁相环实际上是非线性系统，在大信号输入情况下上述线性模型与实际偏差大，因此有必要分析基于线性模型设计的PI参数对系统稳定性的影响。

图3 三相数字锁相环线性模型Fig.3 Linear model of three-phase digital PLL

3 基于李雅普诺夫函数的锁相环稳定性研究

图4所示为基于同步参考坐标系的三相数字锁相环的非线性模型，以锁相相位误差 e及角频率ω为状态变量建立锁相环状态方程为

式中，x1指代 e，x2指代ω。令=0，=0 求得锁相环的平衡点为：（kπ，ω0），k=0，±1，±2，…，由于鉴相器是周期为2π的正弦函数，因此实际平衡点只有两个：（0，ω0）和（π，ω0），则锁相相位误差e只需考虑一个周期的范围，即e∈ (-π,π]。

如果能够证明锁相环在其中一个平衡点上全局渐进稳定，那么锁相环在另外一个平衡点必定不会稳定。

图4 三相数字锁相环非线性模型Fig.4 Nonlinear model of three-phase digital PLL

假定锁相环在平衡点（0，ω0）上渐进稳定，构造李雅普诺夫函数

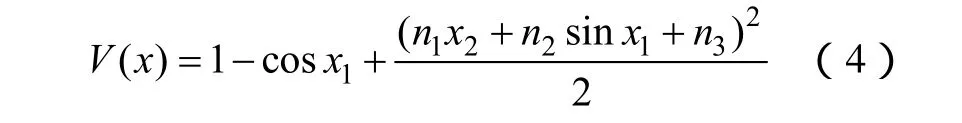
式中， x1∈ (-π, π]，x2∈R，n1、n2、n3为待定系数。

根据李雅普诺夫稳定性定理[20]，锁相环在平衡点（0，ω0）上渐进稳定的充分条件是V(x)满足下列等式及不等式

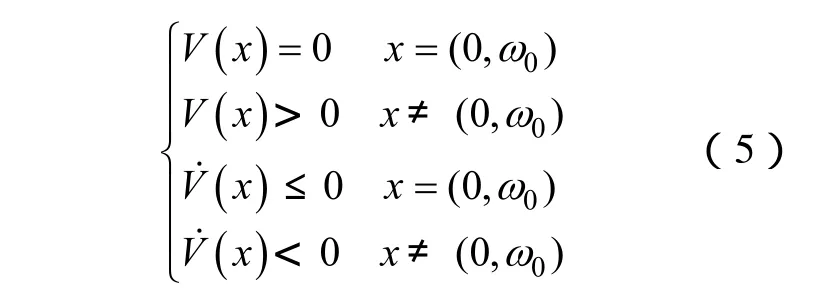
则可推导出系数n1、n2、n3为

由上式可知n1、n2、n3有实数解的前提是kp＞0且ki＞0，也就是说基于同步参考坐标系的三相数字锁相环稳定性只与PI参数有关，而与角频率静态偏置补偿误差和相位静态偏置补偿误差无关。由于锁相环引入比例积分环节构成负反馈闭环系统势必满足此前提条件，因此基于线性模型设计的PI参数不会影响锁相环的稳定性。

4 锁相环动态性能的改善

由式 2可知，减小角频率静态偏置补偿误差ω0′ -ω0及相位静态偏置补偿误差 θ0′ -θ0均能缩短锁相环的调整时间。电网频率允许偏差值为±1Hz[21]，因此只要能识别ω0的正负即可将角频率静态偏置补偿误差控制在 2%范围内。图 5所示为与电网连接的三相功率系统结构框图，电网侧的三相端子用a、b、c表示，功率侧的三相端子用x、y、z表示，三相坐标轴用A、B、C表示，电网侧与功率侧在硬件上用导线相连，而功率侧与三相坐标轴在软件上对应，功率侧的三相电压 ux、uy、uz通过采样输入到DSP，根据其与三相坐标轴的对应关系转换成电压矢量，若电压矢量逆时针旋转，ω0＞0，为正序，若电压矢量顺时针旋转，ω0＜0，为负序，因此识别ω0的正负实际上就是识别三相坐标轴上三个电压量合成电压矢量的相序。

图5 三相功率系统结构框图Fig.5 Three-phase system structure diagram

4.1 相序及相位识别原理

电网侧三相电压可表示为

功率侧三相电压可表示为

式中，m=0、±1，决定各相初始相位，n=±1，决定各相间的相位差，m和n的不同组合对应功率侧与电网侧的不同硬件接法。令 xyz→ABC，单杠箭头表示功率侧三相电压按顺序分别置于三相坐标轴A、B、C上，则可推算出功率侧三相电压合成的电压矢量为

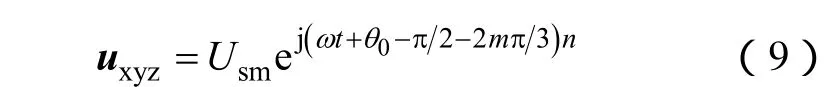
由式9可看出相序只跟n的取值有关，将所有6种接法的相序总结见表1。

表1 各种接法对应的相序Tab.1 Phase sequences of different connections

表1中双杠箭头表示按顺序连接，（如bac⇒xyz表示b与x相连，a与y相连，c与z相连），对比正序与负序的三相电压波形可归纳出如表2所示的规律，只需等待任意一相电压过零，将过零相置于A轴，其余两相任意分配到B轴和C轴即可判断相序。以图6三相正弦波为例，可看出a相电压负向过零时，b相电压为正，c相电压为负，若abc⇒xyz→ ABC ，则对应表 2中正序的第一行；若acb⇒ xyz → ABC ，则对应表2中负序的第一行。

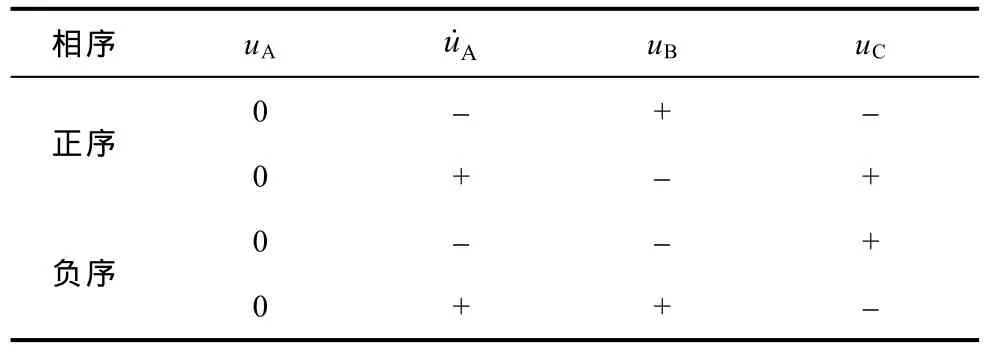
表2 相序判断依据Tab.2 Phase sequence identification rule

上述相序识别方法要求检测过零点及过零点的电压变化趋势，正向（负向）过零相的相位为0(π)，将过零相置于A轴，并判断其他两相电压的正负，按照表2规则，将正（负）电压相置于C轴，将负（正）电压相置于B轴，则在程序内部将电网侧与功率侧的所有硬件接法均连接成正序接法，至此可实现角频率静态偏置补偿和相位静态偏置补偿。

4.2 相序及相位识别的实现及分析

实现上述相序识别方法需要在检测出任意一相过零点时判断其电压的变化趋势以及其他两相电压的正负，考虑到电网电压含有谐波且电压采样时引入干扰，实际采样得到的电压在理想值上下波动，假设波动范围为±Uf，如图 6所示，a相电压采样结果在a+及a-范围内，可能出现多个过零点及ua(θ1)＞ua(θ2)的情况，导致过零点检测及其电压变化趋势的判断变得不可靠。从图6可看出，某相过零时，其他两相距离零电压均有段距离，因此相序识别不需要在精确的过零时刻进行，为此可引入过零点的滞环判断，滞环上下限为±Ut，采样电压小于-Ut判定为负电压，大于Ut判定为正电压，而处于两者之间为模糊状态，不予采用。当判定出某相电压为正（负）时，只需等到该相电压变为负（正），即可判定该相电压负向（正向）过零。而保证电压正负判定正确的前提条件是

滞环上下限幅值越大，则正负判定的抗干扰能力越强，但是过零电压变化趋势的判定时间偏离过零点越长，可能出现其他两相电压已经反向的问题，导致相序的错误识别。以图 6中所示为例，a相正向过零时，c相为正，b相为负，随着θ增加，c相比b相更早向零电压靠近，因此这里只需分析c相反向的问题。

图6 三相电压及其扰动示意图Fig.6 Three-phase voltage and disturbance

a相过零电压变化趋势判定时刻可由下式求出：

式中，ufa为 a相干扰电压，|ufa|≤Uf，而该判定时刻的c相电压为

式中，ufc为c相干扰电压，|ufc|≤Uf，当ufa=ufc=-uf判定时刻的c相电压最小，可表示为

综合抗干扰裕量取决于 Ut-Uf及 ucmin(θa)中较小值，Ut-Uf随 Ut增加而增加，而 ucmin(θa)随 Ut增加而减小，为了获得最大的综合抗干扰裕量，令Ut-Uf=ucmin(θa)，得

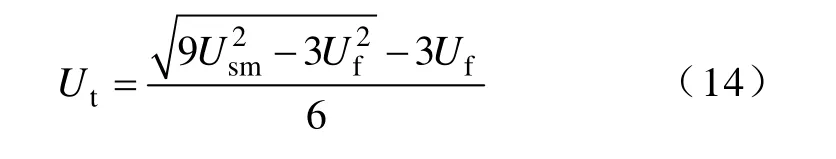
不同相过零及不同电压变化趋势过零的分析与上述相似，Ut的推导结果相同，此处不予赘述。根据国标[22]规定，0.38kV公用电网电压总谐波畸变率限值为5%，即 Uf=0.05Usm，则综合抗干扰裕量最大的滞环宽度应该取Ut=0.475Usm。

但是滞环电压 Ut越大则过零点相位的计算误差越大，为了减小相位静态偏置补偿误差导致的锁相环调整时间，可以在保证式（10）成立的前提下尽量减小Ut。

5 仿真及实验结果

5.1 角频率静态偏置补偿

图7 三相数字锁相环simulink仿真模型Fig.7 Simulink model of three-phase digital PLL

图8 不同角频率静态偏置补偿时的相位跟踪误差Fig.8 Track error of phase with different compensation of angular frequency static bias

5.2 相位静态偏置补偿

分别对未加入和加入相位静态偏置补偿的锁相环进行实验比较，实验涵盖2π弧度范围内三相电压的6个过零点，即初始相位θ0为0、π/3、2π/3、π、4π/3和5π/3，过零点采用文中所述滞环判断，滞环电压幅值为30V。两组锁相环实验均加入了角频率静态偏置补偿，为 ω0′=100π，相序已经识别并在软件中校正为正序。图9、图10中红色波形为电网线电压波形，由电压霍尔采样经 A-D转换到 DSP内部再换算后经D-A模块输出所得，蓝色波形为锁相环输出相位的正弦值，由 DSP内部计算后经 D-A模块输出所得。波形中左边线起 20ms内的波形为程序内部的初始化，没有实际的物理意义。

图9所示为未加入相位静态偏置补偿的锁相环实验波形，即θ0′=0，锁相环调整时间最短的是θ0=0情况，如图 9a；其次是相差π/3情况，分别是电网电压领先和滞后锁相初始输出π/3的情况，如图 9b和图9f；再次是相差2π/3情况，如图9c和图9e；最后是相差π的情况，调整时间最长，如图 9d，验证了锁相环的调整时间与相位静态偏置补偿误差大小有关。

图9 未加入相位静态偏置补偿的锁相环实验波形Fig.9 Experimental waveforms of phase-locked loop without initial phase compensation

图10所示为加入相位静态偏置补偿的锁相环实验波形，即 θ0′ ≈θ0，无论功率侧与电网侧相连时的电网相位如何，最长只需等待1/6电网基波周期，在过零点出现后即可识别当前电网相位并开始锁相，可以看出六种初始相位的锁相环调整时间相近，此时间取决于过零判断的滞环范围。

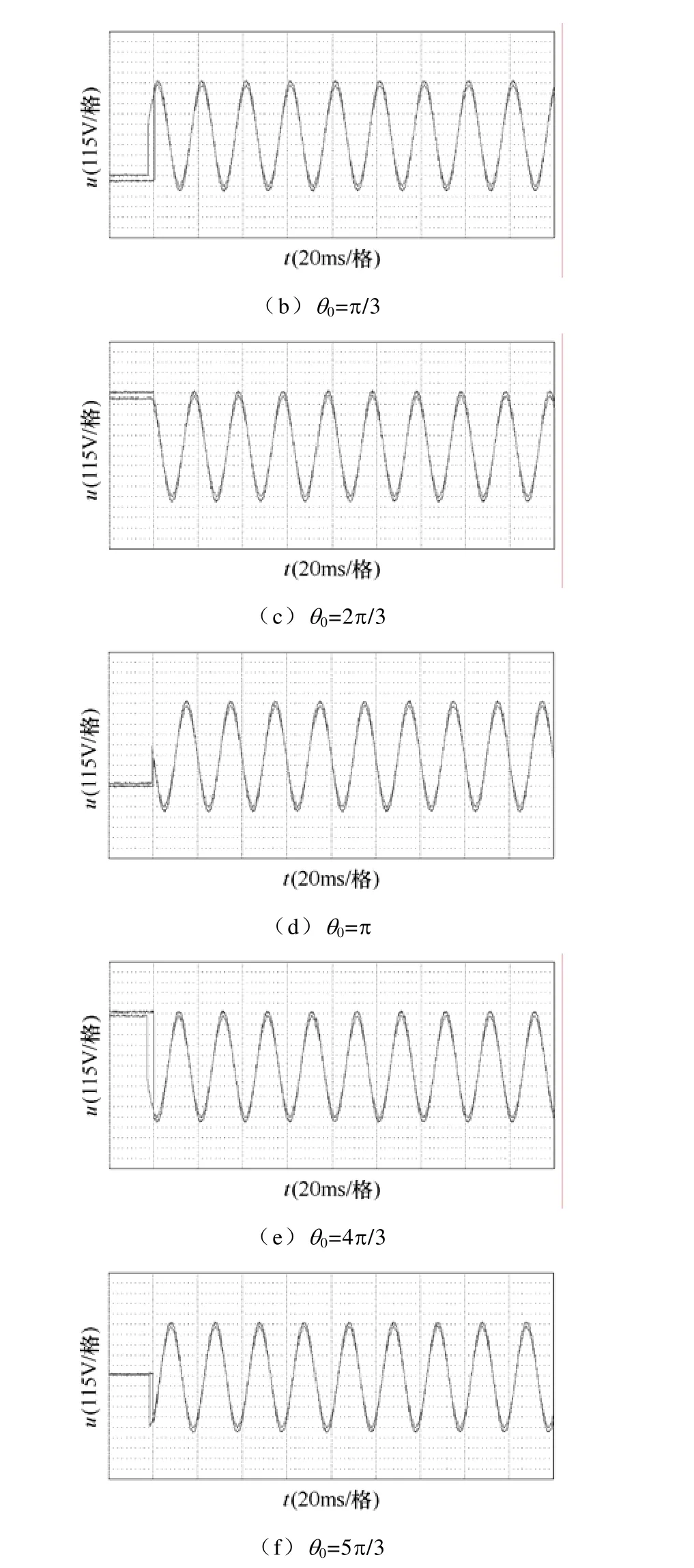
图10 加入相位静态偏置补偿的锁相环实验波形Fig.10 Experimental waveforms of phase-locked loop with initial phase compensation

6 结论

本文在简述基于同步参考坐标系的三相数字锁相环原理后，得出了决定锁相环调整时间的三个因素包括PI参数的设计、角频率和相位静态偏置补偿误差，通过构造李雅普诺夫函数证明了只要PI参数都大于零，基于非线性模型的锁相环就能稳定，确保了基于线性模型设计的PI参数的合理性，并提出了相序识别方法以给定正确的角频率静态偏置补偿，相序识别的同时实现了相位的近似识别，将识别后的相位用于锁相环的相位静态偏置补偿，在稳定的前提下大大缩短了锁相环的调整时间，仿真和实验结果证明了上述方法的可行性。

附 录

式（2）的推导过程如下。

根据图3可以写出如下等式：

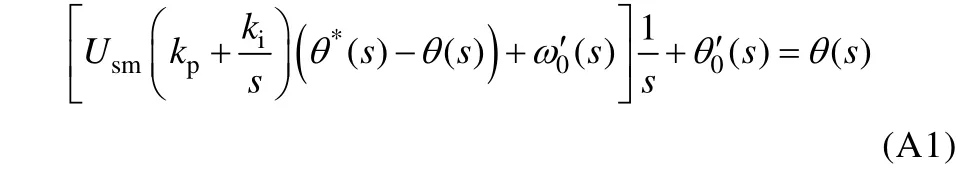
整理与θ (s)相关项置于等式右边，得

[1]Guan Chyun Hsieh, Hung James C.Phase-locked loop techniques-a survey[J].IEEE Transactions on Industrial Electronics, 1996, 43(6): 609-615.

[2]Daniel Abramovitch.Phase-locked loops: a control centric tutorial [C].Proceedings of the American Control Conference, Anchorage, AK USA, 2002.

[3]李亚斌, 彭咏龙, 李和明.自采样比例积分控制全数字锁相环的性能分析和实现[J].中国电机工程学报, 2005, 25(18): 64-69.Li Yabin, Peng Yonglong, Li Heming.The implementation and analysis of a self-sampling PI control all digital phase-locked loop[J].Proceedings of the CSEE, 2005, 25(18): 64-69.

[4]孔雪娟, 罗昉, 康勇.基于周期控制的逆变器全数字锁相环的实现和参数设计[J].中国电机工程学报,2007, 27(1): 60-64.Kong Xuejuan, Luo Fang, Kang Yong.Implement and parameter design of DPLL for invertors based on cycle control[J].Proceedings of the CSEE, 2007,27(1): 60-64.

[5]杨勇, 阮毅, 叶斌英.基于锁相环和虚拟电网磁链的三相并网逆变器[J].电工技术学报, 2010, 25(4):109-114.Yang Yong, Ruan Yi, Ye Binying.Three-phase grid-connected inverters based on PLL and virtual grid flux [J].Transactions of China Electrotechnical Society, 2010, 25(4): 109-114.

[6]龚锦霞, 解大, 张延迟.三相数字锁相环的原理及性能[J].电工技术学报, 2009, 24(10): 94-99, 121.Gong Jinxia, Xie Da, Zhang Yanchi.Principle and performance of the three-phase digital phase-locked loop[J].Transactions of China Electrotechnical Society, 2009, 24(10): 94-99, 121.

[7]庞浩, 俎云霄, 王赞基.一种新型的全数字锁相环[J].中国电机工程学报, 2003, 23(2): 37-41, 131.Pang Hao, Zu Yunxiao, Wang Zanji.A new design of all digital phase-locked loop[J].Proceedings of the CSEE, 2003, 23(2): 37-41, 131.

[8]高金文, 温旭辉, 陈静薇.新型锁相环定子磁链观测器[J].中国电机工程学报, 2007, 27(18): 41-47.Gao Jinwen, Wen Xuhui, Chen Jingwei.Novel motor stator flux observer based on PLL[J].Proceedings of the CSEE, 2007, 27(18): 41-47.

[9]冯志华, 刘强, 刘永斌.基于锁相环的变频器同步跟踪实验[J].电工技术学报, 2006, 21(11): 96-100.Feng Zhihua, Liu Qiang, Liu Yongbin.Experimental study on synchronized tracing control of variable frequency devices based on phase locked loop[J].Transactions of China Electrotechnical Society, 2006,21(11): 96-100.

[10]Timbus A, Teodorescu R, Blaabjerg F, et al.Synchronous methods for three phase distributed power generation systems, an overview and evaluation[C].Proceedings of the Power Electronics Specialists Conference, Recife, Brazil, 2005.

[11]Vikram Kaura, Vladimir Blasko.Operation of a phase locked loop system under distorted utility conditions[J].IEEE Transactions on Industry Applications, 1997, 33(1): 58-63.

[12]Amuda L N, Cardoso Filho B J, Silva S M, et al.Wide bandwidth single and three-phase PLL structures for grid-tied PV systems[C].Proceedings of the Photovoltaic Specialists Conference, Anchorage, AK USA, 2000.

[13]Chung Se Kyo.A phase tracking system for three phase utility interface inverters[J].IEEE Transactions on Power Electronics, 2000, 15(3): 431-438.

[14]Chung Se Kyo.Phase-locked loop for grid-connected three-phase power conversion systems[J].IEE Proceedings on Electric Power Applications, 2000,147(3): 213-219.

[15]Katsuhiko Ogata.Modern control engineering[M].5版.北京: 电子工业出版社, 2007.

[16]Yabramovitch Daniel.Lyapunov redesign of analog phase-lock loops[J].IEEE Transactions on Communications, 1990, 38(12): 2197-2202.

[17]Dan Simon, ElSherief Hossny.Lyapunov stability analyses of digital phase-locked loops[C].Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, San Antonio, TX USA, 1994.

[18]Daniel Abramovitch.Lyapunov redesign of classical digital phase-lock loops[C].Proceedings of the American Control Conference, Denver, Colorado,USA, 2003.

[19]Anders Rantzer.Almost global stability of phase-locked loops[C].Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, Florida USA, 2001.

[20]Khalil Hassan K.Nonlinear systems [M].3版.北京:电子工业出版社, 2007.

[21]林海雪.电压电流频率和电能质量国家标准应用手册[M].北京: 中国电力出版社, 2001.

[22]中国国家标准化管理委员会.GB/T 14549—1993电能质量 公用电网间谐波[S].北京: 中国标准出版社, 1993.