基于角速率和速度增量的捷联惯性导航算法研究

王伟鹏 杨 博 李 方

1．北京航空航天大学宇航学院，北京 1001912.空军工程大学工程学院，西安 710038



基于角速率和速度增量的捷联惯性导航算法研究

王伟鹏1杨 博1李 方2

1．北京航空航天大学宇航学院，北京 1001912.空军工程大学工程学院，西安 710038

捷联惯性导航算法一般是基于惯性器件输出为角速率、比力或角增量、速度增量进行设计的，不能直接应用于陀螺输出为角速率、加速度计输出为速度增量的捷联惯性导航系统。为了解决此问题和满足精度要求，重新设计了一套捷联惯性导航算法：姿态更新算法采用了经典的四阶龙格-库塔法，推导出了一种新的速度更新算法，该算法可以有效补偿速度计算中的划桨效应误差。仿真结果表明，该种速度更新算法仿真速度快、精度高，具有一定的工程实用价值。

角速率；速度增量；四阶龙格-库塔法；划桨效应

捷联惯性导航系统(Strap-down Inertial Navigation System，简称SINS)广泛应用在飞机、舰船、坦克、导弹等海、陆、空、天惯性导航与制导领域。为了提高系统的精度，满足各种载体的导航与制导要求，出现了很多捷联算法研究[1-6]。

由于陀螺仪输出有角速率和角增量两种方式，如微机械陀螺输出为角速率或角增量方式、激光陀螺输出为角增量方式、光纤陀螺输出为角速率方式等；加速度计输出有比力和速度增量两种方式。因此，SINS的解算有以下组合方式[7]： 1)角速率和比力； 2)角增量和速度增量； 3)角增量和比力； 4)角速率和速度增量。在实际惯性导航系统中，因工作环境、技术指标及成本等方面的限制，需要选择不同等级的惯性器件，使得常规的角速率与比力、角增量与速度增量输出方式为主的SINS导航算法不能满足实际系统的设计需求。因此，有必要研究其它不同输出方式的SINS算法，以适应惯性器件多元化的发展[7]。对于惯性器件输出为角速率和速度增量组合方式的SINS算法，目前尚未有文献对其报道，若通过角速率提取角增量后再利用基于增量信号SINS算法解算会带来较大误差。本文针对这种组合方式的SINS算法进行了速度补偿算法方面的研究，鉴于角速率信号能直接连续得到，本文从算法精度和计算量方面综合考虑，选用四阶龙格-库塔法[8]进行姿态更新，详细推导出了一种新型速度更新算法，该算法可以补偿速度解算中的划桨效应[9]，并进行了仿真验证，为后续工程化实现提供了一定的理论依据。

1 新型SINS算法

设i为惯性坐标系，e为地球固联坐标系，n为导航坐标系(文中取东北天地理坐标系)，b为载体坐标系，T为系统采样周期。

1.1 姿态更新

通常姿态更新算法有龙格-库塔法(Range-Kutta)和旋转矢量法[5]。龙格-库塔法直接利用角速率计算载体的姿态四元数；旋转矢量法先利用角增量计算旋转矢量, 再通过旋转矢量计算载体的姿态四元数。因此，对陀螺仪以角速率方式输出的指北方位捷联惯导系统，姿态更新算法采用龙格-库塔法计算载体的姿态四元数较为合理。

设q为四元数，则四元数微分方程为[7]

(1)

(2)

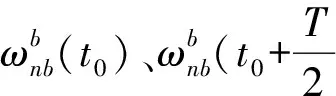
1.2 速度更新和补偿

取地理坐标系为导航坐标系，速度方程[9-10]为

(3)

在[tk,tk+1]对上式进行积分，得tk+1时刻载体在导航坐标系内的速度为

(4)

(5)

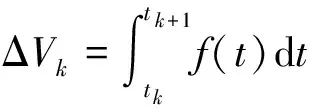
(6)

式中，Δθ(t)为角增量，ΔV(t)为速度增量，ΔVrotk为速度的旋转效应补偿项，该项由运动载体的线运动方向在空间旋转引起；ΔVsculk为速度的划桨效应补偿项，该项由运动载体沿纵轴作线振动和沿横轴作同频同相的角振动引起。对于以角速率和速度增量的方式为输入的捷联惯导系统，速度计算时必须考虑旋转效应和划桨效应补偿项，则不能直接应用式(6)，需重新推导速度的划桨效应补偿项。

(7)

其中，拟合系数分别为a，b，c，A，B，C。

在t∈[tk,tk+1]内，对(7)式积分则

(8)

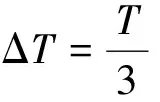
(9)

在ΔT，2ΔT和3ΔT3个时间段内，速度增量的三子样采样值分别为

=AΔT+3BΔT2+7CΔT3

=AΔT+5BΔT2+19CΔT3

(10)

联立式(9)和(10)，求解得拟合系数

(11)

将式(7)和(8)分别代入(6)式计算得

(12)

(13)

式中ωk(1)、ωk(2)和ωk(3)分别为tk+ΔT、tk+2ΔT和tk+13时刻的角速率采样值；Vk(1)、Vk(2)和Vk(3)分别为[tk,tk+1]内速度增量的3个等间隔采样值。

2 仿真验证

整个系统仿真分为两步进行，首先设计轨迹发生器[11]模拟出一条载体的航迹，除了输出载体的姿态、速度和位置等导航参数，还要输出陀螺仪和加速度计的采样值，作为SINS系统解算的输入值。然后以陀螺的角速率、加速度计的速度增量作为仿真输入，将系统仿真的结果和模拟出的载体航迹相比较，检验算法的正确性和补偿效果。

假设载体初始位置为北纬34°14.763′，东经108°54.579′，高度380m，初始速度为0，初始俯仰角为90°，航向角、横滚角为随机角度。在1500s的仿真时间内，前126s为上升阶段，第126s～129s为退出爬升、改平阶段，第129s～900s为匀速直线平飞阶段(巡航段)，巡航段飞行速度(沿纵向)为4.0Ma。

姿态误差、速度误差仿真结果分别如图1和图2所示。从仿真结果中可以看出，在导航飞行全过程中由于算法导致的姿态误差在0.001角分量级，速度误差在0.01m/s量级。

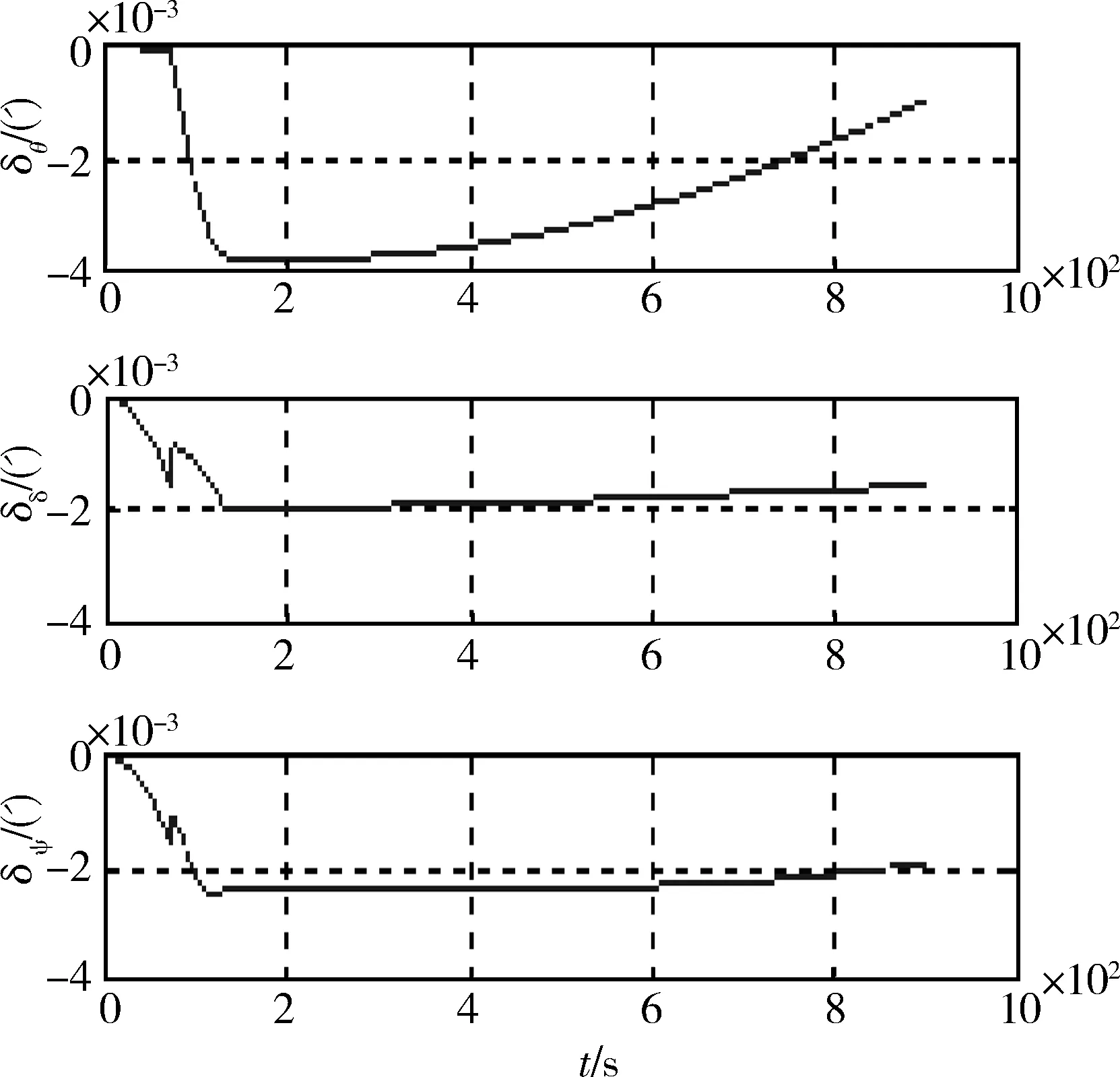
图1 姿态误差

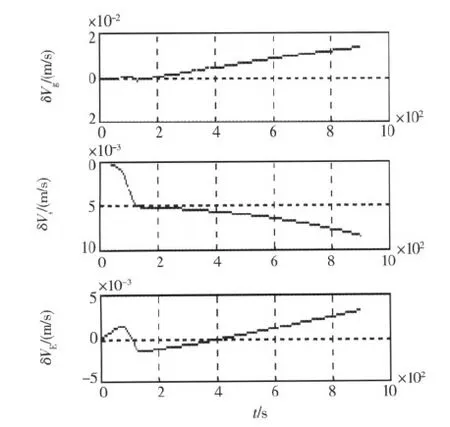
图2 速度误差

3 结论

本文提出了一种惯性器件输出以角速率和速度增量为组合方式的SINS算法，采用经典的四阶龙格-库塔法进行姿态更新，并推导出了一种新的速度更新算法，有效补偿速度计算中的划桨效应误差项。完成了对捷联惯导系统的数字全仿真，从轨迹发生器、捷联解算等方面很好的模拟了捷联惯导系统的工作过程。

仿真结果表明, 文中采用的导航算法可行，具有较好的精度，满足实际系统的要求。

[1] Brotz J E.A New Mathematical Formulation for Strapdown Inertial Navigation [J].IEEE Trans.on Aerospace and Electronic System, 1971,7(1):61-66.

[2] Paul G.Savage.Strapdown Inertial Navigation Integration Algorithm Design part1: Attitude Algorithms[J].Journal of Guidance, Control, and Dynamics,1998,21(1):19-28.

[3] Paul G.Savage.Strapdown Inertial Navigation Integration Algorithm Design part2: Velocity and Position Algorithms[J].Journal of Guidance, Control, and Dynamics,1998,21(2):208-229.

[4] Paul G.Savage.A Unified Mathematical Framework for Strapdown Algorithm Design [J].Journal of Guidance, Control, and Dynamics,2006,29(2):237-249.

[5] 刘危，解旭辉，李圣怡.捷联惯导系统的圆锥误差补偿算法研究[J].南京航空航天大学学报，2004，36(3)：348-352.(LIU Wei,XIE Xu-hui,LI Sheng-yi.Coning Algorithm for Strap-Down Inertial Navigation System[J].Journal of Nanjing University of Aeronautics & Astronautics,2004,36(3):348-352.)

[6] 耿延睿，王养柱，崔中兴.捷联惯导系统划船效应补偿算法研究[J].北京航空航天大学学报，2001，27(6)：694-697.(GENG Yan-rui,WANG Yang-zhu,CUI Zhong-xing.Optimal Design for Sculling algorithms of SINS[J].Journal of Beijing University of Aeronautics and Astronautics,2001,27(6):694-697.)

[7] 秦永元.国际惯性器件发展现状和趋势[J].航空制造技术，2008，(9)：68-69.(QIN Yong-yuan.Current Status and Development Trend of International Inertial Instrument[J].Aeronautical Manufacturing Technology,2008,(9):68-69.)

[8] 王蕴会，赵忠.捷联惯导算法设计和仿真[D].西安：西北工业大学， 2009.

[9] 陈哲.捷联惯导系统原理[M].北京：宇航出版社，1986.

[10] 秦永元.惯性导航[M].北京：科学出版社，2006.

[11] 张 磊，汪 渤.高精度游移方位捷联惯导系统的数字仿真[J].微计算机信息(测控自动化)，2008，22:238-239.(ZHANG Lei,WANG Bo.Digital Simulation of Highly Accurate Free-Orientation SINS[J].Control& Automation,2008,22:238-239.)

[12] 张宗麟.惯性导航与组合导航[M].北京：航空工业出版社，2000.

[13] 颜庆津.数值分析(第三版)[M].北京：北京航空航天大学出版社，2006.

The New Algorithm for Strap-down Inertial Navigation System

WANG Weipeng1YANG Bo1LI Fang2

1.School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China2.Engineering College,Air Force Engineering University,Xi’an 710038,China

Theangularrate,specificforceorangularincrementandvelocityincrementareoftenusedinthealgorithmsofstrap-downinertialsystem.Thealgorithmcannotbeappliedtostrap-downinertialsystemwhoseoutputsignalsareangularrateandvelocityincrement.Inordertosolvetheproblemandmeetprecisionrequirements,asetofnewnavigationalgorithmsaredeveloped.Thefour-orderRange-Kuttamethodisadoptedinattitudeupdate.Anewvelocityupdatealgorithmisdeducedwhichcancompensatescullingeffect.Theobtainedsimulationresultsshowtheeffectivenessofthisapproach.

Angularvelocity;Velocityincrement;Four-orderRange-Kuttamethod;Scullingeffect

2011-12-01

王伟鹏(1982-)，男，山西汾阳人，硕士研究生，主要研究方向为导航制导与控制；杨 博(1963-)，女，北京人，副教授，主要研究方向为导航制导与控制；李 方(1982-)，男，西安人，讲师，主要研究方向为武器系统和制导控制。

V324.2+3

A

1006-3242(2012)03-0003-04