基于输入受限的轨控期间挠性卫星容错控制研究*

傅艳萍 程月华,2 姜 斌

1．南京航空航天大学自动化学院，南京 2100162.南京航空航天大学高新院小卫星工程技术研究中心，南京 210016



基于输入受限的轨控期间挠性卫星容错控制研究*

傅艳萍1程月华1,2姜 斌1

1．南京航空航天大学自动化学院，南京 2100162.南京航空航天大学高新院小卫星工程技术研究中心，南京 210016

轨控期间的卫星由于推力器安装偏差，实施推力时会产生较大的干扰力矩，直接影响到卫星姿态稳定。除此，考虑到执行机构提供的力矩是有限的，为保证系统的稳定性，需在设计控制器的过程中考虑输入受限问题。本文针对卫星执行机构故障情况，综合考虑输入受限和干扰问题，提出一种基于输入受限的挠性卫星姿态容错控制策略，并开展了仿真试验，验证了本文设计的姿态容错控制器的有效性。

挠性卫星；变结构； 容错控制； 输入受限；飞轮故障

卫星由于长时间运行于真空、失重、高低温和强辐射的环境中，执行机构不可避免会发生故障，造成控制系统性能降低，导致系统不稳定，为保证卫星在执行机构故障情况下能够稳定可靠运行，需要设计具备容错能力的卫星姿态控制系统。针对卫星姿态控制系统开展的容错控制，目前取得了较大的进展和丰富的研究成果[1-10]。文献[1]利用LMI的思想，设计刚性卫星含不确定项情况下的容错控制。文献[2]利用动态逆和时延理论,针对4个飞轮为执行机构的卫星开展被动容错控制研究,Cai在文献[3]中提出自适应容错控制器，保证卫星在推力器失效情况下的稳定性。除此，利用滑模[4-5]、观测器方法[6-8]、鲁棒控制[9]等在容错控制中也取得一些研究成果。Ye Jiang 等人则针对挠性卫星的容错控制问题在文献[10]中提出反步自适应方法，考虑挠性卫星在干扰未知、转动惯量未知情况下的挠性卫星被动容错控制，实现故障情况下的容错能力和抑制振动模态。

对于轨控期间的挠性卫星，由于卫星轨道调整期间的轨控推力会激起太阳帆板振动并引起常值变形，从而影响卫星姿态[11]。除此若卫星轨控推力器出现安装偏差，会产生较大的干扰力矩，从而直接影响到卫星姿态[12]。在进行轨控期间挠性卫星的容错控制设计时，若不考虑轨控推力的影响，故障诊断机制会将干扰力矩误判为故障，从而引起不必要的执行机构切换等容错处理措施。文献[13]采用了自适应反步变结构控制方法设计容错控制律实现挠性卫星在轨控期间姿态的稳定。但设计的容错控制器未考虑执行机构的受限问题。而在实际的卫星控制系统中，由于执行机构物理特性的限制和能量消耗的限制，存在执行器的饱和问题，即输入受限。若不考虑输入受限问题，饱和非线性的存在会降低闭环系统的控制性能，甚至导致系统不稳定，造成控制失效。因此，研究输入受限情况下的卫星控制系统的稳定性和鲁棒性对保证系统的稳定性尤为重要[14-17]。

本文针对轨控期间的挠性卫星姿态控制系统，提出输入受限情况下的变结构容错控制方法，在容错控制律中引入饱和约束和自适应律进行控制率调整，实现卫星在故障情况下姿态收敛，同时保证挠性模态的衰减。设计的容错控制律满足饱和约束条件，结构简单，且不需要对故障进行在线辨识，最后通过仿真验证本文提出的方法的有效性。

1 轨控期间的挠性卫星模型

考虑带有单翼大型太阳帆板并配置4个反作用飞轮的轨控期间挠性卫星姿态动力学方程[13]：

(1)

考虑动量轮发生失效故障，将动力学方程(1)改写成

(2)

其中E=diag{e1,e2,e3,e4}为对角矩阵，ei表示第i个动量轮的有效因子，满足0≤ei≤1。当ei=0时第i个动量轮完全失效，ei=1时表示第i个动量轮正常。

采用姿态四元数来描述卫星的运动学模型，表示为

(3)

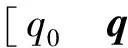
首先对系统方程作一定的处理，引入辅助变量ψ，并定义为

(4)

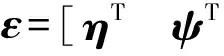
(5)

因此方程(1)可以改写成

(6)

进一步改写成

(7)

其中

将式(7)中的Td视为系统总的干扰项，其中

(8)

2 输入受限情况下的变结构容错控制器设计

2.1 假设条件

为便于控制器的设计，首先给出以下假设条件：

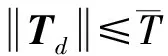
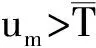
注1：考虑卫星即使是在变轨过程中产生较大的干扰力矩，但也是有界的，所以干扰力矩d有界。除此，在卫星动量轮故障的情况下，ω，V0也存在上界，所以总干扰项Td有界，条件1得到满足。

输入受限情况下卫星姿态控制系统的容错控制问题可以描述为：在考虑干扰和执行机构饱和约束的情况下设计容错控制器保证轨控期间卫星对执行机构故障具有容错能力，并抑制挠性附件的振动，实现limt→∞ω=0,limt→∞q=0。

2.2 变结构容错控制器的设计

在本节中，引入变结构的控制思想进行容错控制器的设计，首先定义滑模面为

(9)

其中，定义k(t)为大于0时的变量，将在下一节中给出k(t)的求解。

考虑输入受限情况，设计容错控制器为式(10)所示

(10)

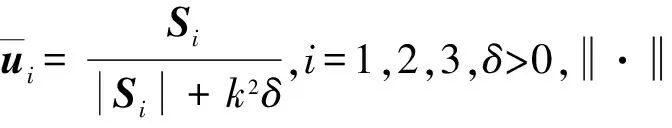
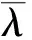
(11)

其中λmax为(LELT)的最大特征值，则所设计的容错控制律能保证闭环系统是全局渐近稳定的。

2.3 稳定性分析

选取李雅普诺夫函数为

(12)

其中P=PT>0，存在正定矩阵QT=Q，满足

(13)

对李雅普诺夫函数求导，可得到

(14)

其中

如果同时选取正定矩阵P和Q，使得

(15)

其中

并考虑控制律式(10)，因此有

(16)

由于

所以由(16)式得到

(17)

利用式(11)

(18)

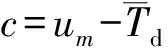
(19)

注2：从控制器的参数设计中看出，矩阵LELT为正定矩阵，若LELT矩阵有一个特征值是0，则意味着卫星姿态有一轴是不可控的，此时控制转换为欠驱动控制问题,不能采用本文提出的方法进行容错控制设计。结合本文的飞轮冗余配置来看，表明最多只能有一个飞轮完全失效。本文设计的容错控制器不需要进行故障信息的在线学习，虽然在稳定性的证明过程中引入了故障参数，但并没有包含在容错控制律中，所以并不需要了解故障的大小。

2.4 稳定控制参数k(t)的分析

(20)

即

对(19)式两边进行积分，得到

(21)

由式(21)可以看出，若存在参数γ满足式(22)

(22)

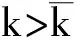
所以当limt→∞k2q(t)=0时，有limt→∞q(t)=0。

注3:尽管在控制律设计中通过选取适当的参数可以有效抑制挠性附件结构的振动，但由于变轨过程中轨控推力的影响，挠性附件会产生常值变形。因此为了更好地抑制挠性结构的振动和常值变形，利用文献[13]的方法设计应变反馈速率补偿器进行振动模态的抑制，本文在此不给出具体的设计过程。

3 仿真分析

本节针对轨控期间挠性卫星姿态控制系统，利用本文提出的变结构自适应容错控制器开展数值仿真。参考文献[13]的挠性卫星参数，考虑航天器整星质量mt=600kg，转动惯量矩阵值取为：

飞轮的初始转速为 0rad/s,转动惯量矩阵值取为：Iw=0.038I4×4kg·m2,4个飞轮的安装分配阵为

帆板相对本体转角为90°,前3阶固有频率分别取0.7681rad/s、1.1038rad/s和1.8733rad/s，阻尼系数分别为ε1=0.005607、ε2=0.008620和ε3=0.01283,平动与挠性振动耦合系数和姿态与挠性振动耦合系数分别为

假设三轴同时从0s开始实施10N常值轨道推力，持续600s，为分析轨控推力偏差对姿态造成的影响，考虑卫星在安装推力器时，由于X轴推力器安装位置偏差，在Z方向上造成-0.025m的位置偏差，在施加10N轨控推力的情况下，则会在Y轴产生0.25N·m的干扰力矩，若不进行姿态控制，轨控推力及推力器偏心安装引起的干扰对卫星振动模态及姿态的影响如图1所示。

图1 轨控推力对卫星姿态的影响

从图1可以看出，轨控推力及由于推力器安装偏心造成的干扰力矩会直接影响卫星的姿态，所以在设计控制器时为保证姿态稳定，必须考虑轨控对姿态的影响。

对于本模型中的飞轮，假设能提供的最大力矩为5N·m，仿真中设定的姿态初值为

q(0)=[0.173648,-0.263201,0.789603,-0.526402]T

考虑4个飞轮中第1个飞轮与第2个飞轮发生部分失效故障，而第3个飞轮则在t=40s时卡死。

根据本文提出的容错控制方法，选择参数为

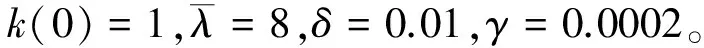
相应的姿态角速度和四元数响应仿真曲线如图2和图3所示，图4与图5分别给出振动模态及飞轮输出力矩的响应曲线。将本文所提出的方法与传统的PD控制进行比较，其中ASMC表示本文的容错控制方法。

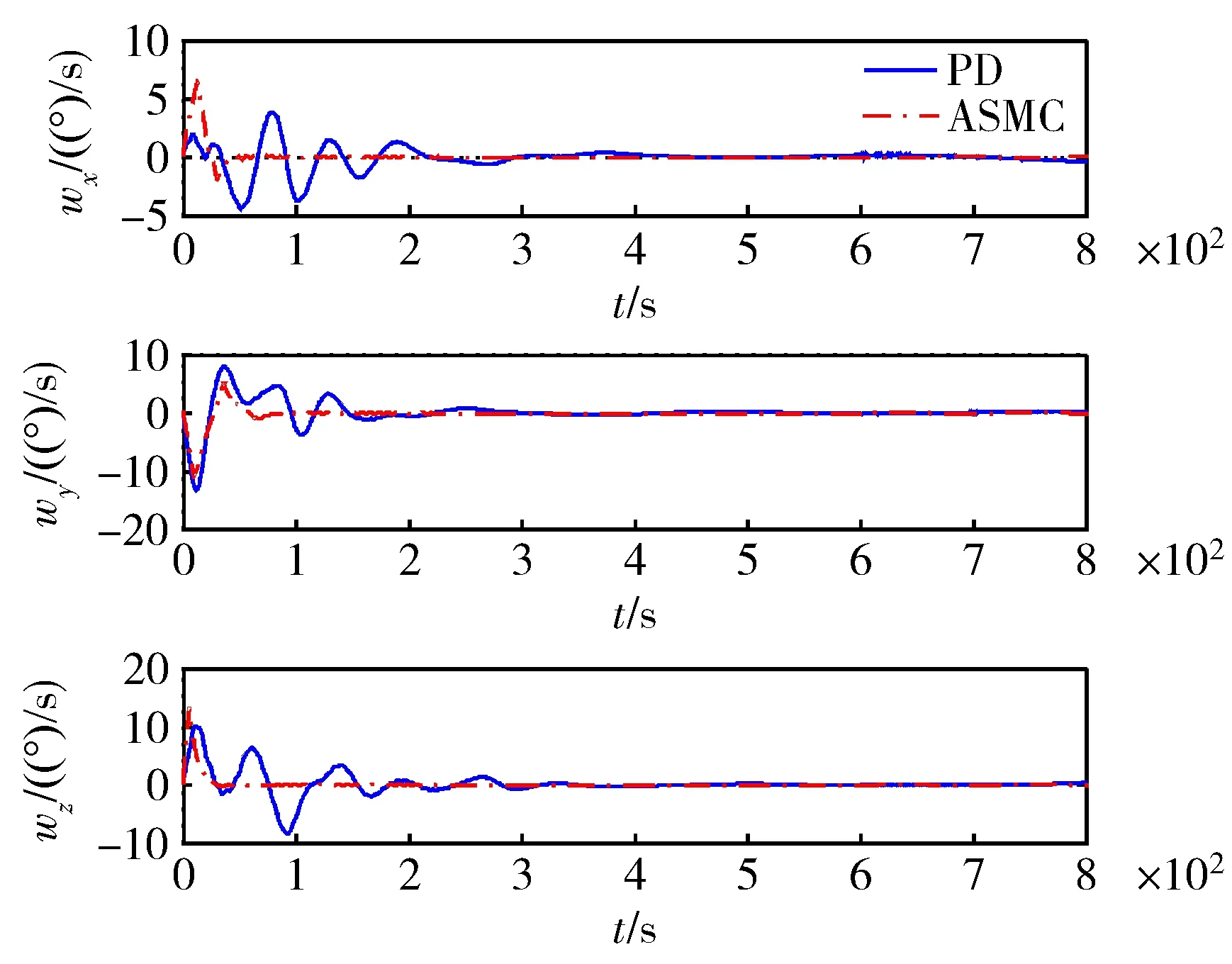
图2 故障情况下角速度响应曲线

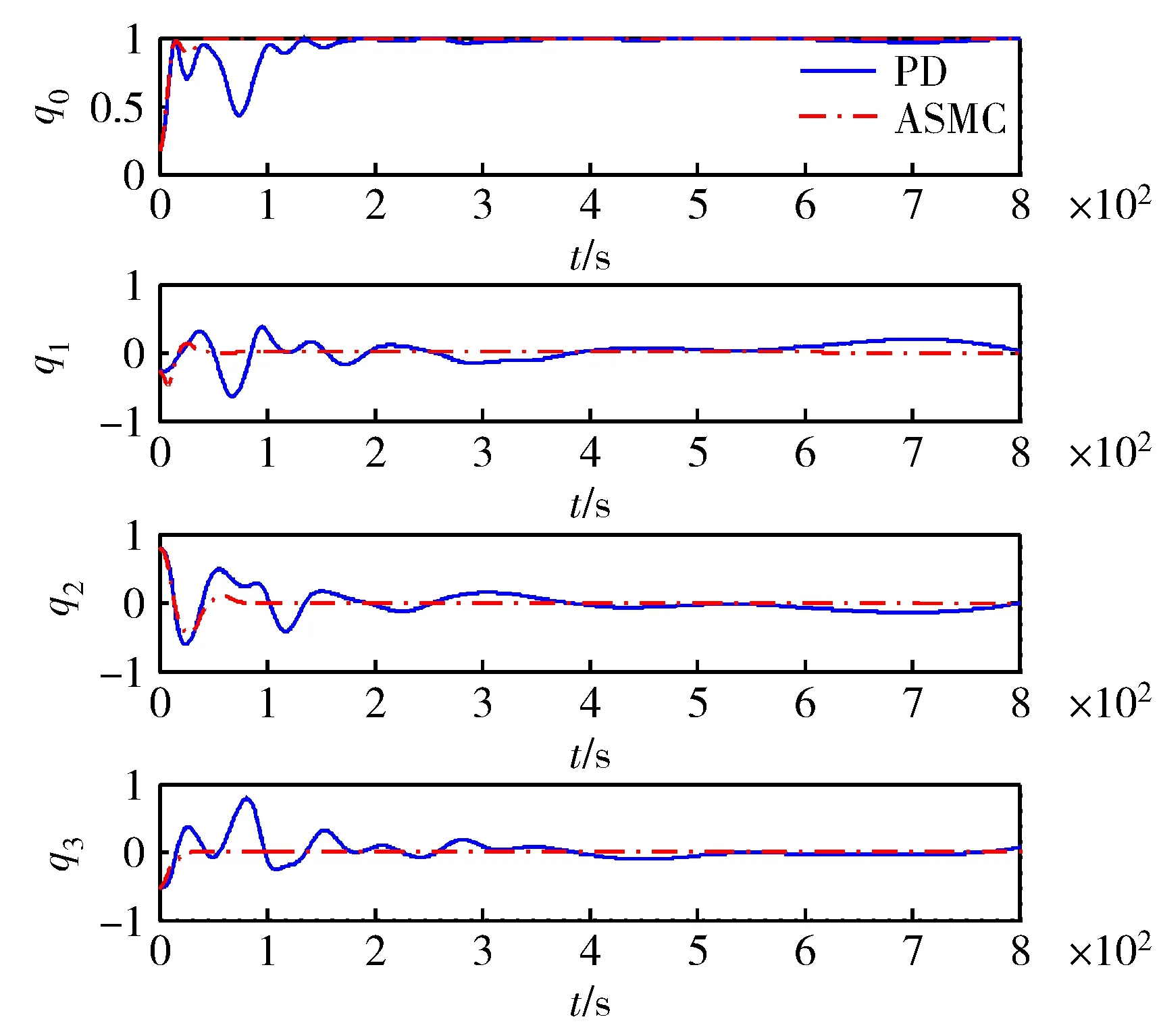
图3 故障情况下姿态四元数响应曲线

从图2和图3可以看出，在执行器饱和约束条件下，尽管动量轮存在部分失效或者卡死的情况，由于引入了变结构控制和自适应律，仍能实现对卫星姿态的控制，对干扰具有较强的抑制能力，收敛时间也明显快于PD控制。

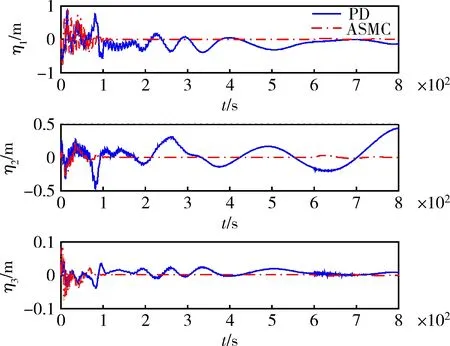
图4 故障情况下振动模态响应曲线

图5 飞轮输出力矩响应曲线

图4表明相对于传统的PD控制，利用本文设计的方法，能有效抑制模态的振动，同时利用应变反馈速率补偿器避免了轨控期间挠性模态的常值形变，而传统的PD控制对于轨控期间的挠性卫星而言，模态振动很难得到抑制。

4 结论

本文针对轨控期间挠性卫星姿态控制系统，研究在执行器故障、轨控推力及推力偏心造成影响及饱和约束情况下的容错控制问题。通过设计变结构自适应控制，实现卫星姿态角度、角速度和模态的收敛。设计的容错控制器不需要故障信息，容错控制器简单，需要调节的参数少，易于实现。最后通过仿真比较，结合轨控期间的挠性卫星姿控系统，验证了本文提出的变结构容错控制方法在飞轮故障、干扰和输入饱和约束情况下的有效性。

[1] 陈雪芹，耿云海，张迎春.基于LMI的鲁棒容错控制及其在卫星姿态控制中的应用[J].控制理论与应用,2008,25(1)：95-99.(CHENXue-qin,GENGYun-hai,ZHANGYing-chun.RobustFault-tolerantH-infinityControlBasedonLMIApproachandApplicationinSatelliteAttitudeControlSystem[J].ControlTheroyandApplications,2008,25(1):95-99.)

[2]JinJaehyun,KoSangho,RyooChang-Kyung.FaultTolerantControlforSatellitewithFourReactionWheels[J].ControlEngineeringPractice,2008,16:1250-1258.

[3]CaiWC,LiaoXH,SongYD.IndirectRobustAdaptiveFault-tolerantControlforAttitudeTrackingofSpacecraft[J].JournalofGuidanceandDynamics, 2008,31(5):1456-1463.

[4]LiangYew-Wen,XuSheng-Dong,TingLi-wei.T-SModel-basedSMCReliableDesignforaClassofNonlinearControlSystems[J].IEEETransactionsonIndustrialElectronics, 2009, 56(9):3286-3295.

[5] 程月华,姜斌,孙俊,樊雯.基于滑模观测器的卫星姿态控制系统滑模容错控制[J].上海交通大学学报,2011,45(02):190-194.(CHENGYuehua,JIANGBin,SunJun,FANWei.SlidingModeFaultTolerantControlforSatelliteAttitudeSystemsBasedonSlidingModeObserver[J].JournalofShanghaiJiaotongUniversity,2011,45(02):190-194.)

[6]ChengYuehua,JiangBin,FuYanping.ObserverBasedReliableControlforSatelliteAttitudeControlSystemswithSensorFaults[J].InternationalJournalofInnovativeComputing,Information&Control,2011,7(7B):4149-4160.

[7] 肖冰，胡庆磊，马广富.基于观测器的航天器执行机构失效故障重构[J].宇航学报,2011,32(2):323-328.(XIAOBing,HUQinglei,MAGuangfu.ObserverBasedFaultReconstructionforSpacecraftunderLossofActuatorEffectiveness[J].JournalofAstronautics,2011,32(2):33-328)

[8]GaoZhifeng,JiangBin,ShiPeng,etal.SensorFaultEstimationandCompensationforMicrosatelliteAttitudeControlSystems[J].InternationalJournalofControl,AutomationandSystems,2010, 8(2):228-237.

[9] 欧阳高翔,倪茂林,孙承启.视故障为结构不确定项的鲁棒可靠跟踪控制器设计[J].控制理论与应用,2009,26(01):80-84.(OuyangGao-xiang,NIMao-lin,SUNCheng-qi.RobustReliableTrackingControllerDesignwhentheFaultisViewedasaStructuralUncertainty[J].ControlTheroyandApplication,2009,26(01):80-84.)

[10]YeJiang,HuQinglei,MaGuangfu.AdaptiveBackstepingFaultTolerantControlforFlexibleSpacecraftwithUnknownBoundedDisturbancesandActuatorFailures[J].ISATransactions, 2010,49(1):57-69.

[11] 刘莹莹,周军.挠性卫星轨控期间动力学与姿态控制[J].空间控制技术与应用，2008,34(2):9-13.(LIUYingying,ZHOUJun.DynamicsandAttitudeControlofFlexibleSatelliteDuringOrbitalManeuver[J].AerospaceControlandApplication,2008,34(2):9-13.)

[12] 周文忠.地球同步卫星近地点变轨期间的三轴姿态稳定[J].航天控制, 1993,11(2):7-15.(ZHOUWenzhong.ThreeAxesAttitudeStabilizationofGeostationarySatelliteduringApogeeOrbitManeuvering.AerospaceControl,1993,11(2):7-15.)

[13] 张娴，程月华，姜斌.轨控期间挠性卫星姿控系统的容错控制[J].航天控制,2011,29(1):41-47.(ZHANGXian,CHENGYuehua,JiangBin.AdaptiveBacksteppingFault-tolerantControlforFlexibleSatelliteAttitudeControlSystemduringOrbitControl[J].AerospaceControl,2011,29(1):41-47.)

[14]ImranAli,GianmarcoRadice,JongraeKim.BacksteppingControlDesignwithActuatorTorqueBoundforSpacecraftAttitudeManeuver[J].JournalofGuidance,Control,andDynamics, 2010, 33(1):254-259.

[15] 高岱，吕建婷，王本利.考虑控制输入受限的卫星姿态控制[J].哈尔滨工业大学学报，2010,42(5):683-685.(GAODai,LVJianting,WANGBenli.SatelliteAttitudeRegulationControlSubjecttoControlInputSaturation[J].JournalofHarbinInstituteofTechnology,2010,42(5):683-685.)

[16] 姜野，胡庆雷，马广富.控制输入饱和的挠性航天器姿态机动智能鲁棒控制[J].宇航学报，2009,30(1):188-193.(JIANGYe,HUQinglei,MAGuangfu.IntelligentAdaptiveVariableStructureAttitudeManeuveringControlforFlexibleSpacecraftwithActuatorSaturation[J].JournalofAstronautics,2009,30(1):188-193.)

[17]Boiskovi′cJovanD,LiSai-Ming,etal，RobustAdaptiveVariableStructureControlofSpacecraftUnderControlInputSaturation[J].JournalofGuidance,Control,andDynamics, 2001, 24(1):14-22.

[18]GuanWei,YangGuang-Hong.AdaptiveFaultTolerantControlofLinearTime-invariantSystemsSubjecttoActuatorSaturation[C].ControlandDecisionConference,CancunMexico, 2008.

Fault-tolerant Control Under Constrained Input for Flexible Satellite Attitude Control System during Orbit Control

FU Yanping1CHENG Yuehua1，2JIANG Bin1

1. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China2. Academy of Frontier Science, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Duringorbitcontrolforaflexiblesatellite,largedisturbancetorquemaybecausedbythemisalignments,whichwouldaffectthesatellites’attitudedirectly.Besides,actuatorscanjustprovidelimitedtorquebecauseofphysicalproperty.Andinputsaturationshouldbeconsideredtoguaranteethesystemstability.Inthispaper,withactuatorfaultandtheproblemsmentionedaboveconsidered,weproposeatolerantcontrolmethodbasedoninputsaturationforflexiblesatelliteattitudecontrolsystem.Finallytheperformanceoftheproposedfaulttolerantcontrollerisdemonstratedvianumericalsimulationforflexiblesatelliteduringorbitcontrol.

Flexiblesatellite;Variablestructure;Inputsaturation;Reactionwheelfault

*国家自然科学基金(61034005);江苏省自然科学基金(BK2010072)资助

2011-12-22

傅艳萍(1986-)，女，云南人，硕士研究生，主要研究方向为小卫星姿态控制、故障诊断与容错控制；程月华(1977-)，女，安徽人，博士研究生，主要研究方向为小卫星姿态控制、故障诊断与容错控制；姜 斌(1966-)，男，江西人，教授，主要研究方向为故障诊断及容错控制。

V448.22+1

A

1006-3242(2012)03-0038-07