基于遗传算法的共形阵副瓣电平抑制研究
范忠亮
(中国电子科技集团公司38所,合肥230088)
0 引 言
先进的飞行器,如导弹、飞机、卫星等,将携带的电子设备的天线单元安装在飞行器表面,使阵面与飞行器表面相吻合,构成共形阵列天线,可保证飞行平台良好的气动外形,获得更高的武器性能,提升雷达平台的隐身性能[1]。同平面阵相比,共形阵与载体平台共形,可以不破坏载体平台的机械结构,有效利用平台空间。以色列的Phalcon(Phased Array L-band Conformal)预警机就是使用共形阵列的典型代表。然而共形阵方向图具有较高的副瓣电平,导致抗截获、抗干扰能力较差。
目前共形阵副瓣电平优化设计主要基于统计模型算法,如遗传算法(GA)和模拟退火算法等[2-5]。由于GA在统计算法中具有可操作性强、能避免早熟及陷入局部最优解等问题,因此在天线方向图优化设计中得到了广泛应用[6-7]。本文针对波束扫描范围有限的应用场合,提出了一种基于遗传算法的共形阵副瓣电平抑制方法。在不同的扫描位置,保证天线孔径不变,以副瓣电平最小为适应度函数,通过遗传算法控制共形阵列的开关矩阵,有效改善了共形阵列的副瓣电平,提高了阵列优化效率。
1 系统模型
在波束扫描范围有限的应用中(如天对地雷达系统),可使用弧形天线阵形成共形天线阵,如图1所示。
图1中,全向天线单元均匀分布在半径为R的圆弧AB上,相邻2个天线单元之间圆弧夹角为θ,第0个天线单元和第k个天线单元之间圆弧夹角为θk。
当目标在如图1所示的γ方向时,第i个天线单元与第0个天线单元之间的空间波程差Di为:
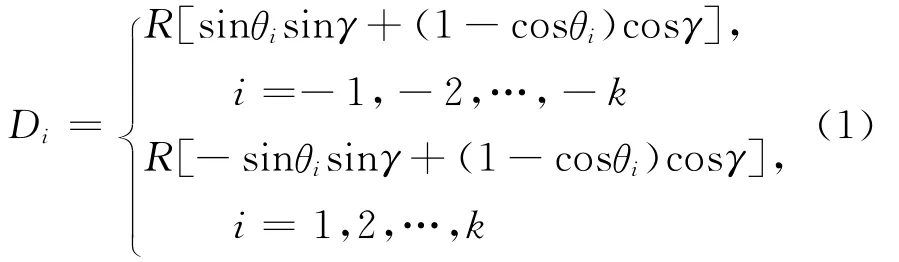
考虑到圆阵半径R与相邻天线单元之间的圆弧间距dc及圆弧夹角θ的关系为:

则第i个天线单元与第0个天线单元之间的空间相位差为:

每个单元通道中的移相器按式(3)进行相应的移相,控制每个天线阵元的阵内相位差抵消掉空间相位差,即可实现共形阵天线波束扫描。当天线主瓣指向为γ0、不考虑幅度加权时,天线方向性函数可以表示为:
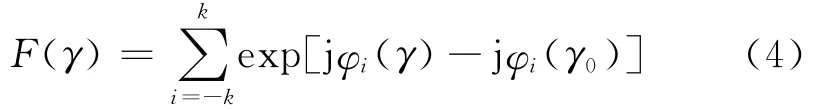
2 副瓣电平抑制算法
图1所示的共形阵天线方向图副瓣电平较差,需要采用优化算法进行优化。在保证天线孔径不变的情况下,本文提出了基于GA的副瓣电平抑制方法。
GA是借鉴生物的自然选择和遗传进化机制开发出的全局优化自适应概率搜索算法。GA一般是从一个初始群体开始,根据适应度函数评价每个个体优劣,经过选择、交叉、变异操作,产生新一代群体,群体经一代代进化,直至达到给定的精度或遗传代数。它是只需要利用评价函数信息的随机优化自适应方法,适用于不连续、强参数约束和有多个局部极值的高维问题。基于GA的副瓣电平抑制方法的流程图如图2所示。

图2 GA流程图
2.1 编码及初始种群设置
设第G代种群SG为:

式中:染色体sGl为2k+1维列向量,每个元素sGl(i)的取值为0或1,其中l=1,2,…,L,i=-k,-k+1,…,k,L为种群规模。
在GA算法的输入中,采用均匀分布的0,1序列生成集合S0,即s0l(i)∈ {0,1},且取0和取1的概率相等。
2.2 适应度函数
利用染色体控制天线开关矩阵来抑制副瓣电平,则染色体sGl对应的天线方向图为:

取副瓣电平最大值作为适应度函数,即:
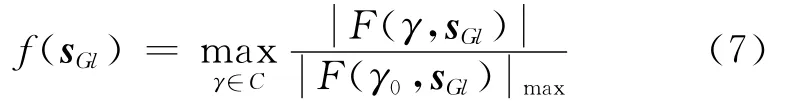
式中:C为方向图的旁瓣扫描角集合。
因此,旁瓣电平最优化问题可表示为求解如下优化问题,即 min[f(sGl)]。
2.3 选择
本文基于轮盘赌法则来选择染色体,具体过程如下:
(1)根据种群中每个染色体的适应度函数值计算每个染色体sGl被选中的概率ql,即ql=
(2)计算累计概率
(3)生成[0,1]之间均匀分布的随机数r1,若pl-1<r1≤pl,则选择sGl为G+1代种群中的一个染色体;
(4)重复L次第(3)步,遍历当代种群中的所有染色体。
2.4 交叉
利用单点交叉算法实现相邻染色体之间的交叉。从l=1到L执行如下操作:生成[0,1]之间均匀分布的随机数r2,若r2大于交叉概率pc,选择当前染色体sGl和第G代种群中的任意一个染色体,以均匀分布随机选择染色体的交叉位置进行单点交叉。
2.5 变异
以变异概率pm在经过交叉的种群中依次选择染色体的每个基因进行基因变异。其过程为:依次选择每个染色体的基因,生成[0,1]之间均匀分布的随机数r3,若r3大于pm,则该染色体的基因进行突变,即0变为1或1变为0,否则基因保持不变。为了保证当前最优解存在于下一代种群中,将第G带的最优解直接选入第G+1代。
重复执行选择、交叉、变异操作形成新的种群,直到完成给定循环次数或者满足一定结束条件,GA算法输出最优染色体后结束。为了保证天线孔径不变,GA算法中保持sGl(-k)=sGl(k)=1,即弧形天线阵的两端天线始终开启。虽然该方法是针对一维阵列的优化算法,但是通过简单的推导,可以很容易地扩展到二维阵列中。
3 数值仿真
取天线单元总数为41(即k=20),相邻天线单元之间的圆弧夹角为6°,扫描频率为8GHz,圆阵半径为0.5m。以均匀分布建立初始种群,初始种群规模L为80,交叉概率pc取0.8,变异概率pm取0.05,传代数上限为200。
图3和图4分别对扫描角为0°和30°2种情况下,本文算法对副瓣电平的改善情况进行了比较,图中无稀疏情况代表使用GA前共形阵的方向图,稀疏情况代表使用GA后共形阵的方向图。从图3和图4可以看出,本文算法在2种扫描角情况下,副瓣电平都得到了改善,改善量分别为4.410 9dB和3.673 3dB。此外可以看出,随着扫描角的增大,副瓣电平的改善量逐渐减小。
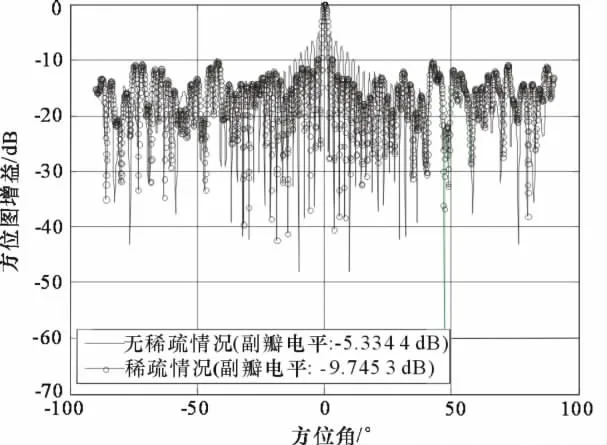
图3 波束指向为0°时,稀疏前和稀疏后的方向图比较

图4 波束指向为30°时,稀疏前和稀疏后的方向图比较
图5和图6为2种扫描角情况下,最佳适应度函数随遗传代数的变化。
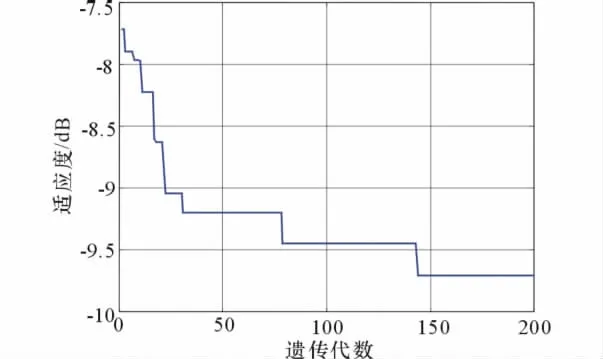
图5 波束指向为0°时最佳适应度函数变化曲线
从图5和图6可以看出,2种情况在初始迭代时都有较快的收敛趋势,并且2种情况在迭代180次以后都达到了稳定收敛,相比全搜索所需的迭代次数239,基于GA的优化算法具有很高的阵列优化效率。此外,对比图5和图6,在小扫描角(即扫描角为0°)情况下,本文算法可以更快地达到收敛。
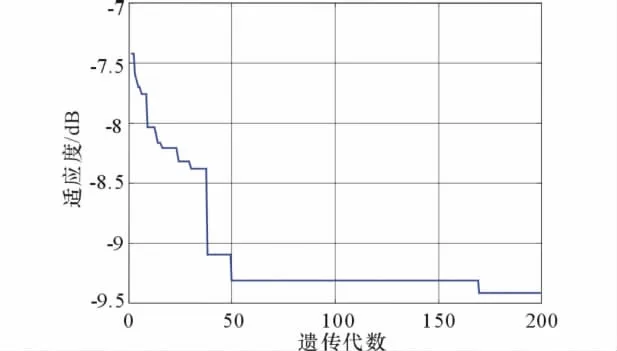
图6 波束指向为30°时最佳适应度函数变化曲线
图7和图8分别为优化后天线布置示意图。
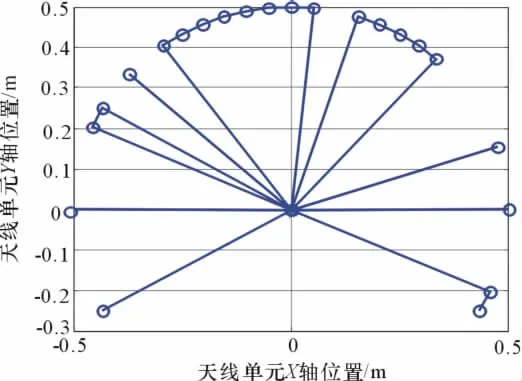
图7 波束指向为0°时天线布阵优化结果
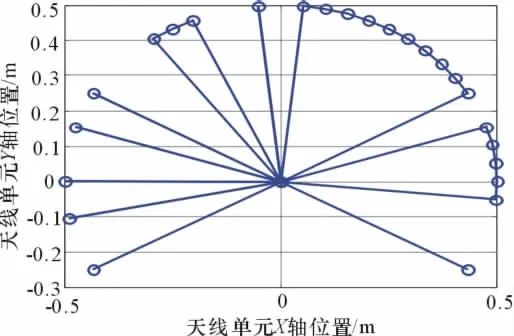
图8 波束指向为30°时天线布阵优化结果
4 结束语
共形阵副瓣电平优化是非线性全局寻优问题。本文利用遗传算法概率搜索、最优解不依赖初始值等特点,通过控制阵列开关矩阵,针对扫描角度有限的共形阵列提出了一种降低副瓣电平的方法。仿真结果表明,遗传算法具有较高的求解效率,可以有效降低共形阵天线的副瓣电平,提升优化效率。
[1]Sureau J C.Conformal arrays come of age[J].Microwave Journal,1973(10):23.
[2]Petko J S,Werner D H.The evolution of optimal linear polyfractal arrays using genetic algorithms[J].IEEE Transactions on Antennas and Propagation,2005,55(11):3604-3615.
[3]Allard R J,Werner D H,Werner P L.Radiation pattern synthesis for arrays of conformal antennas mounted on arbitrarily-shaped three-dimensional platforms using genetic algorithms[J].IEEE Transactions on Antennas and Propagation,2003,51(5):1054-1062.
[4]Bray M G,Werner D H,Boeringer D W.Optimization of thinned aperiodic linear phased arrays using genetic algorithms to reduce grating lobes during scanning[J].IEEE Transactions on Antennas and Propagation,2002,50(12):1732-1742.
[5]Chen K,Yun X.Synthesis of sparse planar arrays using modified real genetic algorithm[J].IEEE Transactions on Antennas and Propagation,2007,55(4):1067-1073.
[6]崔兵伟,陈客松.运用遗传算法优化共形球面天线阵列[J].中国雷达,2009(2):46-49.
[7]杨继波,李会勇,陈客松,等.球面共形天线阵列的稀布优化算法[J].西安交通大学学报,2011,45(4):77-81.

