基于双/多基地雷达的抗分布式干扰效果研究
何叶飞,刘宗福,刘岩磊
(解放军92785部队,秦皇岛066200)
0 引 言
分布式干扰[1]是近几年才出现的新的干扰样式,分布式干扰的特点是分布的空域广,干扰面积大,干扰强度高。对于分布式干扰对雷达系统干扰效果的研究,国外文献报道比较少,国内学者做过一些研究。文献[2]比较了分布式干扰机对单/双基地雷达进行不同数量的主瓣干扰和旁瓣干扰的效果。文献[3]推导了对双基地雷达进行分布式压制性干扰的数学模型,分析了分布式干扰下各种干扰情况对双基地雷达探测能力的影响。在双基地雷达抗干扰方面,文献[4]给出了双基地雷达探测区和干扰暴露区的计算模型,分析计算了在自卫式干扰和远距离支援干扰条件下的双基地雷达抗有源压制性干扰性能,并与单基地雷达情况进行了比较。对于如何抗分布式干扰,尤其是分布式干扰机数量比较多的情况下,目前还没有见到文献研究过,这也是一个亟待解决的问题。
由于双基地雷达系统[5]的发射站和接收站可远距离分置,且接收站是无源的,因而有较好的抗干扰能力。本文提出了一种通过在单基地雷达两边部署接收站,与原来单基地雷达构成双/多基地雷达来抗分布式干扰的方法。从双基地雷达方程和干扰方程出发,探讨了分布式干扰下单基地雷达和双/多基地雷达威力范围,通过数据分析得出了一些有意义的结论。
1 双基地雷达抗分布式干扰模型
针对分布式干扰离雷达距离近的特点,在单基地雷达旁边部署接收站,与单基地雷达组成双基地雷达。在没有受到干扰时,系统处于正常的单基地雷达方式,当遇到分布式干扰使得单基地雷达致盲时,就把单基地雷达当做照射站,和部署在旁边的接收站一起组成双基地雷达系统进行工作。由于接收站不辐射电磁波,敌方施放干扰只是针对照射站的,这样可以达到抗干扰的目的。图1是单基地雷达旁边部署接收站而形成的双基地雷达示意图。

图1 双基地雷达极坐标图
下面分析上述模型的双基地雷达方程。
如图1所示的双基地雷达组成结构,其在一定虚警概率和检测概率下的作用距离是探测系统性能的重要指标,无干扰情况下,考虑方向图、传播因子和损耗因子的影响后,由双基地雷达工作原理可推导出双基地雷达方程[4]:

压制性噪声干扰的作用是以噪声功率阻塞雷达接收机使其失去工作能力,干扰机对双基地雷达接收机形成的干扰功率谱密度J0为:

对双基地雷达有:

式中:PJ为干扰机发射功率;GJ为干扰机天线增益;GR为雷达接收天线的功率增益;BJ为干扰机带宽;LJ为干扰机的系统损耗;(RTRR)j为干扰条件下双基地雷达的作用距离积;KB为无干扰条件下双基地雷达的作用距离积;KBJ为干扰下双基地雷达的作用距离积;K为波尔兹曼常数(其值为1.38×10-23WS/°);TS为接收机的噪声温度。
2 双/多基地雷达抗分布式干扰效果研究
2.1 问题描述
由于接收站不辐射能量,敌方释放分布式干扰往往是针对照射站。假设分布式干扰分布在照射站前方,此时,单基地雷达和双基地雷达的作用距离都变小。由于分布式干扰离照射站距离近,对单基地雷达的干扰强度大,单基地雷达可能完全致盲。而分布式干扰离接收站比较远,分布式干扰对双基地雷达的干扰效果就比较小,因此,分布式干扰使单基地雷达致盲区域可以通过双基地雷达进行补盲。
假设模型中双基地雷达基线长度为L,距离积KB=10 000km2,KTS=6×10-21,雷达接收天线的功率增益为GR=20dB,波长λ=0.1m,主瓣宽度θ0.5=13°。分布式干扰条件下,假设n个性能完全相同的分布干扰单元,其发射功率为PJ=-30dBm,干扰机天线增益为GJ=5dB,干扰机带宽为BJ=1 07H z,干扰机的系统损耗为LJ=2dB,第i个干扰机垂线与雷达接收机天线之间的距离为R=20km,主瓣宽度θi0.5=20°。
假设有m部干扰机位于发射机上空20km,分布范围宽度为20km,干扰机的主瓣指向与干扰机与发射机连线的夹角φi服从0到2π的均匀分布,下面将分析分布式干扰下双基地雷达与单基地雷达威力范围比较,通过比较证明双基地雷达抗分布式干扰的效果。
2.2 分布式干扰条件下1个接收机的双基地雷达
与单基地雷达威力范围比较
根据所给的问题描述的条件,分别对干扰机数目m=3 0,5 0,1 0 0对应双基地雷达的基线l=30km,50km和100km时进行仿真,结果如图2所示,图中m为分布式干扰机数目,l为双基地雷达基线长度。
图2中正圆区域为无干扰情况下双基地雷达的威力范围,扇形区域为干扰情况下单基地雷达的威力范围,扇形中心和椭圆交点为发射机接收机的位置,扇形中心上方点为分布式干扰机位置,椭圆区域为干扰情况下双基地雷达的威力范围,从图中可以看到效果很明显。

图2 双基地雷达补盲效果图
2.3 分布式干扰下2个接收机的多基地雷达与单基地雷达威力范围比较
根据所给的问题描述的条件,分别对干扰机数目m=30,50,100对应多基地雷达的基线l=30 km,l=50km和l=100km时进行仿真,结果如图3所示,图中m为分布式干扰机数目;l为双基地雷达基线长度。
图3中正圆区域为无干扰情况下单基地雷达的威力范围,扇形区域为干扰情况下单基地雷达的威力范围,扇形中心和椭圆交点为发射机接收机的位置,扇形中心上方点为分布式干扰机位置,椭圆区域为干扰情况下多基地雷达的威力范围,从图中可以看到效果很明显。
3 数据分析
由于在仿真过程中假设每个干扰机的主瓣与干扰机和发射机连线的夹角为一个在0到2π范围内均匀变化的值,因此即使参数一样,每次的仿真结果也肯定不同,但是误差也会在一定的范围内,通过比较可以得出上述结论。
这里定义雷达盲区系数为:雷达在干扰环境下较无干扰条件下减少的探测范围与雷达在无干扰条件下探测范围之比,它是一个小于等于1的数,也可以用百分数表示。
双/多基地雷达补盲系数为:双基地雷达与单基地雷达在干扰情况下减少的探测范围与单基地雷达在干扰环境下减少的探测范围的差值与单基地雷达在干扰条件下减少的探测范围之比,它是一个小于等于1的数,也可以用百分数表示。

图3 多基地雷达补盲效果图
由仿真结果得出多基地雷达的盲区系数和补盲系数如表1所示。
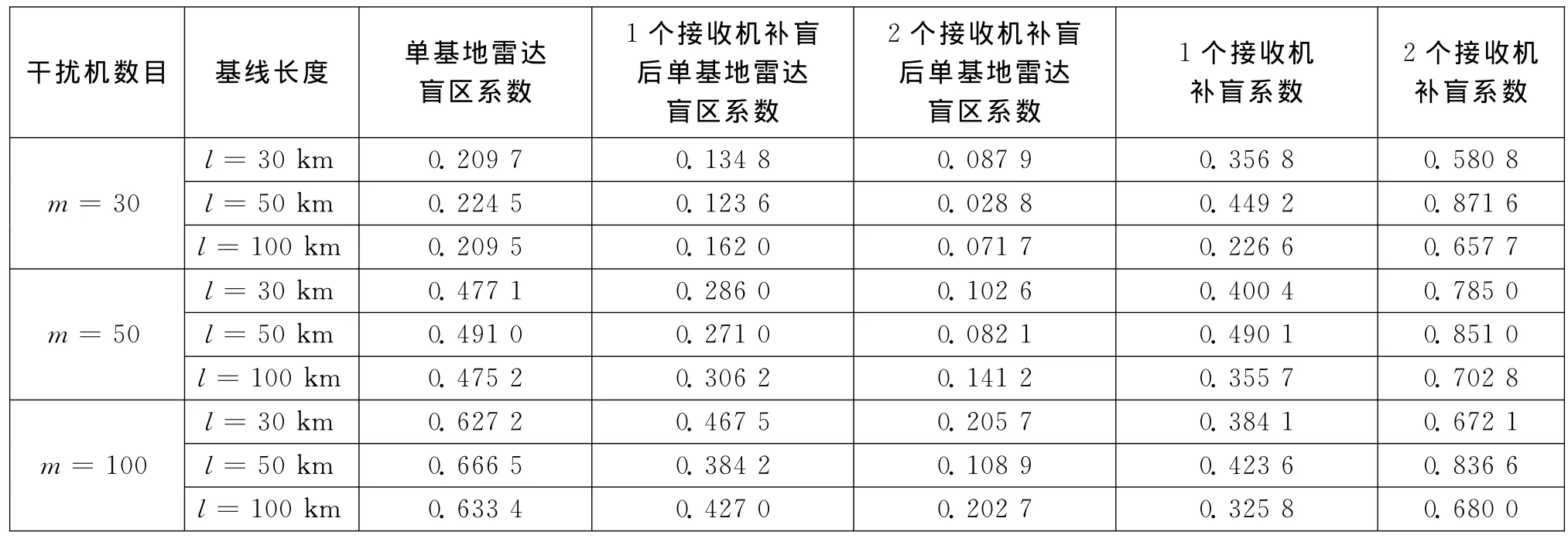
表1 双/多基地雷达的盲区系数与补盲系数
从表1可以看出,随着干扰机数目的增多,由于总功率的增大,单基地雷达的盲区系数在增大,双多基地雷达的盲区系数也在增大。而双多基地雷达的补盲系数与干扰机的数目关系不大,通过表中的数据可以看出,当干扰机数目一定时,对于不同的基线长度,双/多基地雷达的补盲系数不同,但是可以看出,l=50km时的补盲系数大于l=30km和l=100km时的补盲系数,所以可以得出结论:双多基地雷达的补盲效果与其基线长度有关,基线长度影响其补盲效果好坏。当l=50km时的补盲效果明显好于l=30km和l=100km时的补盲效果,基线越长或越小都使其补盲效果减小,因此基线的长度必须适当,可以确定在l=30km和l=100km之间存在一点(不一定是l=50km),在这点双/多基地雷达的补盲效果达到最好。
4 结束语
本文提出一种通过在单基地雷达两边部署接收站,与原来单基地雷达构成双/多基地雷达来抗分布式干扰的模型。对分布式干扰下双基地雷达的雷达方程进行了分析,画出了分布式干扰下单基地雷达和双/多基地雷达的威力范围,利用盲区系数和补盲系数两个评价指标,得出了不同情况下双基地雷达的抗干扰效果,得出了一些有意义的结论。这些结论对雷达抗分布式干扰,以及双基地雷达部署有一定的参考价值。
[1]田波,张永顺.发展中的分布式干扰技术[J].航天电子对抗,2004(1):41-43.
[2]王国宏,王捷,倪保航.“狼群”干扰对单/双基地雷达的干扰分析[J].海军航空工程学院学报,2005,3(20):311-314.
[3]王勇刚,李修和,沈阳.分布式压制性干扰下的双基地雷达探测能力研究[J].电子信息对抗技术,2007,4(22):45-49.
[4]高彬,吕善伟,郭庆丰.双基地雷达抗干扰模型的研究[J].现代防御技术,2006(2):61-64.
[5]杨振起,张永顺.双(多)基地雷达系统[M].北京:国防工业出版社,1998.

