地对空干扰站有效干扰区域分析
张敬博,秦开兵,康亚光
(1.空军预警学院,武汉430019;2.解放军61251部队,秦皇岛066000)
0 引 言
未来高科技局部战争中,我方地面军事、政治、经济等重要目标可能成为敌方的重点攻击对象。为了有效保护目标免受敌方攻击,就需要合理部署电子对抗力量。如果敌方目标批次较多,我方在干扰方向上一对一的干扰力量不足的情况很有可能出现,因此,必须掌握单部干扰站的实际干扰空间并结合侦察到的敌方信息,综合判断是否可以对敌方实施有效压制干扰,并进行战术调整,达到最佳干扰效果。
1 干扰机天线在雷达方向上增益的计算[1,2]
理想情况下,干扰波束的中心应该瞄准敌机载雷达方向,也就是说干扰波束的最大增益方向对准敌机载雷达。然而在实际作战操作中,从我方发现目标进行上报,到中心指挥所做出判断下达作战命令,继而干扰各站开始执行操作,整个过程中会出现诸如装备本身产生的以及系统延迟产生的误差。因此干扰机天线指向雷达方向与干扰波束中心轴方向存在一定夹角。
在图1中,用φ表示干扰机天线指向雷达方向与干扰波束中心轴方向的夹角。图1(a)表示理想情况下干扰机天线增益方向(即φ=0°),图1(b)表示干扰机天线最大增益方向没有对准敌机(即φ≠0°),因此干扰机天线在雷达方向上的增益Gj应该用G′j(φ)来代替。
图2中以目标中心到干扰机位置连线方向为x轴方向,以地面为xy平面。图2(a)中敌机位置为A点,干扰机位置为J,目标中心为O,A′为敌机在地面上的投影,αV、αH分别为飞机相对于目标的仰角和方位角。图2(b)中βH为干扰主瓣中心轴在地面上的投影与x轴的夹角,βV为干扰主瓣中心轴在垂直平面上的俯仰角,φH为该投影与雷达和干扰机连线在地面投影的夹角。由图2容易得到:
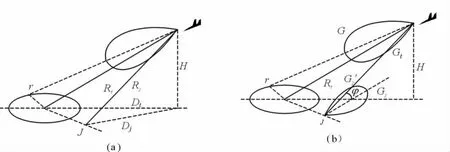
图1 理想情况与存在φ时的干扰机天线增益比较
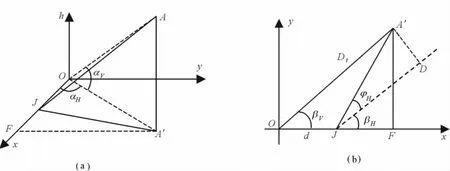
图2 几何关系图

再以干扰机J为原点,建立如图3所示坐标系,JB为干扰波束中心指向,JA为干扰机与飞机(雷达)的连线,φ=∠AJB,则:

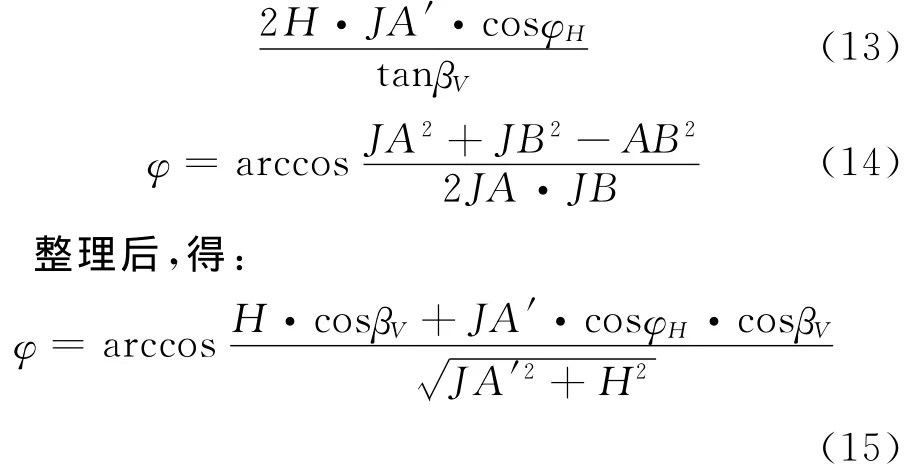

图3 以干扰机为原点的坐标关系图
干扰机天线在雷达方向上的增益由经验公式得:

式中:b为干扰波束主瓣的零功率半波束宽度。
2 干扰方程[1-3]
干扰方程是表征雷达接收机输入端干扰信号增强到恰好淹没目标回波信号状态的等式。
首先考察敌机接收机输出端的目标回波信号功率。根据雷达方程,雷达接收到的目标回波信号功率Prs为:

雷达接收到的干扰机干扰压制信号功率Prj为:
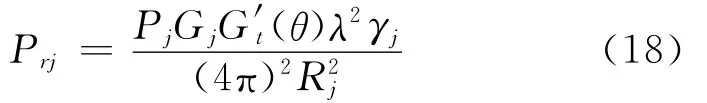
考虑单部干扰机实施干扰的情况可以得:

式中:Kj为外压制系数。
将公式(17)和公式(18)代入公式(19),整理后得:

考虑φ的影响后,公式(20)中不等式左边变为:

3 仿真实例及结论[4]
干扰压制区的解析计算中含有超越方程,因此采用步进法推测计算有效干扰区。根据前面建模的结果,需要对φ取值进行讨论。

3.1 取φ=0°的情况
该种情况下,干扰机最大增益方向始终对准敌机雷达,因此只需考虑θ,且能够对全方位上的干扰压制区进行计算(以α和Dt为步进量)。仿真后可得图4,在图4中"8"字形为干扰压制区,"·"为干扰机所在位置。

图4 干扰机保护地面目标的有效干扰区
3.2 取φ≠0°的情况
该种情况下,雷达天线增益角θ和干扰天线增益角φ均不为零,无法确保干扰增益最大方向对准敌机,因此必须考虑垂直方向的分量,且只能对固定干扰波数内的压制区域进行计算(以αV、αH和Dt为步进量)。在图4的参数基础上增加kj=0.0 5,φ0.5=10°,b=15°,设飞机的最高飞行高度Hmax=15km、水平最大距离80km为规定区域范围,推导干扰波束方向固定时、空间上的有效干扰区。
分别假设βV,βH为不同值时,即干扰机天线波束指向不同时,对固定波束内压制区进行仿真。仿真结果如图5~图8。图中粗实线为干扰波束中心最大增益方向;“·”为干扰站所在位置;(0,0,0)点为目标中心位置;“×”标记(60,3,5)点设置1部敌机;细线条为有效压制区边界,形状近似为漏斗,其内部区域为有效压制区,外部为暴露区。设置干扰波束中心轴水平和垂直方向夹角逐渐增大,得到4幅有效压制区仿真区域图,通过计算可以得到假设敌机φ 值分别对应为φ1=6.7°、φ2=9.9°、φ3=8.7°、φ4=11.3°、φ5=14.7°,均小于15°,即全部位于干扰波束内。
对4张仿真图仔细观察后可以发现:
(1)干扰效果最好的区域基本位于干扰主波瓣半功率点以内;干扰压制区近似形状为锥形;
(2)干扰天线主波瓣最大增益方向的水平夹角βV越大,干扰压制区底部压制区收缩越明显,干扰效果越差;
(3)整体干扰压制区形状随βV、βH角度的增加越发不规则。对比4张图中“×”标记敌机位置可以看出,图5、6、7、8中敌机均处于有效压制区范围内。通过进一步仿真后可以发现,当垂直与水平角度均达到20°左右时在规定范围内无法绘制干扰压制区,即无法有效干扰。

图5 βH=0°,βV=0°时波束内有效干扰区仿真
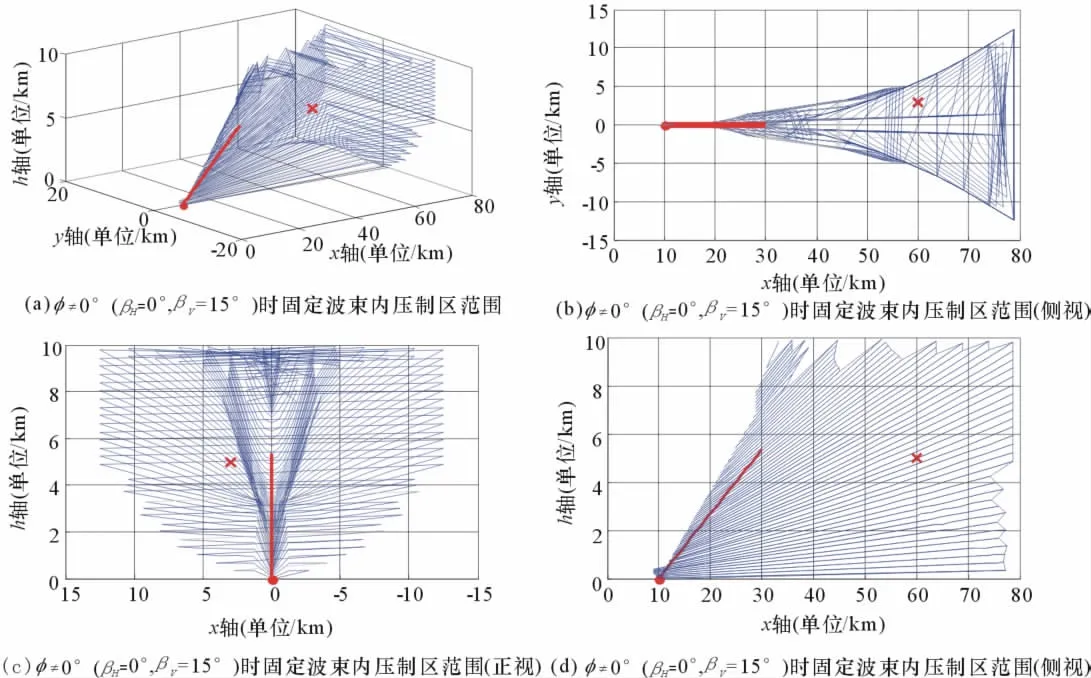
图6 βH=0°,βV=15°时波束内有效干扰区仿真
分析产生干扰压制区形状不规则的原因之一应为在建模过程中同时考虑了雷达天线和干扰天线的天线增益夹角,同时又都采用了经验公式进行计算,所以角度和增益的变化关系并不是线性关系。因此,如果在我方干扰天线方向增益图已知,甚至敌方雷达天线方向增益图已知的情况下,用来代替经验公式对增益进行计算,仿真结果将更贴近实际。
4 结束语
通过对单个波束内的有效干扰区域仿真以及对结果进行的简单分析,得到了单站有效干扰区的空间三维区域模型,为实际作战过程中可能出现的干扰资源分配情况提供了具体的理论依据。

图7 βH=10°,βV=0°时波束内有效干扰区仿真

图8 βH=15°,βV=15°时波束内有效干扰区仿真
[1]邵国培.电子对抗作战效能分析[M].北京:解放军出版社,1998:139-144.
[2]罗景青.雷达对抗原理[M].北京:解放军工业出版社,2003:274-277.
[3]王国玉,汪连栋.雷达电子战系统数学仿真与评估[M].北京:国防工业出版社,2004.
[4]丁劲,胡凌云,李柔刚.地对空雷达对抗仿真系统的研究与实现[J].舰船电子对抗,2004,27(6):39-42.

