基于核熵成分分析的热轧带钢自适应聚类分析
何飞,徐金梧,梁治国,王晓晨
(北京科技大学 国家板带生产先进装备工程技术研究中心,北京,100083)
带钢热连轧生产过程需要保证的质量有:(1) 尺寸形状质量:厚度精度、宽度精度、凸度及平直度等;(2) 表面质量:划痕、裂纹等;(3) 力学性能质量:屈服强度、抗拉强度、伸长率等[1]。尺寸形状质量可以由厚度测试仪、多功能凸度仪等测量得到。随着高速工业拍摄技术的发展,基于机器视觉技术的表面质量在线检测系统可以有效地在线测量表面质量状况。力学性能则必须通过离线采样的方式获取。随着计算机控制技术和传感技术的发展,大量生产过程控制和实测数据被记录,为生产过程和质量的分析提供了真实的数据来源[2-4]。目前利用统计回归分析方法对带钢力学性能进行预报的研究,也取得了一些研究成果,但通常需要大量实际生产数据,而且预测精度不高,难以应用于实际生产过程。拟通过聚类方法对生产过程数据进行分析,事先了解生产状态,对聚类性较差的数据进行重点的力学性能检测。聚类分析前常需要对数据进行处理[5],通常包括特征选择和特征提取,常用的特征选择方法有向前选择、向后选择、逐步选择等,但无法提取特征间的关系。主成分分析、独立成分分析等作为常用的特征提取方法,可以有效提取特征间的线性关系[6]。而在实际生产中,数据间往往呈现复杂的非线性关系,核函数的引入可以有效解决变量间非线性关系问题,但常用的核主成分分析是以数据服从正态分布为前提,以方差作为携带信息多少的衡量指标[7-8]。实际生产过程数据分布复杂,拟采用以信息熵为信息衡量指标的核熵成分分析作为特征提取方法,进行聚类分析。
1 信息熵
Shannon将熵的概念推广到信息理论,提出了信息熵的概念,首次对信息进行了定量描述。信息熵作为系统状态不确定性的定量评价指标,对于系统内在信息具有较强的刻画能力,其定义如下[9]:
设p(x)是数据D=x1, …, xN的概率密度函数,则该数据的信息熵可表示为
作为信息熵的发展,则瑞利熵的定义为:

信息熵是数据不确定性和事件发生的随机性的量度,从平均意义上表征数据总体信息测度的一个量,信息熵越大,信息量越多。
信息熵作为一种新的数据分析方法引起了人们广泛的关注,使用信息熵进行数据携带信息的度量,或者利用信息熵作为数据分类或聚类优劣的评价指标。核熵成分分析方法是一种将核函数学习方法与信息熵进行有机结合的优良特征提取方法。
2 核熵成分分析
核主成分分析(Kernel principal component analysis,KPCA)的核心思想是将原始数据空间投影到高维特征空间,然后对核矩阵进行特征分解,选取前k个特征值最大的特征向量作为新的数据空间,特征值其本质含义代表了数据在特征向量上的方差信息[10]。核熵成分分析(Kernel entropy component analysis, KECA)是一种新的特征提取方法,其核心思想是将原始数据投影到高维特征空间。与核主成分分析相同,同样需要对核矩阵进行特征分解,不同的是,不以特征值的大小来选择特征向量,而是选取前k个对瑞利熵贡献最大的特征向量,然后将原始数据向这些特征向量投影构成新的数据集[11]。与核主成分分析相比,是一种完全不同的成分选取方式。下面给出核熵成分分析的理论分析过程[12]:
在式(1)中,因对数函数是单调函数,所以只须考虑下式即可:

为了估计V(p),进而估计H(p),需进行Parzen窗的密度估计:

式(4)中最后一个等式由卷积理论知:高斯函数的卷积仍然为高斯函数。则符号简化后可以得到选用常用的高斯核函数K(x,x′)=作为核函数,则可以选为即为核函数,式(4)可以写为:
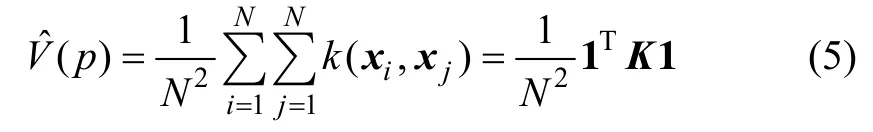
其中:N×N的核矩阵K中元素为k(xi, xj),1为每个元素均取值为1的N×1的向量。至此,瑞利熵可以表达为核矩阵的形式。瑞利熵估计还可以通过核矩阵的特征值和特征向量计算得到,核矩阵可以分解为其中Dλ为由特征值组成的对角矩阵,E为对应的特征向量e1,…,eN组成的矩阵。同时核矩阵也是特征空间中一个矩阵的内积,如果假设Φx为由对应的特征空间的数据点构成的矩阵,则可以得到因此可以改写式(5):
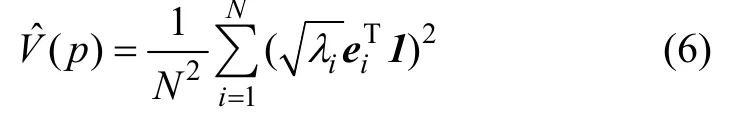

KECA分析中选择对瑞利熵估计贡献最大的前 l个特征值及其对应的特征向量,可以得到特征空间中的数据进而得到特征空间中数据点的内积在KPCA分析中,选择前k个最大的特征值及其对应的特征向量,进而可以得到特征空间的数据
经过以上的分析后给出KECA分析步骤:
(1) 给定核参数和核函数,计算核矩阵K;
(3) 由式(7)计算每个特征值所对应的瑞利熵,根据对瑞利熵贡献的大小,选择前l个特征向量和特征值;
在核熵成分分析中,发现各核熵成分间常呈现角结构,为此在角距离为相似性度量基础上利用K-mean方法进行聚类分析。
3 核熵主成分自适应聚类
在核熵成分分析中,聚类数和核参数对聚类结果具有重要影响,提出自适应选取的准则,实现核参数和聚类数的自适应选取,首先根据常用的基于欧式距离的离散度概念,引入了基于角距离[13]的离散度:
类内离散度:

其中:C为聚类数。
类间离散度:

上述类内和类间离散度为各向量间余弦值的均值,取值在0到1范围内。类内离散度表征了同类样本基于角结构距离的相似程度,类间离散度表征了不同类别样本间的相似程度。在聚类分析中,目标是使类内离散度尽可能大,类间离散度尽可能小,借鉴费希尔判别中使用类内和类间离散度的比作为准则函数[14],但基于角结构的离散度取值在0到1,被除数有可能为0或非常接近于0,这里采用基于角结构的类内和类间离散度的差作为选取的准则函数:

准则函数越大表明类内离散度与类间离散度间的差别越大,不同类别间的差别越大,相同类别的相似性越强,所以在实际应用中应尽可能使准则函数取值最大化。
在核参数和聚类数选取过程中首先需给出初始选取范围,然后使准则函数最大化选取合适的值。采用Shi等[15]提出的核参数常取值于原始数据空间各样本欧式距离中值的10%~20%作为初始范围;根据专家经验给出聚类数初始范围,若经验不足,则可使初始范围尽可能大些。
4 实验与分析
热轧带钢经过复杂的生产过程,每个生产过程均对最终的产品质量产生影响。为了进行生产过程的状态和质量分析,共收集到实际生产过程中的3种钢种的生产过程数据,包括化学元素(碳、硅、锰、磷、硫)含量,轧制过程温度信息(粗轧出口温度、精轧入口温度、精轧出口温度和卷取温度),轧制过程厚度信息(粗轧出口厚度和精轧出口成品厚度)共11个生产过程变量。3个钢种采集到的样本数分别为73,130和342。
具体的实验步骤为:(1) 利用生产过程数据构成数据矩阵(2) 取各样本欧式距离中值的10%~20%作为核参数初始范围,并根据经验给出聚类数范围;(3) 在核参数和聚类数范围内进行网格取值,分别进行KECA聚类分析,并记录每次聚类分析中计算的准则函数值;(4) 取所有准则函数值中最大值所对应的核参数和聚类数值进行KECA分析,其中核主成分数取为聚类数;(5) 利用KECA所取得的核主成分进行以cos值为相似性判据的K-mean聚类分析。
在KECA分析中核主成分数取为聚类数,原因为KECA中利用核函数实现了从原始空间到高维特征空间的映射,使非线性问题线性化,实现了在高维特征空间中每个核主成分综合提取每类样本的特征信息。如在热轧带钢钢种的聚类分析中,KECA所保留的每个核主成分表示一个钢种力学性能(屈服强度、抗拉强度、伸长率等)的综合信息。
样本空间中欧式距离的中值的 10%~20%对应的取值范围为3.8到7.6,从而选择核参数σ的初始范围为3.8~7.6。初选聚类数的范围为2~6。以核参数σ和聚类数为自变量的聚类实验准则函数取值如图 1所示。最后,选择核函数σ和聚类数分别为4.2和3.0。
实验中,K,Keca,Kpca和 cos值矩阵分别如图 2(a)~(d)所示,cos值矩阵为两两样本点之间的cos值组成的矩阵。图 2(e)给出了标准化特征值和瑞利熵结果。KECA和KPCA中选取的前3个主成分的数据分布分别如图2(f)~(g)所示。KECA可以给出明显的角结构,而KPCA没有提取出明显的角结构。

图1 带钢热轧生产过程状态聚类实验准则函数Fig.1 Criterion function in hot strip rolling experiment
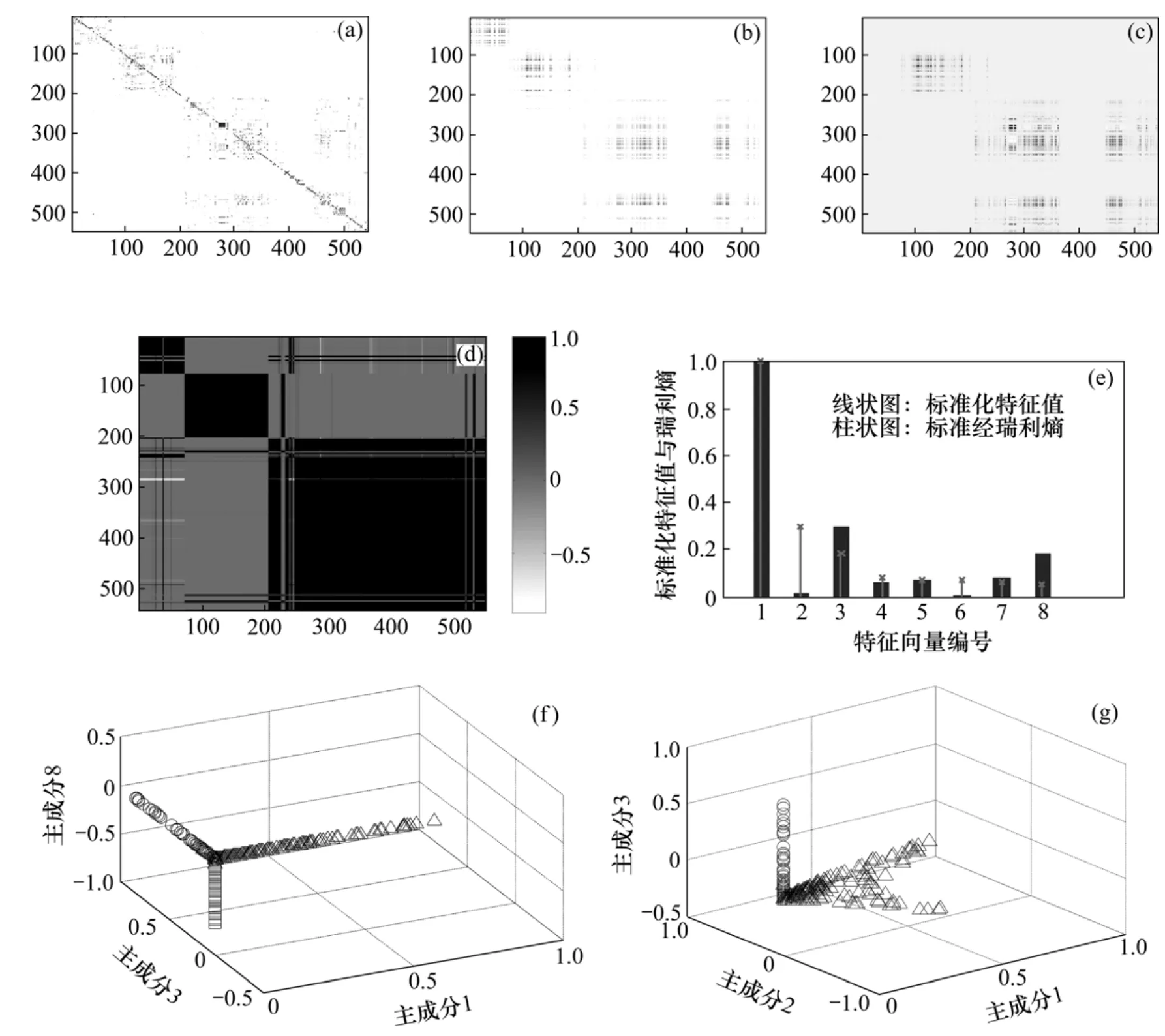
图2 带钢热轧生产过程状态聚类实验结果Fig.2 Clustering results of hot strip rolling process
利用上述的 KECA特征提取和角结构聚类分析后,表1给出了实际类别和聚类后的各类别的样本数,3种类别样本的聚类正确率分别为97.26%,99.23%和95.32%。利用KPCA分析,核参数也进行了优化选取,得到的聚类正确率分别为97.26%,88.46%和83.04%。KECA和KPCA的总体聚类准确率分别为:96.51%和86.23%,可以看到KECA具有更好的聚类结果。在带钢力学性能检测中,聚类结果不正确的样本将作为重点检测对象,这将有利于提高质量检测的针对性。
为比较KECA和KPCA的特征向量选择过程,图3给出了带钢热轧生产过程数据的前8个主成分的图。从图3中可以看到:第1,3,8主成分各有一段所对应的样本值不为零,而其他部分均基本为零,而且不为零的样本点覆盖了所有样本点。如果使用KPCA进行数据的特征提取,按照特征值的大小会选取前3个主成分。第2个主成分不为零样本与第1个主成分基本相同,均没有体现第1类样本的特征。可见KECA可以更加有效提取不同类样本的差异性,有利于不同类样本的区分。

表1 核熵成分分析带钢热轧生产聚类结果Table 1 Results of hot strip rolling clustering based on KECA个
因3类样本的聚类便于可视化表示,上述实验只采用了3类样本进行聚类分析。为了更全面了解更多钢种的聚类效果,还进行了5类样本的KECA聚类实验。5种钢种采集到的样本数分别为73,130,342,88和86,所采用的变量与前面3类相同。利用相同的方法可以获得最优的核参数4和聚类数5。
在KECA分析中,对瑞利熵值贡献最大的5个主成分分别为第2,1,8,6和17主成分。保留前5个对熵贡献最大的主成分,计算相应的角距离,得到对应的cos值矩阵如图4所示,可以看到cos值矩阵具有明显的分块特性。
而在KPCA分析中会选择特征值最大的前5个主成分,即第1~5主成分。首先给出对应特征值最大的第1,2,3主成分投影得到的数据,如图5(a)所示。由图5(a)可以看到:最大特征值对应的前3个主成分难以有效刻画数据的本质特性,难以在空间中将数据有效分离。为了形象给出2种方法的差异性,选择2种方法中差异的主成分,即给出了在第3,4,5主成分和第 8,6,17主成分投影得到的数据,分别如图5(b)~(c)所示。从图5可以看到:KECA分析中,第8,6,17主成分分别对应一类数据,具有明显的角结构特性,可以有效地提取数据的本质特性,有利于数据的聚类分析,而KPCA分析中选用的主成分不能有效表现数据的类别特征。表2给出了实际类别和KECA聚类后各类别的样本数,总体正确率为95.68%,聚类结果较为理想。而且,通过检测聚类错误样本的力学性能,发现均处于该钢种所要求的边界。在实际的生产中应尽可能避免这种情况的发生,因为其处于降级或改判为其他钢种的边缘。

图3 带钢热轧生产数据核主成分Fig.3 Kernel principal components of hot strip rolling

图4 5类热轧样本KECA分析中cos矩阵图Fig.4 Cosine matrix of hot strip rolling experiment with five class based on KECA

图5 KECA和KPCA采用的不同主成分的对比Fig.5 Comparison of KECA and KPCA principal components
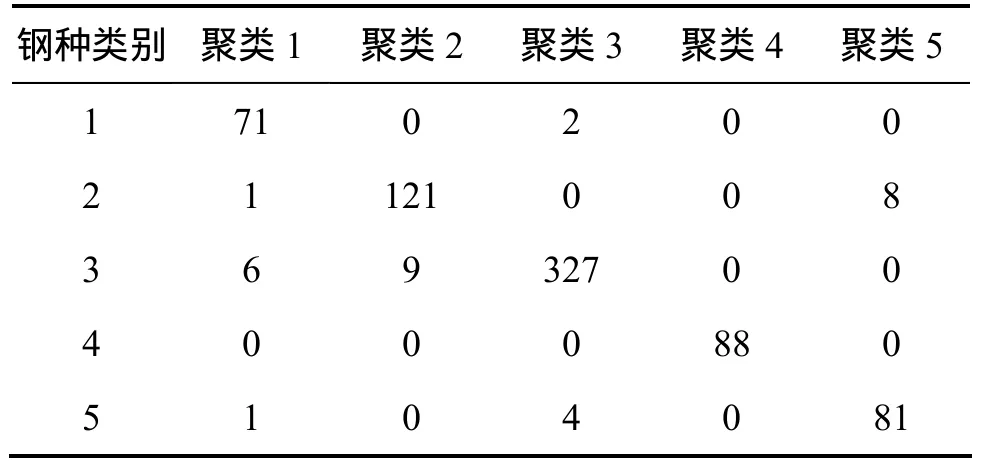
表2 核熵成分分析对5类样本带钢热轧生产聚类结果Table 2 Results of hot strip rolling clustering with five class based on KECA 个
5 结论
(1) 使用聚类方法分析热轧带钢生产工艺过程数据,间接判断热轧带钢的钢种信息,实现实时在线判断力学性能是否满足生产要求,对离群样本进行重点的离线力学性能检测,增强了控制的实时性和检测的针对性。
(2) 采用KECA提取生产数据的有效特征,并采用最大化基于角距离的类内离散度和类间离散度的差作为准则自适应选取核参数和聚类数,实现生产过程数据的自适应聚类。利用现场实际生产数据进行验证,3种带钢的聚类正确率为96.51%,与KPCA方法相比提高 10.28%。而 5种带钢的聚类正确率也达到95.68%,可以及时了解生产工艺状态。
(3) 实际的离线检测也发现聚类错误样本的力学性能均处于该钢种所规定范围的边界值,与聚类结果相吻合。在今后的研究中,努力找出导致该样本处于边界的主要工艺参数,如何调整可以改变其取值,最终达到力学性能的实时控制。
[1]孙一康. 带钢热连轧的模型与控制[M]. 北京: 冶金工业出版社, 2007: 2-13.SUN Yi-kang. Model and control for hot steel strip rolling[M].Beijing: Metallurgical Industry Press, 2007: 2-13.
[2]Kano M, Nakagawa Y. Data-based process monitoring, process control, and quality improvement: Recent developments and applications in steel industry[J]. Computers and Chemical Engineering, 2008, 32(1/2): 12-24.
[3]Braha D. Data mining for design and manufacturing: methods and applications[M]. London: Kluwer Academic Publishers,2001: 2-40.
[4]Chiang L H, Russell E L, Braatz R D. Fault detection and diagnosis in industrial systems[M]. New York: Springer-Verlag,2001: 2-10.
[5]赵凤, 焦李成, 刘汉强, 等. 半监督谱聚类特征向量选择算法[J]. 模式识别与人工智能, 2011, 21(1): 48-56.ZHAO Feng, JIAO Li-cheng, LIU Han-qiang, et al.Semi-supervised eigenvector selection for spectral clustering[J].Pattern Recognition and Application Intelligence, 2011, 21(1):48-56.
[6]Duda R O, Hart P E, Stork D G. Pattern classification[M]. 2nd ed.New York: John Wiley & Sons, 2001: 1-10.
[7]Nakagawa Y, Nakagawa S, Kano M. Quality improvement of steel products by using multivariate data analysis[C]//SICE 2007 Annual Conference. Takamatsu, Japan: IEEE, 2007: 2428-2432.
[8]Schölkopf B, Smola A, Muller K. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998,10(5): 1299-1319.
[9]Principe J C. Information theoretic learning: Renyi’s entropy and kernel perspectives[M]. New York: Springer Verlag, 2010:47-88.
[10]Jenssen R, Eltoft T. A new information theoretic analysis of sum-of-squared-error kernel clustering[J]. Neurocomputing,2008, 72(1/2/3): 23-31.
[11]Jenssen R, Eltoft T, Girolami M, et al. Kernel maximum entropy data transformation and an enhanced spectral clustering algorithm[C]//Schölkopf B, John C P, Thomas H. Proceedings of the Twentieth Annual Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2006: 633-640.
[12]Jenssen R. Kernel entropy component analysis[J]. Pattern Analysis and Machine Intelligence, 2010, 32(5): 847-860.
[13]Girolami M. Orthogonal series density estimation and the kernel eigenvalue problem[J]. Neural Computation, 2002, 14(3):669-688.
[14]Baudat G, Anouar F. Generalized discriminant analysis using a kernel approach[J]. Neural Computation, 2000, 12(10):2385-2404.
[15]Shi J, Malik J. Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000, 22(8): 888-905.

