径向热管换热器壳程数值模拟及结构参数优化

涂福炳，武荟芬，张岭，周孑民，贾煜

(1. 中南大学 能源科学与工程学院，湖南 长沙，410083；2. 长沙有色冶金设计研究院，湖南 长沙，410011)

对含硫量较高的中、低温工业烟气进行余热回收和利用，要求设备具有优良的抗低温露点腐蚀的性能,而常规的换热设备不具备该性能，且换热器寿命短，事故频繁，常造成整个生产线停产，使企业蒙受较大的经济损失[1]。同轴径向热管换热器是一种新型的高效换热器，输热能力大，均温性能优良、传热方向可逆、阻力损失小、安全耐用，较好的解决了中低温含硫烟气露点腐蚀的问题[2-3]。国内外学者目前对于热管换热器的研究主要是针对轴向热管换热器，对于同轴径向热管换热器的研究尚少。Peretz等[4-5]研究了热管换热器的几何结构对其传热性能的影响，对管间距、翅片间距以及热管的蒸发段和冷凝段长度进行优化；董其伍等[6]引入了13个参数量，建立了电站锅炉热管空气预热器的优化设计模型，并编制了组合型离散变量优化算法程序；邓斌等[7]采用各向异性多孔介质模型对管壳式换热器壳侧的流动进行了数值模拟，着重分析了管壳式换热器壳侧的湍流流动特性；黄兴华等[8-9]使用多孔介质模型对实验用管壳式热管换热器壳程单相流动和传热进行了三维数值模拟，得出了壳程流体流动和传热的分布规律；孙世梅等[10-11]运用Fluent对径向热管换热器内流体流动与传热进行了模拟研究，较好的说明了采用数值计算方法预测热管换热器传热性能的可行性；袁达忠等[12]研究了以单根热管换热为基础的热管换热器耦合源模型内的流动与传热特性，以及热管的布置方式对换热器换热的影响。另外文献[13-15]也对热管换热器进行了研究。在此，本文作者将对同轴径向热管换热器进行数值模拟研究。

1 数值模拟

1.1 物理模型

热管换热器内部几何结构复杂，同时考虑到换热管内部冷却介质对换热的影响，和烟气与管外壁、管内壁与冷却水的流固耦合传热传质，以及高温烟气对外管的物理化学侵蚀、物性变化等因素。假定换热器在稳定工况下运行，各操作参数恒定，没有波动变化，换热器内部热管运行状态良好。

换热器具有壳程大、管内径小、管子数目多，尤其是在圆管的划分上，很容易出现扭曲度较大的网格，这需要不断的调整网格的大小，难度非常大。本文依靠点、线、面、体的步骤，将整个计算区域划分为几个不同区域分块划分网格，热管直管段、弯头段、冷却水进口、出口、换热器两侧挡板、换热器喇叭口段等。采用六面体结构网格划分整个计算区域。采用Gambit 2.2 进行网格划分。热管换热器的几何参数如表1所示，建立的热管换热器的三维计算区域网格如图1所示。

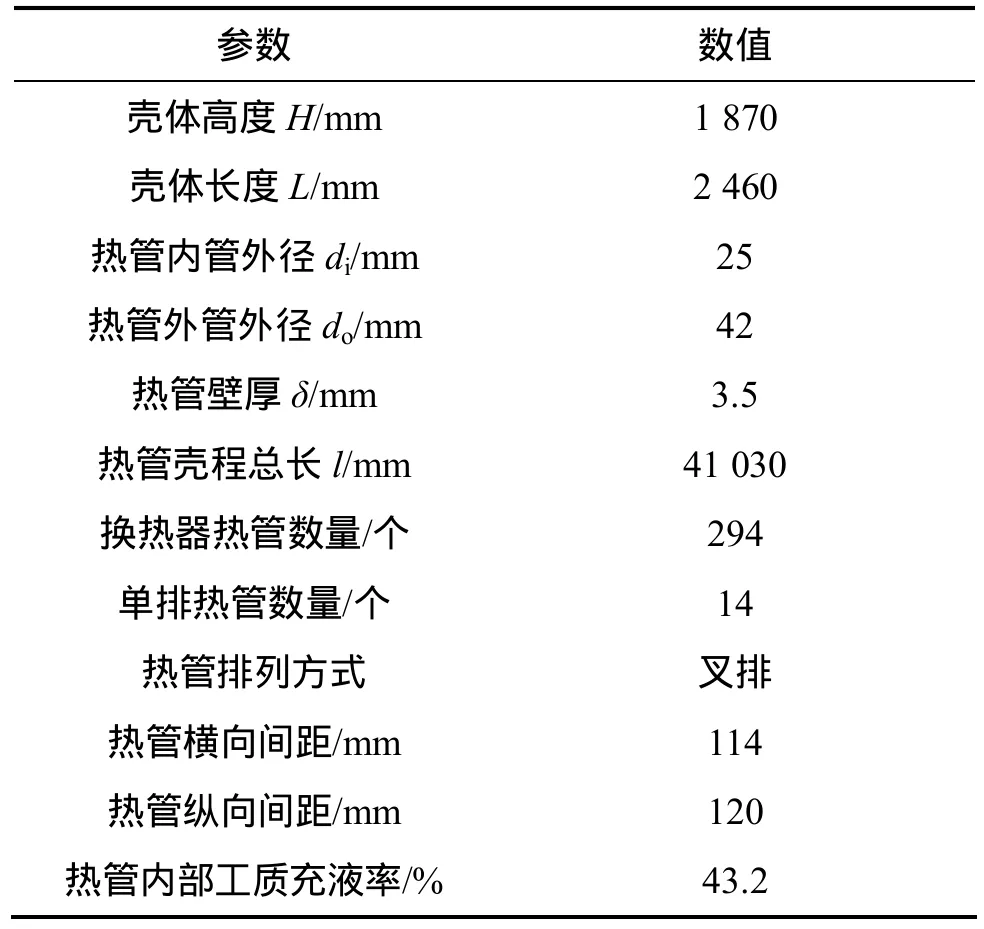
表1 同轴径向热管换热器的几何参数Table 1 Structural parameters of radial heat pipe heat exchanger

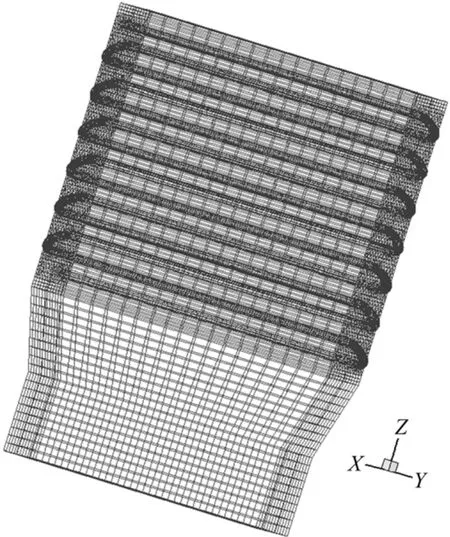
图1 同轴径向热管换热器的三维网格图Fig.1 Three-dimensional grid of radial heat pipe heat exchanger

1.2 数学模型

热管换热器内的气体流动一般为湍流流动，假设热管换热器内的流动为不可压缩湍流运动，经过雷诺时均化的控制方程可表示为如下形式：

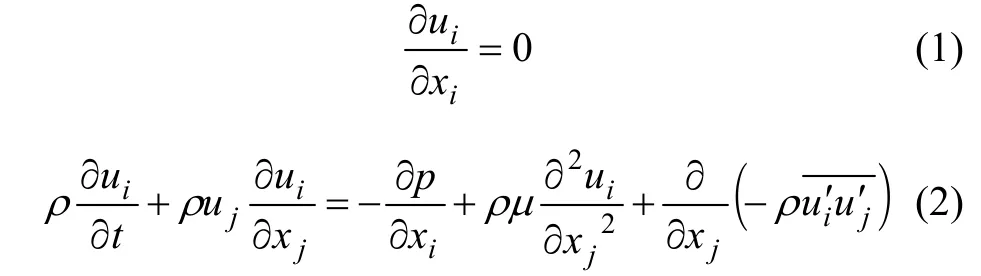
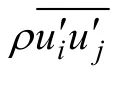
控制方程确定后，要对流场控制方程进行离散,本文采用精度较高的 QUICK格式来离散对流项；对动量方程的离散通过修正压力梯度项来控制；由于热管换热器内流动的旋转特性，压力插补格式采用PRESTO格式；同时考虑到热管换热器内流动的复杂性，采用SIMPLE算法进行求解。

1.3 耦合传热问题数值计算

数值解法可分为分区求解边界耦合和整场求解两种方法。换热器的烟气与热管的流固耦合问题用整场求解的方法最为有效。外流域烟气和热管外表面，同时冷却水流域和热管内表面，产生耦合交界面。界面处处理方法采用调和平均法。固体和气体控制容积节点P和E的导热系数λ不相等，则由界面上的热流密度连续的原则，由 Fourior定律，可得界面上的当量导热系数的调和平均公式：

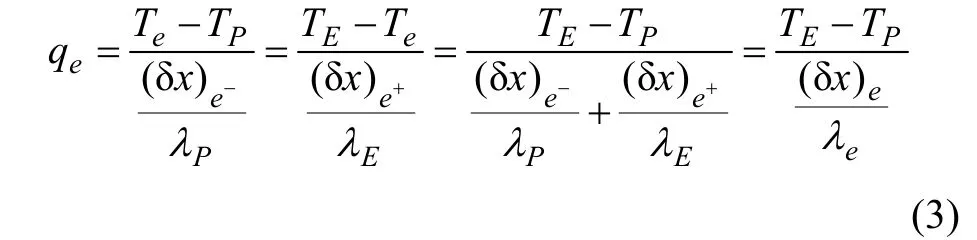
式中：qe为界面e上的热流密度，W/m2；T为热力学温度，K；(δx)e为P和E节点的距离； (δx)e-为节点P到截面e的距离； (δx)e+为节点E到截面e的距离；λ为导热系数，W/(m2·K)。

由式(3)可得：

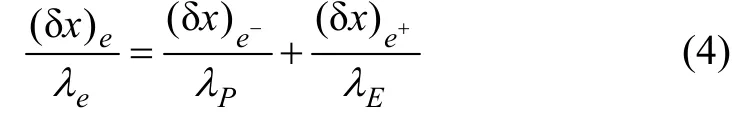
温度场耦合求解时，固体与流体的分界面自然地成为控制容积的界面，该界面上的当量扩散系数应该采用上面介绍的调和平均的方法。固体与流体区中的导热系数采取各自的实际值，但在固体区中的比热容则采用流体区的比热容之值，这样才能保证耦合界面上的热流密度连续。

1.4 模型设置求解及边界条件

使用分离式求解器，非稳态隐式格式求解；速度压力耦合方式采用基于交错网格的SIMPLE方式；流体为烟气，物性参数由热态试验中测试而得；假设入口来流的速度均匀稳定，壳体壁面采用不可渗透无滑移绝热边界。

入口采用速度入口边界条件，烟气具体参数见表2，冷却水入口给定流速和水温，入口湍流采用湍流强度和水力直径。出口采用压力出口边界条件。壁面为无滑移边界条件，近壁区的处理采用壁面函数法。进行传热模拟需要选定能量方程，对换热管束壁面和翅片，设定为无滑移，无渗透，并选择Coupled流固耦合条件，将两侧烟气和水流耦合起来。壁面设置厚度为 8 mm，导热系数设置为充液率 43.2%的热管等效导热系数值，可由下式得出：

式中：λeff为等效导热系数；R为充液率。

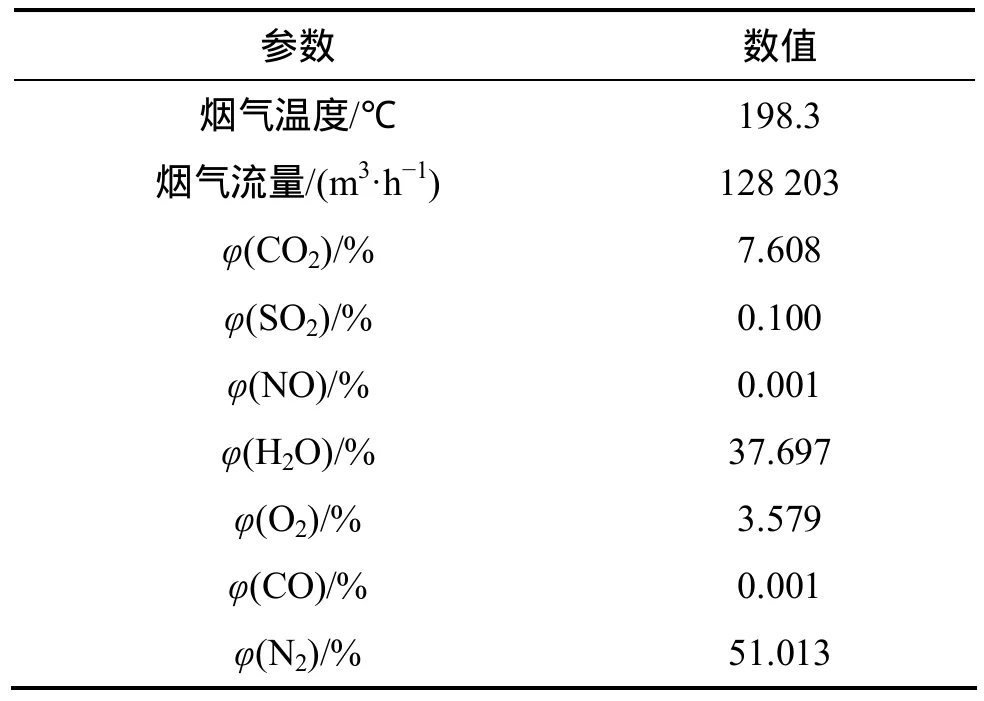
表2 烟气参数表Table 2 Parameter list of smoke

2 数值仿真结果验证与误差分析

2.1 仿真结果分析

图2所示为不同切面上换热器第1～14排等温线。由图2可知：对于换热器壳程，越是靠近热管管壁的地方，等温线越是密集，证明温度梯度越大。在热管两侧的边缘处的烟气温度高于管束尾部的烟气温度。这是由于在高雷诺数下，管间容积内的流体变成具有高湍流度的旋涡流。在热管迎风面的尾部，流体中的压力增大，沿流动方向的速度下降，因为在边界层内流体微团由于摩擦而失去能量，动能不足以克服增长的压力，于是微团的运动逐渐减慢，以致停下来向相反的方向运动，逆向的微团互相推挤，造成热管尾部湍流度增加，换热增强，所以尾迹区内的温度比同一位置上的壳程上的温度要低些。

图2 不同切面上换热器第1～14排等温线(单位：K)Fig.2 Isotherms of different cross sections in heat exchanger range from row 1 to 14

图3 换热器内热管局部速度矢量和流线图Fig.3 Local velocity vector and flow pattern of heat pipe in heat exchanger

图 3所示为换热器内热管局部速度矢量和流线图。由图3可以看到：在烟气流经管束时，在管束尾部形成一个楔形的涡流区，涡流区的速度明显低于其同Z坐标的其他区域，在热管的X向侧缘，流体速度达到最大，最大流速均大于烟气入口流速。对第一排和其后深层各排管的绕流状况进行对比，可以发现，深层管排迎面的来流具有更高的湍流度，与第一排相比，其脱体点的位置向流动的下游方向移动。其楔形区的流束较窄，而且返回流束具有更为复杂的流线图形。图中在绕流尾迹区形成的一对旋转方向相反的对称漩涡，称为卡门涡街。当壳程流体出现卡门涡街时，由于在管子两侧交替地释放漩涡，其绕流情况是不一样的，流动阻力也不同，而且有周期变化。卡门涡街作用力方向的交变性是由于在管子尾迹流的卡门涡街中，两列旋转方向相反的漩涡周期性均匀交替脱落引起的。当涡街作用力的交变频率与设备管束弹性结构的固有频率相耦合发生共振时，造成了换热器的振动问题。

图4所示为换热器X=110 mm，Y=1 230 mm，壳程Z向湍流强度。由图4可以看出：湍流强度在涡流中心区域最大，且中心区域的换热强度要明显高于边缘处。随着流动深度的增加，换热器内部的湍流强度越来越大，当烟气离开热管区域时，湍流强度明显减小。

2.2 仿真结果验证

仿真结果与现场测试数据对比见表 3。4个测点分布于热管换热器的中心，在Z向上变化，其中测点4的位置，位于最后一排热管的下方120 mm处。由表3可知：误差在10%范围内，证明用数值模拟方法是可行的。造成误差的原因是多方面的，主要包括数值仿真计算中的误差和测试中的误差两方面。

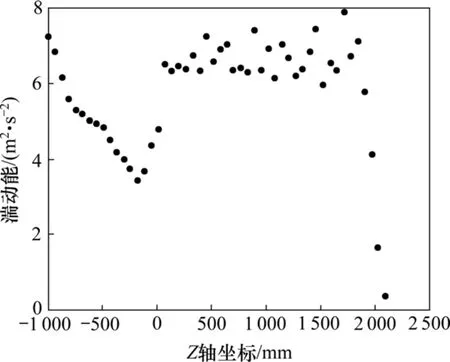
图4 换热器X=110 mm，Y=1 230 mm，壳程Z向湍流强度Fig.4 Turbulivity in shell side along Z-axis (X=110 mm,Y=1 230 mm)

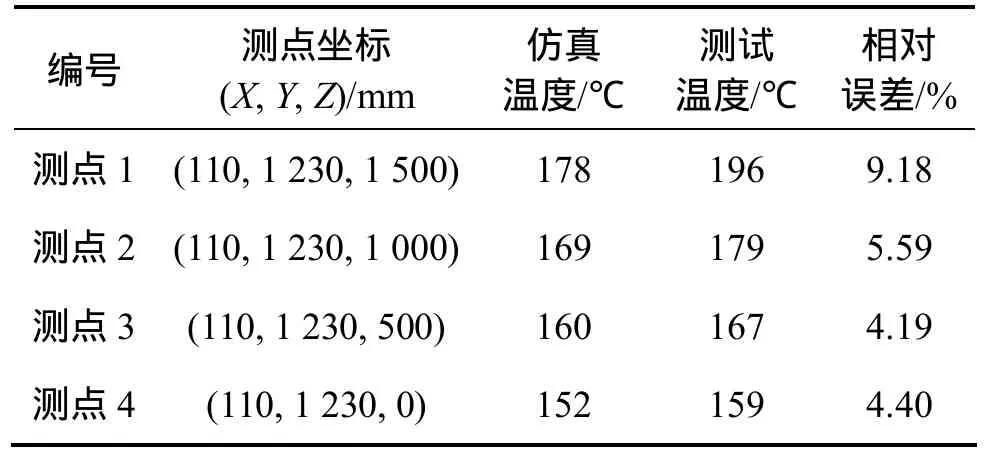
表3 仿真值与测试值比较Table 3 Comparison of simulation results and test results

3 热管换热器结构参数优化

为了进一步提高换热器的技术性能，在现有模型的基础上对换热器的结构参数进行优化研究。由于翅片数目庞大，布置密集，要想实现整台换热器的实体模拟困难很大，根据换热器管排和翅片布置的对称性，在建模时应用对称边界条件，选取一个代表性单元作为计算区域，使得实体模拟得以实现。结构参数优化选用的模型如图5所示，具体参数见表1，选取面1-1，2-2和面3-3，4-4所包围的区域为计算区域，局部网格放大图如图6所示。在模拟计算时，保持冷却水入口流量和温度稳定，分别研究热管管距、管外翅片高度、翅片间距的变化对换热器单位压降换热系数α/ Δp 的影响规律。

3.1 热管横向管距

横向管距变化下热管出口烟温与出口水温变化规律如图7所示。由计算结果可知：烟气出口的平均温度和冷却水出口温度都随横向间距的增加而变大。其中冷却水出口温度增加是由于进口烟气流速保持不变的情况下，随着横向间距的增大，进口烟气流量增大，换热量增大所致。

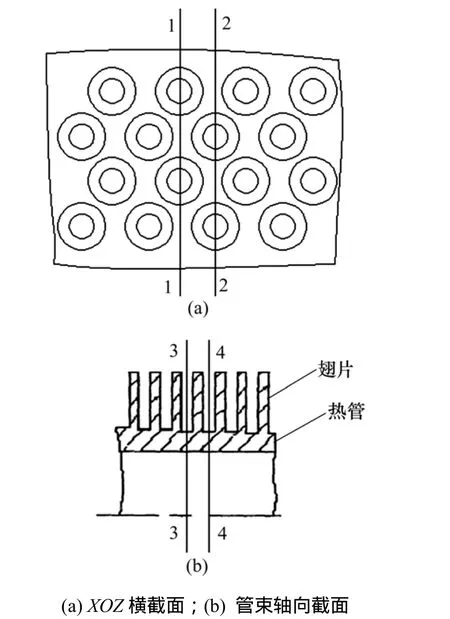
图5 换热器计算区域示意图Fig.5 Schematic diagram of heat exchanger computational domain

图6 同轴径向热管换热器的局部三维网格图Fig.6 Local three-dimensional mesh of radial heat pipe heat exchanger

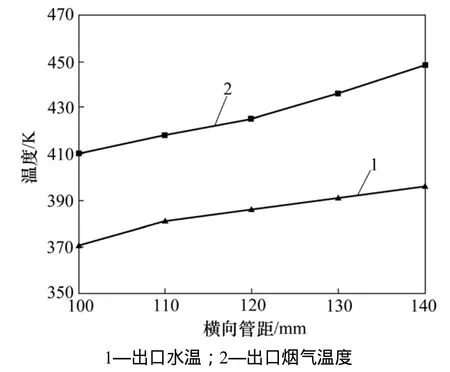
图7 横向管距变化下热管出口烟温与出口水温变化规律Fig.7 Export smoke and water temperature under different transverse spaces of heat pipe

由图7可以看出：保持纵向间距120 mm不变，横向间距在105～120 mm之间时，两者温压最小，换热器效率在此处较大；在压降方面，换热器压降随着热管横向间距增加，压降呈线性减小，且降幅明显，热管横向间距由102 mm增加到114 mm，压降平均可减小105 Pa，降幅明显。因此，横向间距对换热器阻力影响显著。

以换热器的单位压降换热系数α/Δp为优化目标。图8所示为横向管距变化下单位压降换热系数。由图8可知：在横向间距120 mm处，单位压降换热系数达到最大值，换热器性能最优。根据换热器的设计计算公式，横向管距 ST=1.02～1.5df，df为翅片外直径，本文所用换热器df为96 mm，横向管距的范围为98～144 mm。综上所述，换热器横向管距的最优值在114～120 mm 之间。

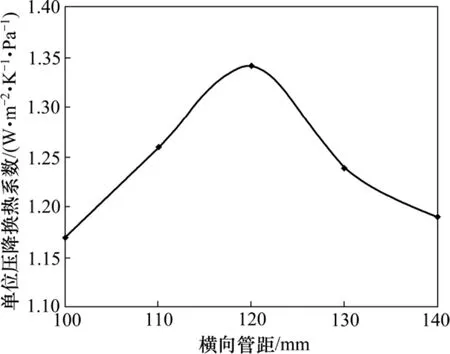
图8 横向管距变化下单位压降换热系数Fig.8 Heat transfer coefficient of unit pressure drop under different transverse spaces of heat pipe

3.2 热管纵向管距

热管换热器热管布置设计时，在主流方向，热管应该选择适当的间距；随着纵向间距的增大，热管的排列方式越接近于顺排。在叉排管束中，阻力随纵向管距的增加而减小，因为赖以形成漩涡的管间容积大小主要取决于纵向管距。当纵向管距减小到很小时，它对流通截面的影响更大。

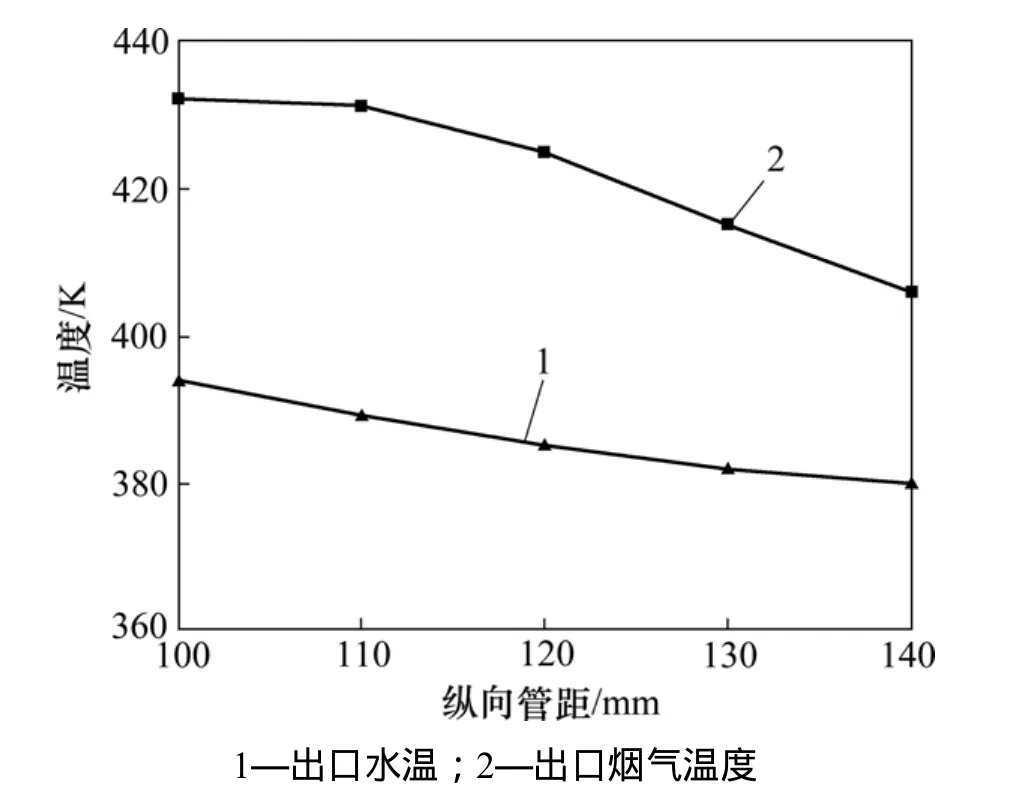
图9 纵向管距变化时，热管出口烟温与出口水温变化规律Fig.9 Export smoke and water temperature under different longitudinal spaces of heat pipe

图9所示为纵向管距变化时，热管出口烟温与出口水温变化规律。可见：换热器管排总数不变时，纵向管距越大，烟气在换热器中停留的时间越长，换热量增大。以单位压降换热系数为优化目标，纵向管距越大，壳程内部流动越接近于管子的顺排，压降减小，所以单位压降换热系数增大，但是纵向管距增大，同时也减小了流动的湍流强度，壳程换热系数降低，对设备的紧凑性同样有较大的影响。图 10所示为纵向管距变化下换热器单位压降换热系数。由图10可得出最佳的纵向管距在120～125 mm之间。

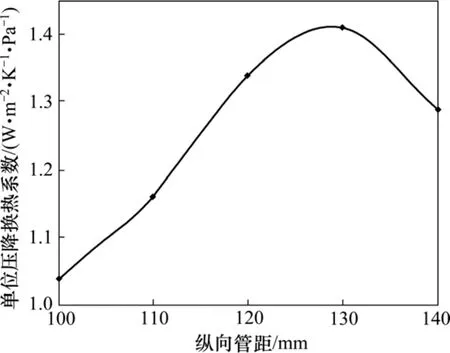
图10 纵向管距变化下换热器单位压降换热系数Fig.10 Heat transfer coefficient of unit pressure drop under different longitudinal spaces of heat pipe

3.3 翅片高度

用翅片扩大换热管表面积和促进介质的紊流，从而提高传热效率。在选择翅片高度时，除了追求效率高之外，还应尽可能与翅片厚度相匹配。图 11所示为翅片高度变化下局部对流换热系数变化规律。由图11可知：翅片的高度越小，翅片管表面附近的流动状况也就越接近与无翅片管的状况，随着翅片高度的增加，翅片间的流动越具有明显的间隙流动特征。翅片高度在 25 mm时，局部对流换热系数达到最大，之后翅片高度增加对换热的影响并不明显，若考虑到换热器压降性能，此时，热管换热器翅片高度不应高于26.5 mm。

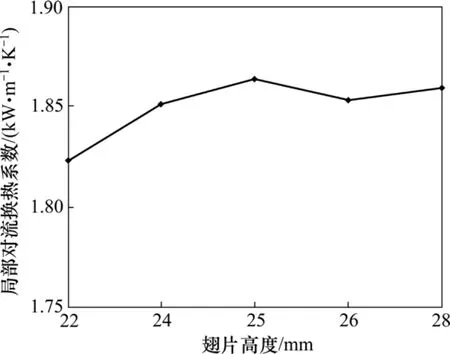
图11 翅片高度变化下局部对流换热系数变化规律Fig.11 Local convection heat transfer coefficient under different fin heights

3.4 翅片间距

烟气的具体流体力学状况，决定了外侧肋化表面的换热强度。了解翅片管周围流体的流动，才能对翅片局部换热系数的变化做出充分的解释。由计算结果可知，当翅片间距由8 mm到4 mm，随着翅片间距减小，换热面积增大，换热效果增强。图 12所示为不同雷诺数和翅片间距下局部对流换热系数变化规律。从图12中可以看出：翅片间距在6 mm(两翅片表面之间的距离为5 mm)以内时，换热随翅片间距的加大而明显增强，但继续加大时翅片间距时，换热效果增强不明显。这是翅片间距的增大，换热面积减小的结果；随着 Re的增大，翅片间距对换热的影响逐渐减弱。这是由于 Re的增大，使边界层厚度变小，在较小的翅片间距值之下，换热系数即达到峰值。综上所述，翅片间距为6 mm时，换热效果较为理想。

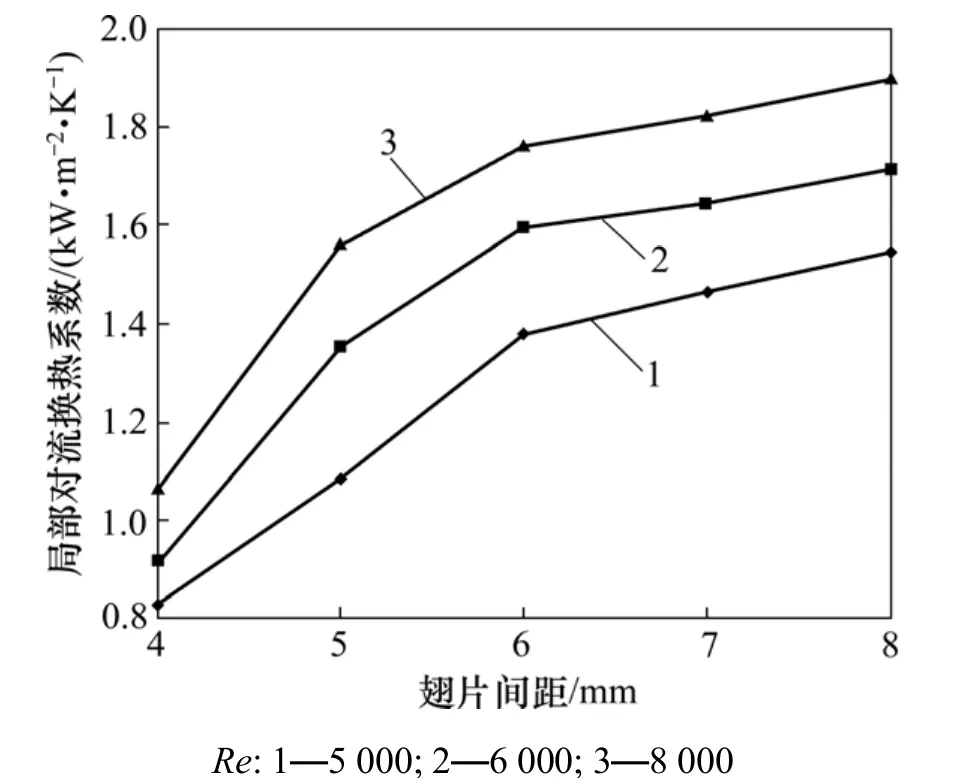
图12 不同雷诺数和翅片间距下局部对流换热系数变化规律Fig.12 Local convection heat transfer coefficient under different Re and fin spaces

4 结论

(1) 换热器壳程中烟气离热管壁面越近，温度梯度越大。在热管两侧边缘处的烟气温度高于管束尾部的烟气温度。这是因为在边界层内流体微团互相推挤，造成热管尾部湍流度增加，换热增强。

(2) 烟气流经换热器壳程时，在管束尾部形成一个楔形的涡流区，速度在流体出现脱体的地方达到最大值。湍流强度在中心区域也是最大，因此，中心区域的换热强度明显高于边缘处。

(3) 换热器结构参数优化结果是：横向管距为114～120 mm；纵向管距为120～125 mm；翅片高度不应高于26.5 mm；翅片间距为6 mm。

[1] 庄骏, 张红. 热管技术及其工程应用[M]. 北京: 化学工业出版社, 2000: 33-38.ZHUANG Jun, ZHANG Hong. Technology and engineering applications of heat pipe[M]. Beijing: Chemical Industry Press,2000: 33-38.

[2] Vafai K,Wanga W. Analysis of flow and heat transfer characteristics of an asymmetrical flat plate heat pipe[J]. Int J Heat Mass Transfer, 1992, 35(9): 2087-2099.

[3] Wang Y, Vafai K. An experimental investigation of the thermal performance of an asymmertrical flat plate heat pipe[J]. Int J Heat Mass Transfer, 2000, 43(15): 2657-2668.

[4] Peretz R, Bendescu J. The influence of the heat pipe heat exchanger's geometry on its heat transfer effectiveness[J].Journal of Heat Recovery Systems, 1983, 3(1): 23-34.

[5] Peretz R, Horbaniuc B. Optimal heat pipe heat exchanger design[J]. Journal of Heat Recovery Systems, 1984, 4(1): 9-24.

[6] 董其伍, 王丹, 刘敏珊. 余热回收用热管及热管式换热器的研究[J]. 工业加热, 2007, 36(4): 37-40.DONG Qi-wu, WANG Dan, LIU Min-shan. Research on heat pipe and heat Pipe heat exchanger for waste heat recovery[J].Industrial Heating, 2007, 36(4): 37-40.

[7] 邓斌, 陶文铨. 管壳式换热器壳侧湍流流动的数值模拟及实验研究[J]. 西安交通大学学报: 自然科学版, 2003, 37(9):889-893.DENG Bing, TAO Wen-quan. Numerical simulation and experimental study on turbulent flow in shell side of shell-and-tube heat exchangers[J]. Journal of Xi'an Jiaotong University: Natural Science, 2003, 37(9): 889-893.

[8] 黄兴华, 王启杰, 陆震. 管壳式换热器壳程流动和传热的三维数值模拟[J]. 化工学报, 2000, 51(3): 297-302.HUANG Xing-hua, WANG Qi-jie, LU Zhen. Three dimensional numerical simulation of fluid flow and heat thransfer in shell-and-tube heat exchanger[J]. Journal of Chemical Industry and Engineering (China), 2000, 51(3): 297-302.

[9] 黄兴华, 陆震, 刘冬暖. 换热器壳侧紊流流动特性的数值研究[J]. 上海交通大学学报: 自然科学版, 2000, 34(9):1191-1194.HUANG Xing-hua, LU Zhen, LIU Dong-nuan. Numerical study of turbulent flow characteristics in shell side of shell-and-tube heat exchangers[J]. Journal of Shanghai Jiaotong University:Natural Science, 2000, 34(9): 1191-1194.

[10] 孙世梅, 张红. 热管换热器流动与传热的 CFD模拟及试验研究[J]. 南京工业大学学报: 自然科学版, 2004, 26(2): 62-66.SUN Shi-mei, ZHANG Hong. Analysis of CFD simulation with experiment of heat transfer and pressure drop for heat pipe heat exchanger[J]. Journal of Nanjing University of Technology:Natural Science, 2004, 26(2): 62-66.

[11] 孙世梅, 张红. 热管换热器传热性能及温度场数值模拟研究[J]. 化工学报, 2004, 55(3): 472-475.SUN Shi-mei, ZHANG Hong. Numerical simulation of thermal performance and temperature field in heat exchanger[J]. Journal of Chemical Industry and Engineering (China), 2004, 55(3):472-475.

[12] 袁达忠. 热管换热器的两相流模型与耦合传热的研究[D]. 大连: 大连理工大学化工学院, 2008: 62-102.YUAN Da-zhong. Two phase flow model and conjugate heat transfer for heat pipe heat exchanger[D]. Dalian: Dalian University of Technology. School of Chemical Engineering,2008: 62-102.

[13] 陈丹. 高温热管换热器的模拟优化研究[D]. 南京: 南京工业大学机械与动力工程学院, 2002: 30-35.CHEN Dan. Research on simulation and optimization of high temperature heat pipe heat exchanger[D]. Nanjing: Nanjing University of Technology. School of Mechanical and Power Engineering, 2002: 30-35.

[14] 赵安林. R600a在重力热管散热器中的工作实验研究[D]. 重庆: 重庆大学动力工程学院, 2002: 13-19.ZHAO An-lin. Experimental investigation of thermalsiphon radiator for refrigerant R600a[D]. Chongqing: Chongqing University. School of Power Engineering, 2002: 13-19.

[15] 郭雪华. 热管式真空蒸发器的设计和试验研究[D]. 大连: 大连理工大学化工学院, 2000: 30-32.GUO Xue-hua. The design and experimental studies on heat pipe vacuum evaporator[D]. Dalian: Dalian University of Technology.School of Chemical Engineering, 2000: 30-32.