混凝土结构地震需求参数敏感性分析

尹犟，胡其高，李鹏

(1. 中南林业科技大学 土木工程与力学学院，湖南 长沙，410004；2. 国防科技大学 指挥军官基础教育学院，湖南 长沙，410072；3. 湖南省建筑设计院，湖南 长沙，410011)

近年来，一些研究者从地震灾害造成的损失出发，对一些抗震工程领域主要的不确定因素进行了敏感性分析[1-3]，其中：Porter等[1]分析了建筑物的地震损失估计值对于场地运动强度、结构特性、构件易损性和单修复造价等不确定性因素的敏感性；Bake等[2]基于一次二阶矩(FOSM)方法，建议了估计结构震后修复总造价的实施步骤；Aslani等[3]以构件为基础，采用可靠度方法对建筑在地震作用下的年预期损失值进行了估计。这些研究人员均未直接对结构的地震需求参数(Earthquake demand parameters，EDP)进行研究。实际上，EDP可以更加直观地体现结构的抗震性能。在此，本文作者综合运用3种敏感性分析法(一次二阶矩法、龙卷风图形法和数理统计方法)，以1个典型混凝土框架结构为例，选择4种对其抗震性能产生关键影响的EDP(含基底剪力需求、楼层加速度需求、顶点位移需求、层间位移比需求)进行敏感性分析。根据分析结果，对一系列基本不确定因素进行重要性排序，从中选择对EDP不确定性产生重要影响的敏感性因素。

1 敏感性分析的方法

1.1 一次二阶矩(FOSM)法

一次二阶矩(FOSM)方法在结构可靠度理论中具有重要地位，是国际标准《结构可靠性总原则》(ISO 2394)[4]以及我国《建筑结构可靠度设计统一标准》(GB 50068—2001)[5]中推荐采用的方法。本文运用该方法进行敏感性分析。其理论如下。

设随机变量Y和随机矢量X=[ X1, X2, …, Xn]T之间有函数关系：Y=g(X)；将Y在X的均值μX处按Taylor级数展开可得：

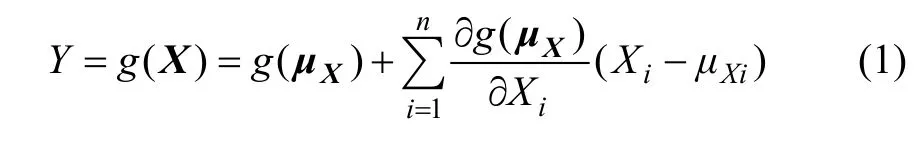
式中：μX为随机矢量 X 的均值矩阵，μ=[x ,x,…,x]T； ∂g (μ )/∂X为函数 g(·)关于随X12nXi机变量Xi的偏导数矩阵在其均值μX处的值。根据述(1)及可靠度基本理论，随机变量Y的均值μY(一阶矩)为：

同理，随机变量Y的方差2Yσ(二阶矩)为：

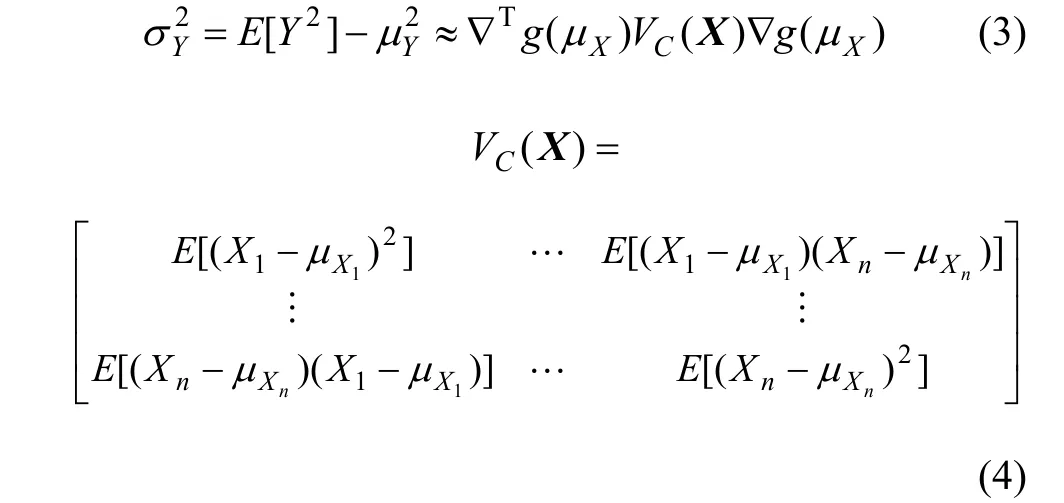
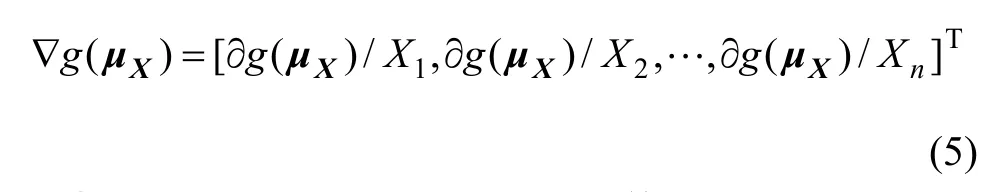
式中：VC(X)为随机矢量X的协方差矩阵；▽ g ( μX)为函数g(·)关于矢量X的梯度矩阵在其均值μX处的值。

对敏感性进行分析时，由于式(3)能够反映输入参数X的不确定性通过函数g(·)进行传递，从而导致输出结果Y也出现不确定性(σY)的过程，该式尤为重要。在敏感性分析中往往将σY作为反映Y对于X的敏感度的参量[6]，若σY很大，则表明Y对X很敏感；反之，则表明Y对X不敏感。

从理论上讲，由式(3)计算的σY体现了随机矢量X对于输出结果Y的综合影响，可直接应用于敏感性分析。但在实际应用中，往往希望能够分别确定EDP对每一个随机变量Xi的敏感度，从而通过排序识别出主要的敏感性因素。此时，可将除随机矢量中除 Xi以外的其他随机变量全部设置为其均值，并将输出变量Y重新表示为：

将上式按Taylor级数展开，并经过类似式(2)和(3)的推导可得：

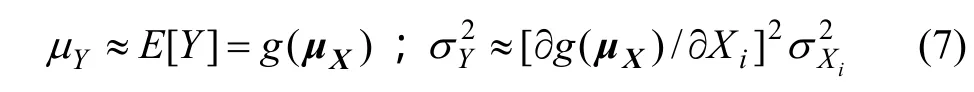
式中：μY和σY分别为则随机变量Y的均值和标准差。

显然，尽管式(3)和式(7)均可用于敏感性分析，但它们的特点各不相同。式(3)能够考虑各随机变量之间的相关性，而式(7)则可分别计算输出参数对于每一个随机输入变量的敏感性。

本文运用有限元方法得到输入、输出参数间的函数关系 g(·)，而 g(·)关于随机变量的 Xi的梯度采用有限差分法确定，即：

式中：ΔXi为第 i个输入随机变量 Xi的扰动量，本文将其取为标准差 σXi的某个分位数，即： ΔXi=cpσXi(其中，cp为扰动系数，可通过收敛性试验确定)。

1.2 Tornado图形法

Tornado图形法最早应用于决策分析领域。近年来，一些研究者利用该方法对建筑物的地震损失进行了敏感性分析[1]。Tornado图形由一系列被称为“幅摆”的水平横杠组成，每一条“幅摆”对应于1个随机变量，其宽度体现了输出结果的变异性，见图 1(a)。若某个输入变量对输出结果的变异性产生了显著影响，则其“幅摆”也就较宽，反之则较窄。在确定了各输入变量对应的“幅摆”宽度后，可按照由宽至窄的顺序对其重要性进行排列(见图 1(b))。排序后的图形与龙卷风形态相似，该方法为Tornado(龙卷风)图形法。本文利用Tornado图形法进行敏感性分析的具体步骤如下。

(1) 首先根据需要确定EDP的类型，如基底剪力需求、顶点位移需求等。

(2) 任选1个随机输入变量X，根据其概率分布的上、下界(如10%和90%)确定与之相应的输入变量下限值XLB和上限值XUB，见图1(a)。

(3) 将除X以外的其他随机变量全部设置为其均值，并将XLB和XUB分别输入结构模型进行有限元分析，从而得到EDP的下限值XLB和上限值XUB，见图1(a)。

(4) 取|XUB-XLB|为 X对应的“幅摆”宽度，并将其表示在初始图形中，见图1(b)。

(5) 重复上述步骤直至获得所有输入变量对应的“幅摆”宽度为止，并将其自上而下按降序重新排序。排序后的图形即为Tornado图，图中的“幅摆”宽度反映了EDP对所选随机输入变量的敏感性，见图1(b)。

1.3 数理统计方法

为了提高分析效率，本文采用FOSM法及Tornado图形法进行敏感性分析，但涉及场地运动的具体特征时(即指地面运动记录中除强度以外的其他特性[6])，上述方法则不再适用。这是由于场地运动具体特征PGM极为复杂，其不确定性很难用简单的概率函数描述。

本文从美国太平洋地震工程研究中心PEER强震数据库中选择53条实测地面运动加速度记录，并将其缩放至相同的峰值地面运动加速度 PGA，以模拟PGM(地面运动加速度记录的具体特征)的不确定性。所有地面运动记录均取自断层距大于10 km的场地，其地下30 m平均剪切波速250≤vS30≤550 m/s，场地特征周期0.35≤Tg≤0.45 s，基本与我国规范定义的Ⅱ类场地等效，见表1。其中，地震动特征周期值Tg根据Vidic等[7]提出的公式计算，即：

式中：PGA和 PGV分别为地面运动加速度和速度的峰值；ca为谱加速度与峰值加速度的比值；cv为谱速度与峰值速度的比值。根据Vidic等[7]的研究成果，系数ca和cv可分别取为2.5和2.0。

2 混凝土框架结构的敏感性分析

以1榀位于8度设防(0.3g)、Ⅱ类场地(第2组)的典型钢筋混凝土框架结构为例，对影响其抗震性能的4种EDP敏感性进行分析。该框架共3跨7层，单跨跨度为6 m；底层层高为4.2 m，其他层层高为3.6 m。梁、柱混凝土为C30级，纵筋为HRB335级，箍筋为HRB235级。表2所示为该框架的配筋参数设计值，列出了按受荷范围集中到框架梁、柱上的荷载标准值，其中：括号内数值为活荷载标准值，其他为恒荷载标准值；梁上荷载为等效均布荷载，单位为kN/m；柱上荷载为集中荷载，单位为kN。表3所示为7层平面框架梁、柱尺寸及配筋。所选地面运动加速度记录见表1。

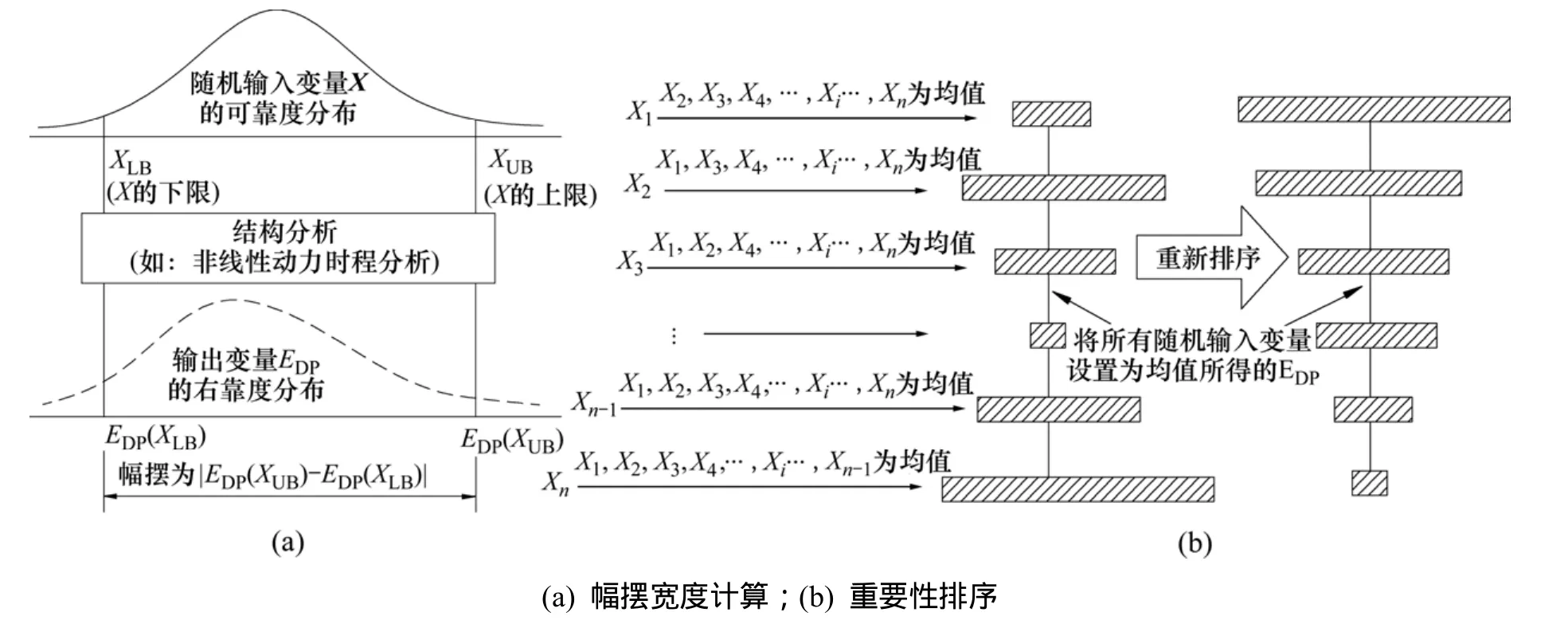
图1 Tornado图形制作方法Fig.1 Fracture of Tornado diagrams

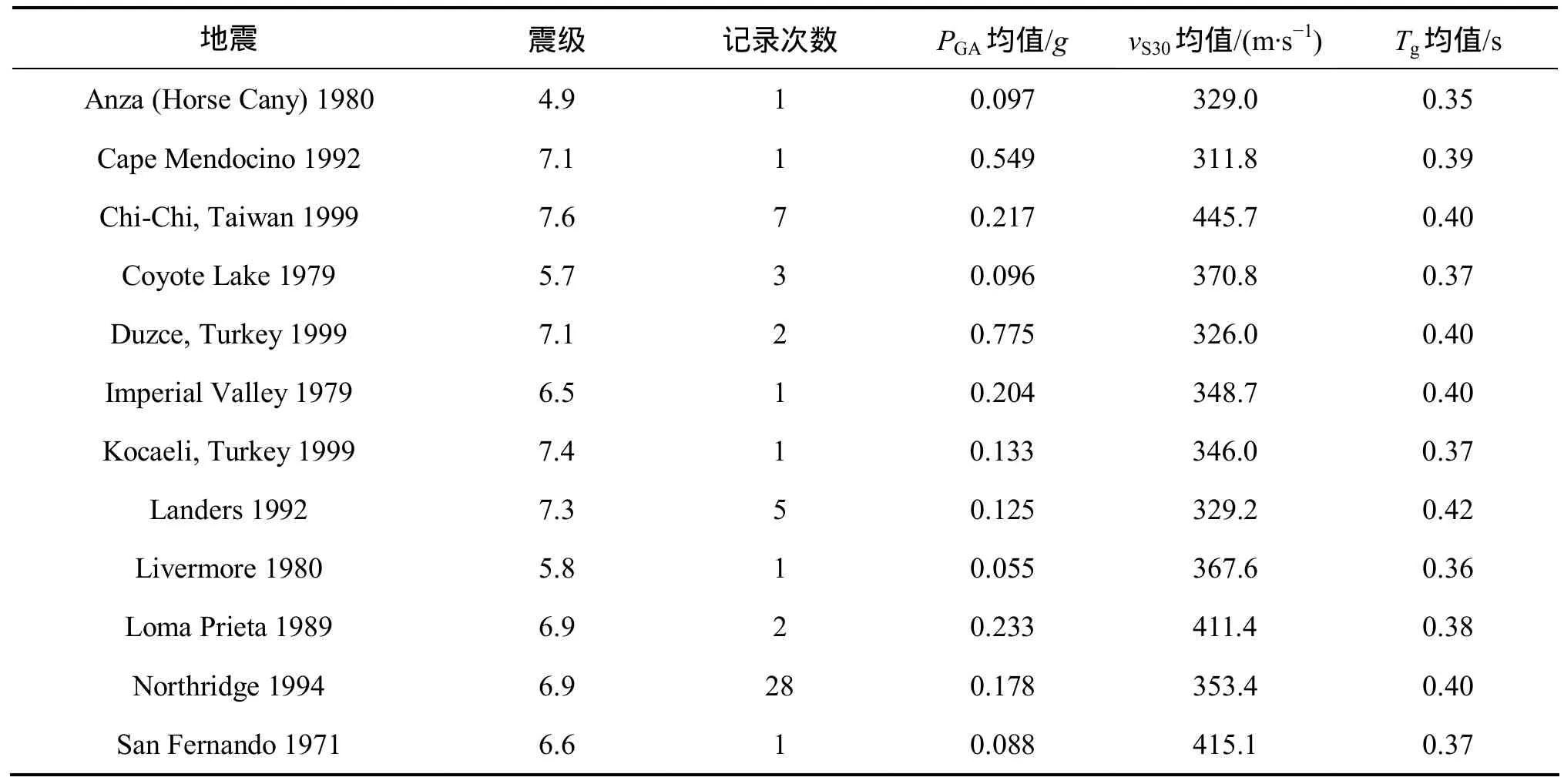
表1 地面运动加速度记录[19]Table 1 Acceleration records of ground motions[19]

表2 不确定性因素的概率分布类型及统计参数Table 2 Probabilistic distribution and statistic parameters of uncertainties

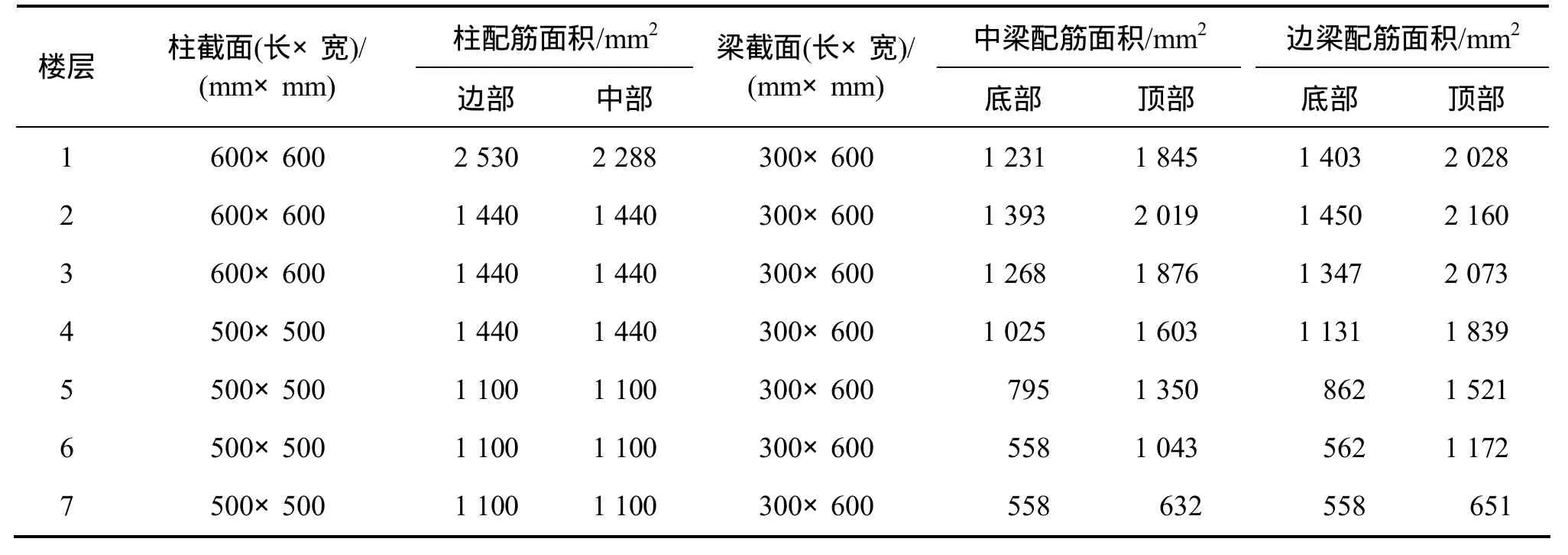
表3 7层平面框架梁、柱尺寸及配筋Table 3 Reinforcing bars and dimensions of 7-story planar frame

2.1 基本的不确定性因素

在抗震工程领域，基本的不确定性因素主要来源于场地运动和结构特性这2个方面。鉴于上述2个方面的不确定性因素较多，进行全面分析尚有困难，表2所示仅列举一些主要不确定性因素，并参照国内、外相关研究成果对其概率特征和统计参数进行归纳。

2.2 结构模型及计算方法

采用通用有限元设计分析软件 SAP2000建立计算模型，模型中根据受力范围将结构各楼层的质量按比例集中于梁、柱交点，见图2。其中：边梁-边柱节点集中质量为m1，标准值m1k=17.93 t；中梁-中柱节点集中质量为m2，标准值m2k=29.55 t。

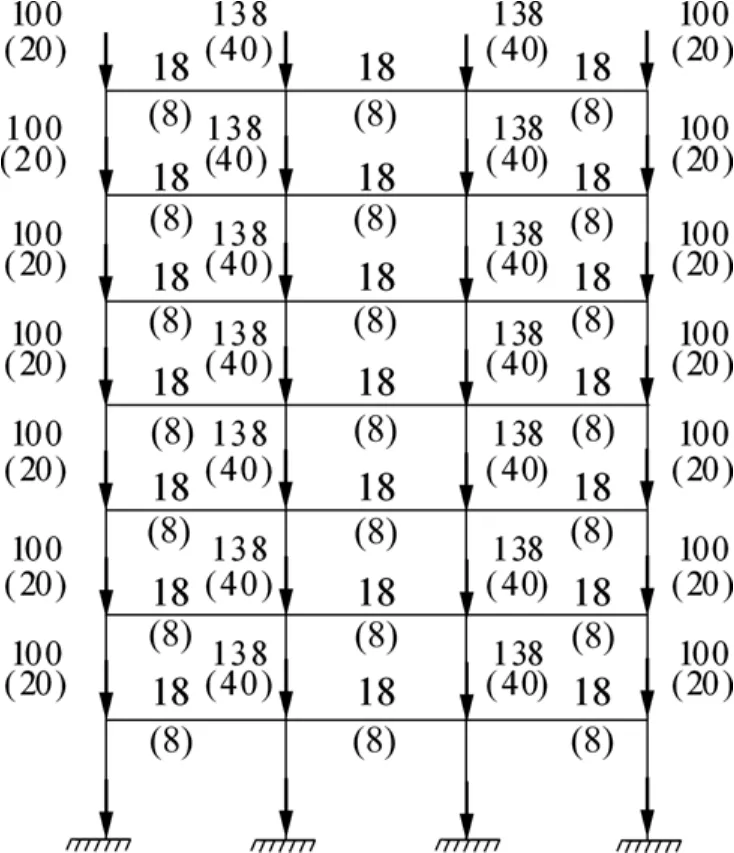
图2 框架荷载标准值Fig.2 Standard load of frame

假定结构的非线性变形集中于梁、柱端部，采用SAP2000提供的集中塑性模型(纤维铰)模拟梁、柱端部的弯矩-曲率(转角)非线性关系。纤维铰模型需要先定义材料的单轴应力-应变关系，为此，进行如下规定：(1) 梁内轴力很小，因而可不考虑箍筋约束对混凝土强度及变形性能的影响，故采用Kent-Park模型[16]模拟梁内混凝土的应力-应变关系，见图3(a)；(2) 柱内轴力较大，因而需要考虑箍筋约束对混凝土强度及变形性能的提高，故采用 Park模型[16](即改进后的Kent-Park模型)模拟柱内混凝土的应力-应变关系，见图3(a)；(3) 采用双线性滞回模型钢筋的应力-应变关系，见图 3(b)。图 3中：σc为混凝土压应力；fc为混凝土抗压强度；εc为混凝土压应变；ε0为混凝土轴心抗压强度对应的压应变；ε50u为无约束混凝土 50%抗压强度对应的压应变；ε50为约束混凝土50%抗压强度对应的压应变；ε20为约束混凝土20%抗压强度对应的压应变；ε50h=ε50-ε50u；K为约束混凝土抗压强度提高系数；σs为钢筋压应力；εs为钢筋压应变；fy为钢筋屈服强度；Es为钢筋弹性模量；α为钢筋屈服后弹性模量比。

采用Releigh阻尼假定，假定结构的阻尼C与其质量M和刚度K成比例，即：C=aM+bK。其中：

式中：T1和T2分别为结构的一阶、二阶特征周期，对应于结构的前 2阶弹性振型，模态分析结果表明，T1=1.109 9 s，T2=0.364 8 s；1ξ和2ξ分别为结构的前2阶模态阻尼比。

进行时程分析时，将积分步长设为场地运动时间步长的1/4，采用Newmark β方法进行数值计算，控制参数γ和β分别取为0.50和0.25，此时，Newmark β法等效于平均常加速度法，算法无条件稳定。

2.3 敏感性分析结果

选择4种能体现混凝土框架结构抗震性能的地震需求参数(EDP)进行敏感性分析，即分析结构的基底剪力需求S、最大楼层加速度需求A、顶点位移需求D和最大层间位移比需求R。上述参数中，前2种属于传统地震力的范畴，而后2种则属于位移反应。

2.3.1 FOSM法分析结果

根据FOSM法对所选4种EDP进行敏感性分析，结果见表4。需注意的是：

(1) 为了便于比较，表4已将EDP对各随机变量的敏感性值(σEDP)统一按其均值进行了归一化处理，即表示为变异系数的形式。

(2) 为确保式(8)中的扰动cp取值合理，对cp分别为0.100，0.010和0.001时的敏感性进行分析，结果如表4所示。经对比分析可知：当cp为0.001时，可确保FOSM方法的计算结果收敛。

(3) 表4中各EDP对PGM的敏感性根据数理统计方法得到。具体步骤如下：首先，将除PGM以外的其他所有随机变量设置为其均值；随后将统一缩放后(PGA=1.74 m·s-2)53条地面运动加速度记录输入结构进行动力时程分析，以获取4组EDP样本(S，A，D和 R)；在此基础上，分别对各组 EDP样本进行统计分析，得其均值、标准差和变异系数，见表4。

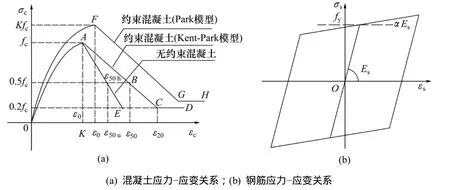
图3 混凝土和钢筋的应力-应变关系Fig.3 Stress-strain relationship of concrete and reinforced bar

表4 结构地震需求参数EDP 的变异系数Table 4 Coefficient of variation of structural EDP %

由表4可知：4种EDP对PGA和PGM的敏感性明显比其他结构特性方面的随机变量的敏感性强。这主要是因为在50 a设计基准期内，场地运动自身的变异性本来就较高；另一方面，结构的位移需求参数往往显示出比另外2种力需求参数更强的随机性，其中D和R的变异系数最高时均超过100%(由PGA引起)，分别达到 105.1%和 108.3%。上述现象表明：结构位移需求参数对其抗震性能的影响不容忽视。

2.3.2 Tornado图形法分析结果

Tornado图形法要求事先根据输入变量的概率分布确定其上、下限(见图 1)，而场地运动的具体特征(PGM)并不是1个简单的随机变量，也没有明确的概率分布函数，因此，本文采用如下方法确定PGM的上、下限(超越概率分别为10%和90%)。

(1) 将所有结构特性方面的不确定因素(随机变量)设置为其均值；

(2) 将所有地面运动加速度记录统一缩放至PGA=1.74 m·s-2(均值)；

(3) 采用缩放后的记录对结构进行动力时程分析以获得一组符合要求的地 震需求参数(如基底剪力、顶点位移和层间位移比等)；

(4) 对地震需求参数进行统计分析，绘出其频数直方图；据直方高度÷总频数÷直方宽度，将其中点相连即为该参数的经验概率密度函数，见图4(a)；

(5) 对地震需求参数的经验概率密度函数进行数值积分以确定其上限(超越概率10%)、均值和下限(超越概率90%)，见图4(b)；与之相应的地震记录具有地震动特征的上限、均值和下限。

图5列出了采用Tornado图形法对不同的地震需求参数(EDP)进行敏感性分析的结果，图中垂线表示将所有不确定性因素设置为其均值时的EDP值。水平条带(即所谓幅摆)的宽度体现了EDP对于相应不确定性因素的敏感性。

由图5可知：对于就所选的4种EDP，PGA对应的幅摆宽度总是最大，PGM对应的幅摆宽度仅比 PGA的小，这表明EDP的不确定性对场地运动的强度及具体特征最为敏感，这与FOSM法的分析结果相吻合。除 PGA和 PGM以外，其他随机变量(fc，fy，Ec，Es，DA，Ms和d)对应的幅摆宽度较窄，且其排列顺序也随EDP的不同而有所变化，但DA，Ms和fc这3个随机变量对应的幅摆宽度一般总能排入前 3～5位(结构顶点位移需求对应的情况略有差别)。这表明在结构特性方面，EDP对于结构阻尼、质量和混凝土抗压强度这3种不确定性因素较敏感，而对其他因素的敏感程度则较低。

图4 EDP的经验概率密度函数及其限值Fig.4 Empirical probability density function and its limit values of EDP

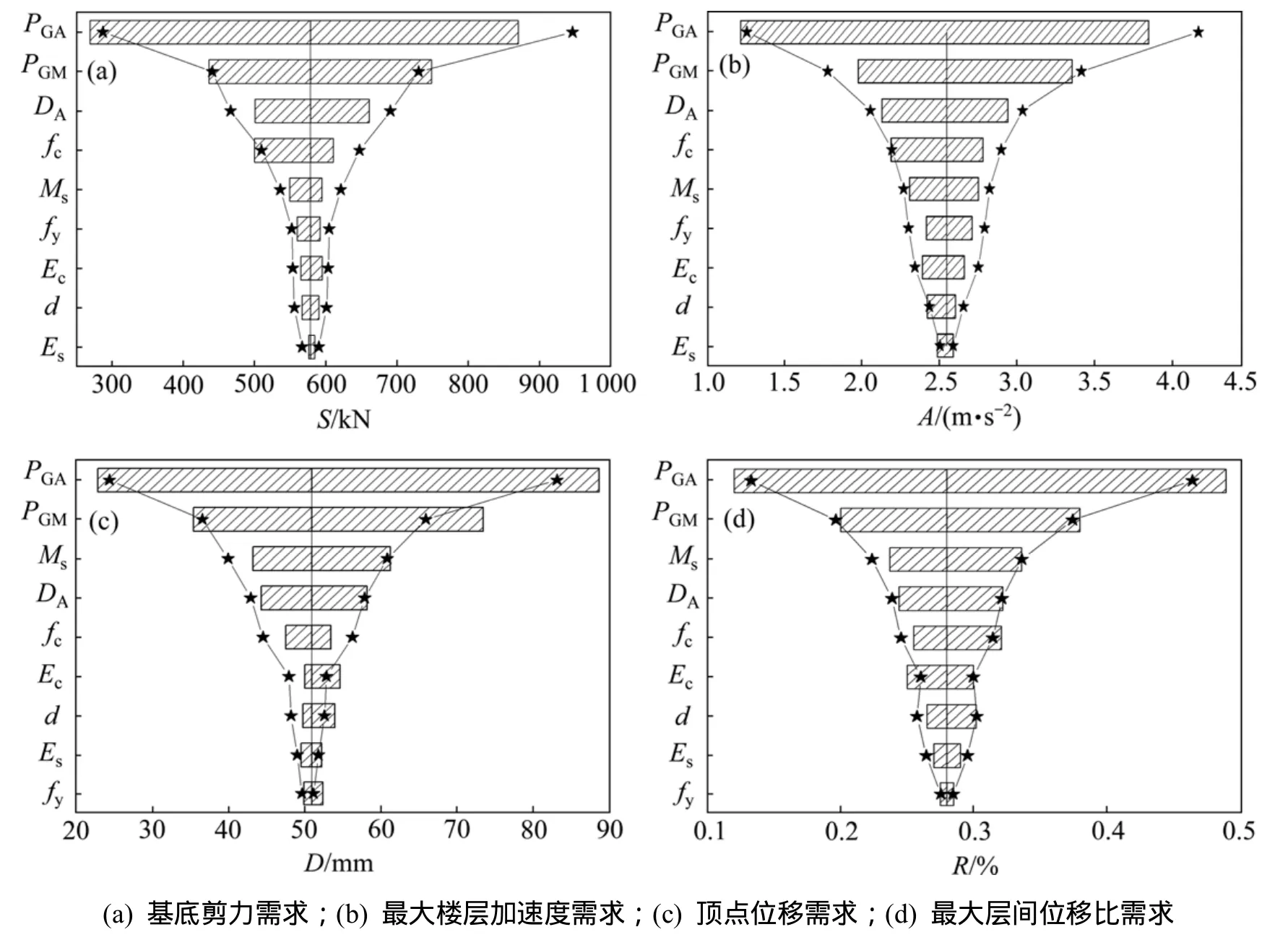
图5 EDP的Tornado图形法和FOSM法敏感性分析结果Fig.5 Analysis results of EDP derived from Tornado diagram method and FOSM method

2.3.3 敏感性分析结果的比较

本文主要采用FOSM法和Tornado图形法进行敏感性分析(数理统计方法仅用于计算EDP对于PGM的敏感性)，这 2种方法都有其各自的优点和局限性。FOSM法能估计出EDP的2个统计量(均值和标准差)，但该方法仅对于线性的输入输出关系才能严格成立。Tornato图形法计算简单，且对于线性和非线性的输入输出关系均可适用，但该方法无法提供任何有关EDP的统计信息。

为了更好地比较这2种方法的分析结果，这里将FOSM法的分析结果也表示成Tornado图形的形式，为此假定地震需求参数与输入随机变量具有相同的概率分布类型，见文献[6]，例如：若PGA服从极值Ⅱ型分布，则假定与之对应的地震需求参数也服从极值Ⅱ型分布。由于地震动的特征PGM不是1个简单的随机变量，前面也未采用概率函数的形式描述其不确定性，这里假定与之对应的地震需求参数服从对数正态分布，与文献[6，17-18]中采用的假定基本一致。

在上述分布假定基础上，结合FOSM法的分析结果(地震需求参数的均值和标准差)，即可确定地震需求的假想概率分布函数，并以此为基础计算超越概率分别为10%和90%时的地震需求上、下限。将地震需求上、下限绘于图中，就能用类似于Tornado图形的形式表示FOSM法的分析结果，见图5中星号包络线。

图5表明：对于各随机变量的敏感性排序，采用这2种方法得到的结果几乎相同，唯一的例外是最大层间位移比对Ec和d这2随机变量的敏感性排序(见图5(d))。但考虑到Ec和d的效应很小(幅摆较窄)，因此，出现一定偏差不至于对分析结果产生决定性影响。总的来说，采用这2种方法得到的敏感性排序体现出很强的一致性，这直观地验证了上述分析结果，也表明分析方法合理。

3 结论

(1) 以1个典型混凝土框架结构为例，采用一次二阶矩法、龙卷风图形法和数理统计法这3种敏感性分析方法，估计了4种结构地震需求参数对于基本不确定因素的敏感度，进而对基本不确定因素的重要性进行排序，从中选择对地震需求的不确定性产生显著影响的敏感性因素。

(2) 地震需求参数的不确定性受场地运动强度的影响最显著，其次为场地运动的具体特征。除上述 2最主要因素外，EDP对结构特性方面3种不确定因素(黏性阻尼、质量和混凝土抗压强度)的敏感程度较高，而对其他因素不太敏感。

[1] Porter K A, Beck J L, Shaikhutdinov R V. Sensitivity of building loss estimate to major uncertain variables[J]. Earthquake Spectra,2002, 18(4): 719-743.

[2] Bake J W, Cornell C A. Uncertainty specification and propagation for loss estimation using FOSM methods[R].Berkeley: University of California. Pacific Earthquake Engineering Research Center, 2003: 68-82.

[3] Aslani H, Miranda E. Probabilistic response assessment for building-specific loss estimation[R]. Berkeley: University of California. Pacific Earthquake Engineering Research Center,2003: 38-56.

[4] IS 02394, General Principles on reliability for structures[S].

[5] GB 50068—2001, 建筑结构可靠度设计统一标准[S].GB 50068—2001, Unified standard for reliability design of building structures[S].

[6] Hyung T L. Probabilistic seismic evaluation of reinforced concrete structural components and systems[D]. Berkeley:University of California. Department of Civil and Environmental Engineering, 2005: 138-161.

[7] Vidic T, Fajfar P, Fischinger M. Consistent inelastic design spectra: Strength and displacement[J]. Earthquake Engineering and Structural Dynamics, 1994, 23: 507-521.]

[8] 尹犟. 混凝土结构地震需求估计方法研究[D]. 长沙: 湖南大学土木工程学院, 2011: 86-90.YIN Jiang. The study of seismic demand estimation method of reinforced concrete structures[D]. Changsha: Hunan University.College of Civil Engineering, 2011: 86-90.

[9] 高小旺, 鲍霭斌. 地震作用的概率模型及统计参数[J]. 地震工程与工程振动, 1985, 5(1): 13-21.GAO Xiao-wang, BAO Ai-bin. Probabilistic model and its statistical parameters for seismic load[J]. Earthquake Engineering and Engineering Vibration, 1985, 5(1): 13-21.

[10] Vrouwenvelder T. The JCSS probabilistic model code[J].Structural Safety, 1997, 19(3): 245-251.

[11] MirzA S A, Hatzinikolas M, Macgregor J G. Statistical descriptions of strength of concrete[J]. Journal of Structural Division, 1979, 105(6): 1021-1037.

[12] Mirza S A, Macgregor J G. Variability of mechanical properties of reinforced bars[J]. Journal of Structural Division, 1979,105(5): 921-937.

[13] 胡晓鹏, 牛狄涛, 薛国辉. 住宅结构抗力的调查与统计分析[J]. 哈尔滨工业大学学报, 2008, 40(6): 978-981.HU Xiao-peng, NIU Di-tao, XUE Guo-hui. Investigation and statistical analysis on resistance of residential buildings[J].Journal of Harbin Institute of Technology, 2008, 40(6):978-981.

[14] GB 50010—2002, 混凝土结构设计规范[S].GB 50010—2002, Code for design of concrete structures[S].

[15] GB 50011—2001, 建筑抗震设计规范[S].GB 50011—2001, Code for seismic design of buildings[S].

[16] 欧进萍, 段宇博, 刘会仪. 结构随机地震作用及其统计参数[J]. 哈尔滨建筑工程学院学报, 1994, 27(5): 1-9.OU Jing-ping. DUAN Yu-bo, LIU Hui-yi. Structural random earthquake action and its statistical parameters[J]. Journal of Harbin Architectural and Civil Engineering Institute, 1994, 27(5):1-9.

[17] 周文峰, 黄宗明, 白绍良. 约束混凝土几种有代表性应力-应变模型及其比较[J]. 重庆建筑大学学报, 2003, 25(4): 121-127.ZHOU Wen-feng, HUANG Zong-ming, BAI Shao-liang.Introduction and comparison of several representative confinement models for concrete[J]. Journal of Chongqing Architecture University, 2003, 25(4): 121-127.

[18] Bazzurro P. Probabilistic seismic demand analysis[D]. Stanford:Stanford University. Department of Civil and Environmental Engineering, 1998: 151-162.

[19] Jalayer F. Direct probabilistic seismic analysis: implementing non-linear dynamic assessments[D]. Stanford: Stanford University. Department of Civil and Environmental Engineering,2003: 201-220.