浓相气固流化床悬浮体黏度的计算模型

吕波，骆振福，张博，陈霞，李晓明

(中国矿业大学 化工学院，江苏 徐州，221116)

由于浓相气固流化床具有在流化状态下所形成的气固悬浮体的类流体特性，从而能够使矿物质按密度不同进行分选。更重要的是，它能在无水的条件下有效地进行分选作业，因此，在我国广大的缺水及寒冰地区具有很好的发展前景。众所周知，矿物在流化床层中的运动规律与分选效果相关。而在矿物的沉降过程中，床层中气固悬浮体的黏度起到了关键性的作用：黏度过高将使得各粒级的沉降速度变慢，干扰沉降加剧，分选效率也随之降低；而黏度过低则会使各粒级在床层中的停留时间变短，难以得到有效分选。因此对于浓相气固流化床悬浮体黏度的研究十分必要[1-5]。但由于浓相气固流化床床层是有多相质混合而成，因此床层中存在着颗粒与颗粒、颗粒与空气的相互作用，这些作用力不仅包括流体外部力如流体曳力、Basset力、Magnus力等，还包括颗粒间的静电力、碰撞力、摩擦力等[6-7]。这些作用力使得浓相气固悬浮体的黏度的测定工作变得较为复杂。

浓相气固流化床的流化床层可以看作为颗粒与空气流所形成的浓相气固悬浮体，其属于非牛顿流体范畴，因此经典的牛顿流体力学公式已经不适应于浓相气固悬浮体流变性的分析与计算。并且由于非牛顿流体的复杂性，不能直接套用牛顿流体的黏度定义，非牛顿流体的黏度可表现为剪切速率或悬浮液性质(包括颗粒性质)公式。关于其黏度的测定，已有大量的学者进行了研究。经典的Einstein模型建立在高稀相悬浮液(体积分数φ＜2%)的基础上，由于其没有考虑到颗粒之间的相互作用力，因此它属于一种理想状态下的模型，对实际的黏度估算没有什么实际意义。为弥补这一缺陷，Batchelor等[8-10]先后对Einstein模型进行了改进与完善。这些改善后的模型比经典的Einstein模型多出了φ的更高次项，从而将颗粒间的作用力考虑到模型中。另一方面，Krieger等[11]采用使邻近颗粒的影响平均化的技术对Einstein模型改进行了改进。φm作为这个新的影响因子被考虑到流变性模型之中，这里，φm被定义为颗粒的最大体积分数(η→∞)，它与颗粒的粒度分布、颗粒的尺寸与大小等颗粒性质有关。一般情况下，φm在实验过程中都为常数，因此一些实验设计者都把φ/φm作为一个整体来加以考虑。在近几年的悬浮液流变性研究中，φm被或多或少引用到实验模型设计中[12-17]。例如，利用Arefinia等[12]在测量铝以及高氯酸铵分别分散在端羟基聚丁二烯所形成的复合悬浮液的黏度时所提出的Arefinia模型，Amini等[13]结合数学回归模型，利用(φ/(φm-φ))作为模型因素，针对陶瓷浆料的黏度测定提出了Amini Horri模型等。

然而，上述黏度模型大多建立在物料颗粒粒级较小(1 μm左右)、所构成的悬浮液浓度较低的基础上，难以适用于测定空气重介质流化床中磁铁矿(粒径在0.3～0.074 mm之间)形成的浓相气固悬浮体的黏度。本文作者利用理论模型结合实际实验测定结果推导出的黏度模型，对于空气重介质流化床床层黏度的测定具有很好的适应性。

1 实验

1.1 实验装置

为了测定流化床中浓相气固悬浮体的黏度，设计了如图1所示的实验模型系统。整个实验系统主要分为2个部分，即流化床模型和黏度测量系统。

流化床模型的床体为有机玻璃制成的圆柱体(直径为170 mm，高为500 mm)制成，以便通过床壁上的标尺来观察和测定流化床的床层高度。同时可通过阀门来控制加入流化床中气体的流量，以此来实现不同的空隙率下的流化床床层，并测定各自的床层黏度。针对浓相气固流化床中重介质所形成的非牛顿悬浮体黏度的测定，大量文献中利用搅拌叶轮、钢球以及球形颗粒或气泡的终端速度和垂直的旋转圆柱体等，但是上述测量系统大多适用于固液悬浮体，且由于测量元件的干扰使得测量的精度不高。故在本实验中，采用了NDJ-1旋转黏度计，测定流化床所形成的非牛顿悬浮体黏度，由于该黏度计转子半径较小(最小可达至6 mm)，因此它对于流化床流化过程干扰较小，

测量精度较高。

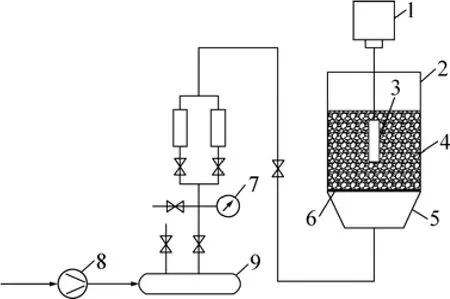
图1 空气重介质流化床的黏度测定装置Fig.1 Experiment device of air heavy medium fluidized bed viscosity

1.2 实验材料

为验证及了解在浓相气固流化床悬浮体黏度的影响因素，分别采用了沙子、玻璃粉以及磁铁矿作为流化床中的流化物料，其物理特性如下表1所示。

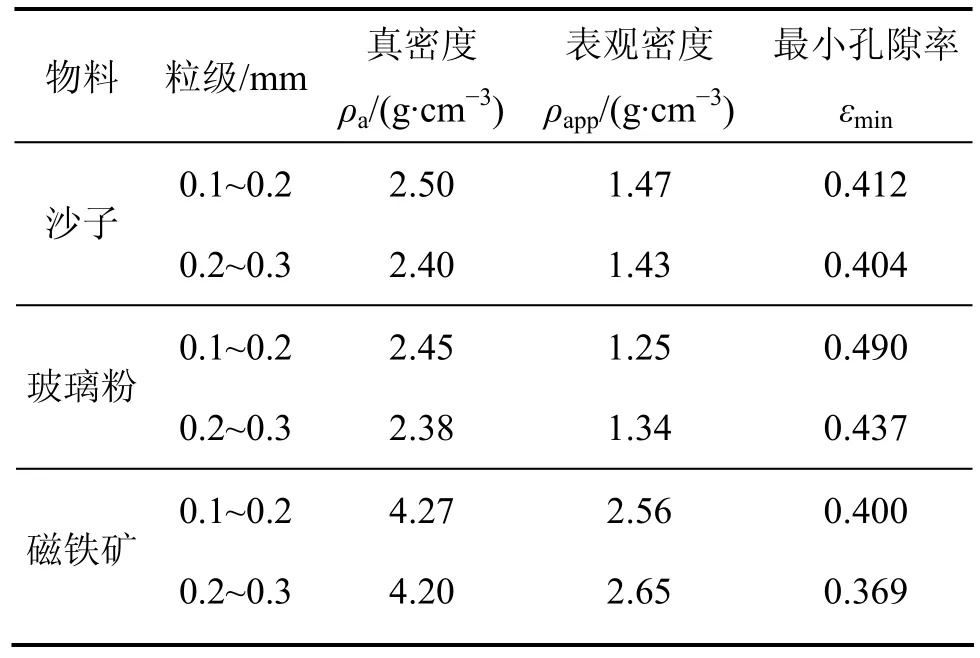
表1 物料的物理特性Table 1 Physical properties of material

在实验前期，为兼顾细粒级的研究工作，采用了-0.1 mm粒级的颗粒作为实验对象，但由于粒径较小，易在流化床中易形成沟流，难以构成均匀稳定的流化床层，导致测量较为困难，故在实验中不予采用。这同时也说明了在选择浓相气固流化床的重介质时，颗粒粒级是一个十分重要的考虑因素。

2 浓相气固流化床悬浮体的黏度测定模型

2.1 黏度-空隙率模型

假设在流化状态下，流化床悬浮液中的各组分都存在着自己的黏度，根据Amini等[13]提出的刚性颗粒悬浮体的黏度假设原理，可得出下面的黏度计算公式：式中：μs为悬浮体的黏度；μf为气体的黏度；ε为床层的空隙率；μres为悬浮液的残余黏度。

董景山等[18]在进行流体热物理性质的计算中曾提出了残余黏度的计算公式：

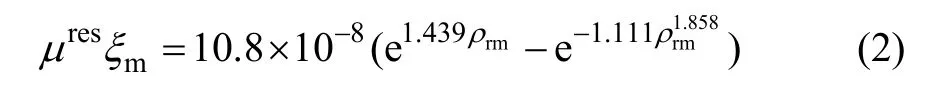
式中：ξm为混合物的黏度参数；ρrm为混合物的相对密度(即混合物的密度与临界密度的比值)。

针对浓相气固流化床，流化状态下床层颗粒悬浮体的残余黏度公式为：

式中：εi为床层相对空隙率，εi=ε/εmin，εmin为最小空隙率。a和b为流化床悬浮体黏度参数，可由实验拟合得出。结合式(1)和(3)可得出床层的黏度计算公式为：

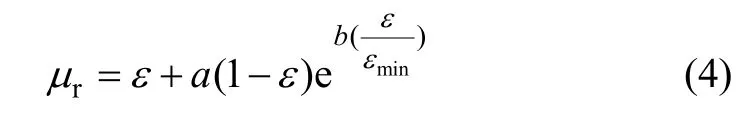
其中，μr为床层相对黏度，为流化床悬浮体黏度与空气黏度的比值。

2.2 最小空隙率εmin的测定

最小空隙率εmin指颗粒群在压实状态下的空隙率，其值与颗粒的物理特性(包括粒径、形状、密度等)有关。根据空隙率的概念可知：

式中：φmax为悬浮体中物料的最大填充率。φmax的测定方法主要有Mayadunne等[9]所采用的图解法、Lee[19]的模型、Yu等[20]的直线混合填充模型等，但是利用这些模型计算φmax的过程较为复杂。Arefinia等[12]提了一种较为简单的最大填充率的计算公式：

式中：ρapp和ρa分别为颗粒的表观密度与真密度。结合式(5)和(6)，得出最小空隙率的计算公式为：

3 结果与讨论

3.1 黏度的影响因素

在浓相气固流化床中，重介质物理特性不仅与流化床的流化质量(包括床层黏度)相关，还在实际生产过程中涉及到产品的脱介以及介质的回收等问题。因此，在研究流化床悬浮体黏度的影响因素时，必须考虑物料的物理特性。图2所示为不同物料所形成的悬浮体黏度。

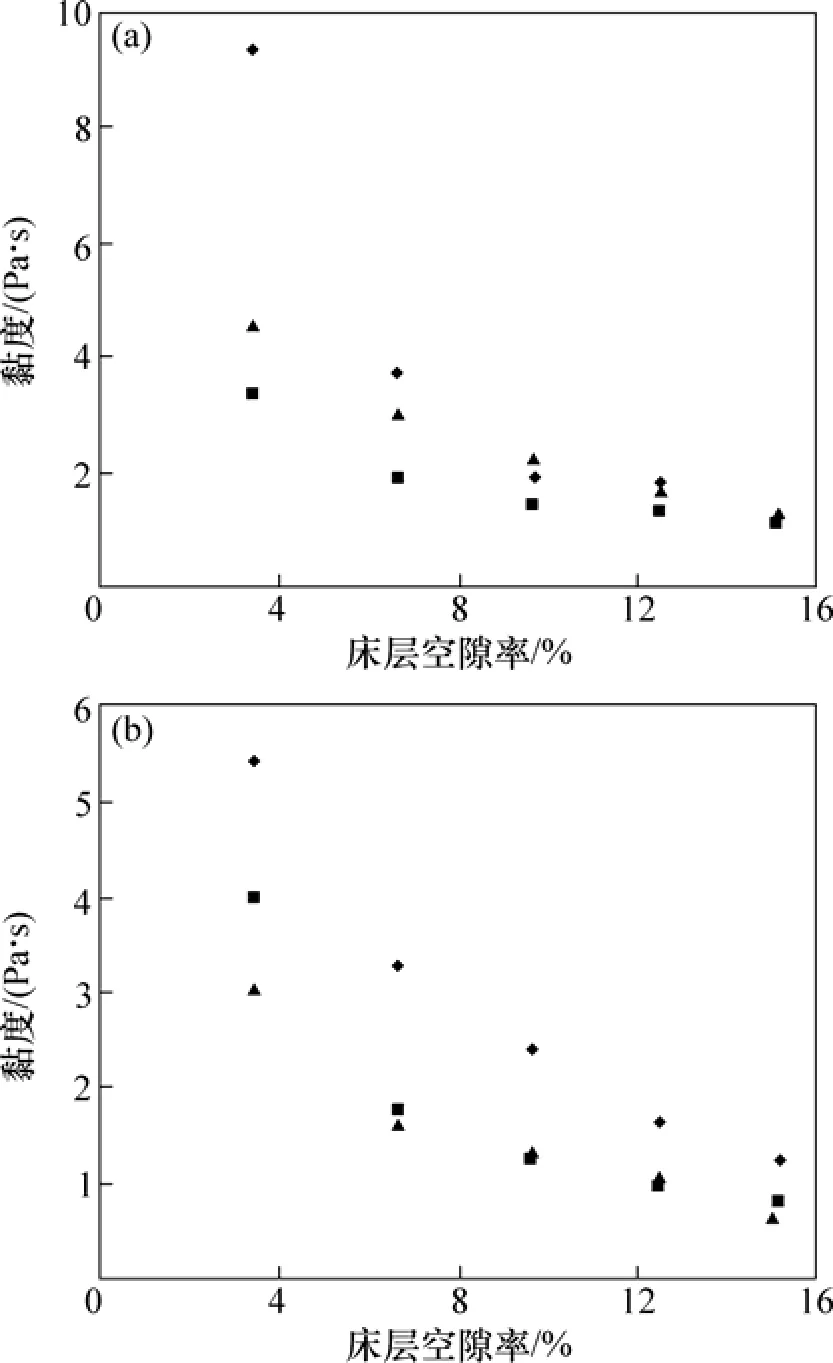
图2 粒级为0.1～0.2和0.2～0.3 μm的颗粒悬浮体黏度Fig.2 Viscosity of particles suspension with diameters of 0.1-0.2 μm and 0.2-0.3 μm

由图2可知，密度较大的颗粒其黏度也较大，这主要是对于密度较大的颗粒，必须给予足够的气体流量才能托起床层，因此在同等床层空隙率下，床层中的气体与颗粒之间的运动较为激烈，对转子的作用力较大，使其测量黏度也随之提高。

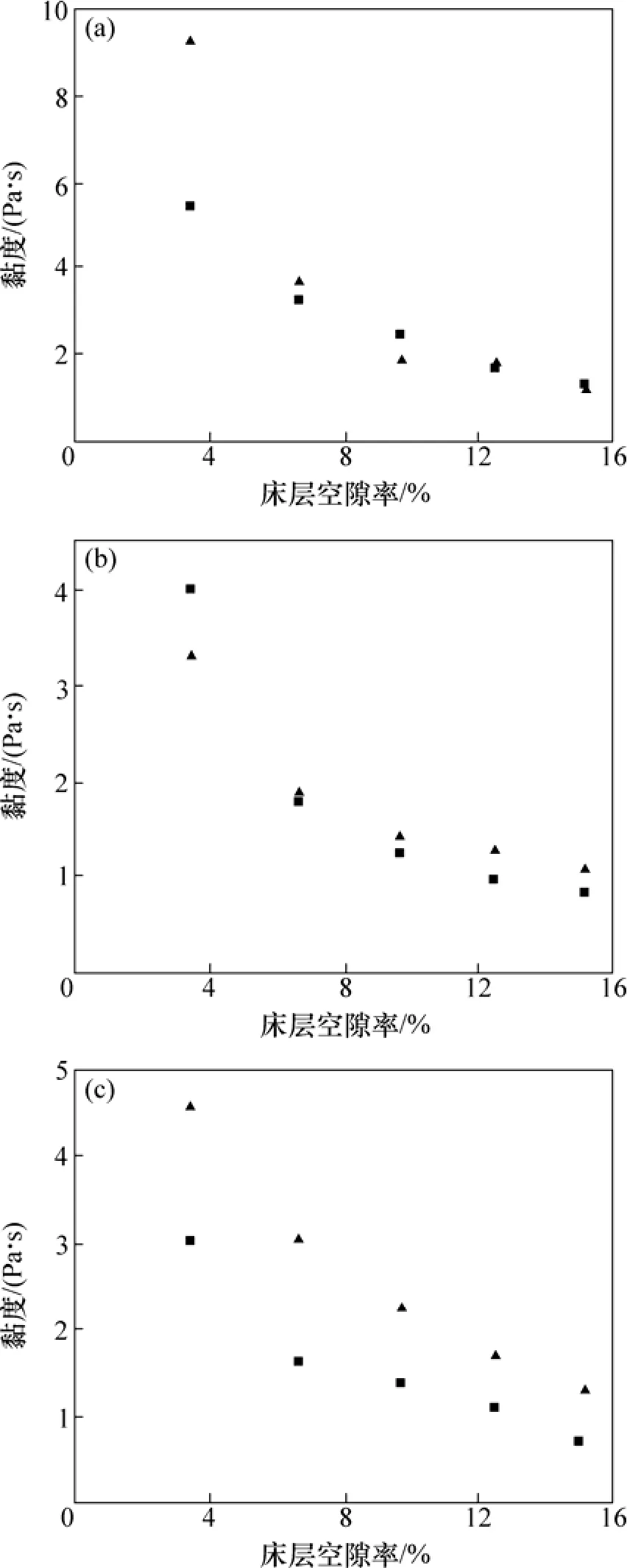
图3 不同粒径对悬浮体黏度的影响Fig.3 Effect of grain size on viscosity of suspension

不同粒径对流化床悬浮体黏度的影响如图3所示。从图3可以看出：粒径与流化床悬浮体黏度成正比。在空隙率小于13%时，随着粒径的增加，物料所形成的悬浮体黏度也随之增加。但是，在空隙率大于13%后，流化床悬浮体黏度随粒径的变化较为缓和，基本处于同一的趋势。这是由于空隙率较大时，其床层中气体含量较多，相对于气相而言，固相甚至可忽略不计，此时颗粒对于黏度的影响较小。当床层的空隙率达到最大值时，床层将变得及不稳定，甚至会导致喷涌现象的产生，这对浓相气固流化床来说是必须要杜绝的情况。

3.2 床层的相对空隙率

为了定量表征颗粒的物理特性，引入最小空隙率表示不同颗粒的物理特性，其可代替复杂的颗粒物理性质作为悬浮体黏度的影响因素之一。在悬浮体黏度的测量模型中，采用相对孔隙率，来表现最小孔隙率与黏度的关系。相对空隙率与黏度的关系如图4所示。由图4可以看出：床层的相对空隙率与悬浮体黏度成反比，并且流化床悬浮体黏度随相对空隙率增加而减少的趋势较为缓和。

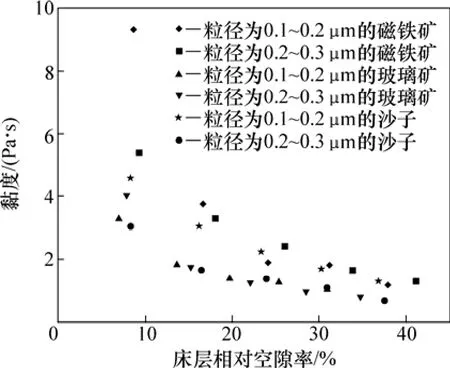
图4 床层相对空隙率与黏度的关系Fig.4 Relationship between relative pore ratio and viscosity

3.3 公式验证

为验证理论模型用于测量浓相气固流化床的黏度的可靠性，并得出用于实际计算的黏度参数，采用了DPS数据处理软件结合计算公式对实验过程中所测定的数据进行分析及拟合处理。图5所示为计算值与测定值的对比。

3种物料在不同粒级条件下所适应的计算公式及方差分析如表2所示。从表2可以看出：黏度参数a大多为2×105～ 5×105，除了粒级为 0.1～0.2 mm的磁铁矿的a达11×105外，参数b则较为稳定，大多为4～5。个别参数跳跃较大的原因，一方面是由于实验过程中所产生的实验误差；另一方面是由于流化床床层在偏离最小流化气速的操作条件下变得极不稳定，这对床层黏度测量工作造成了很大的负面影响。这同时也说明了，浓相气固流化床在实际操作过程中，要调节好气速条件，以便使床层达到较好的流化状态。

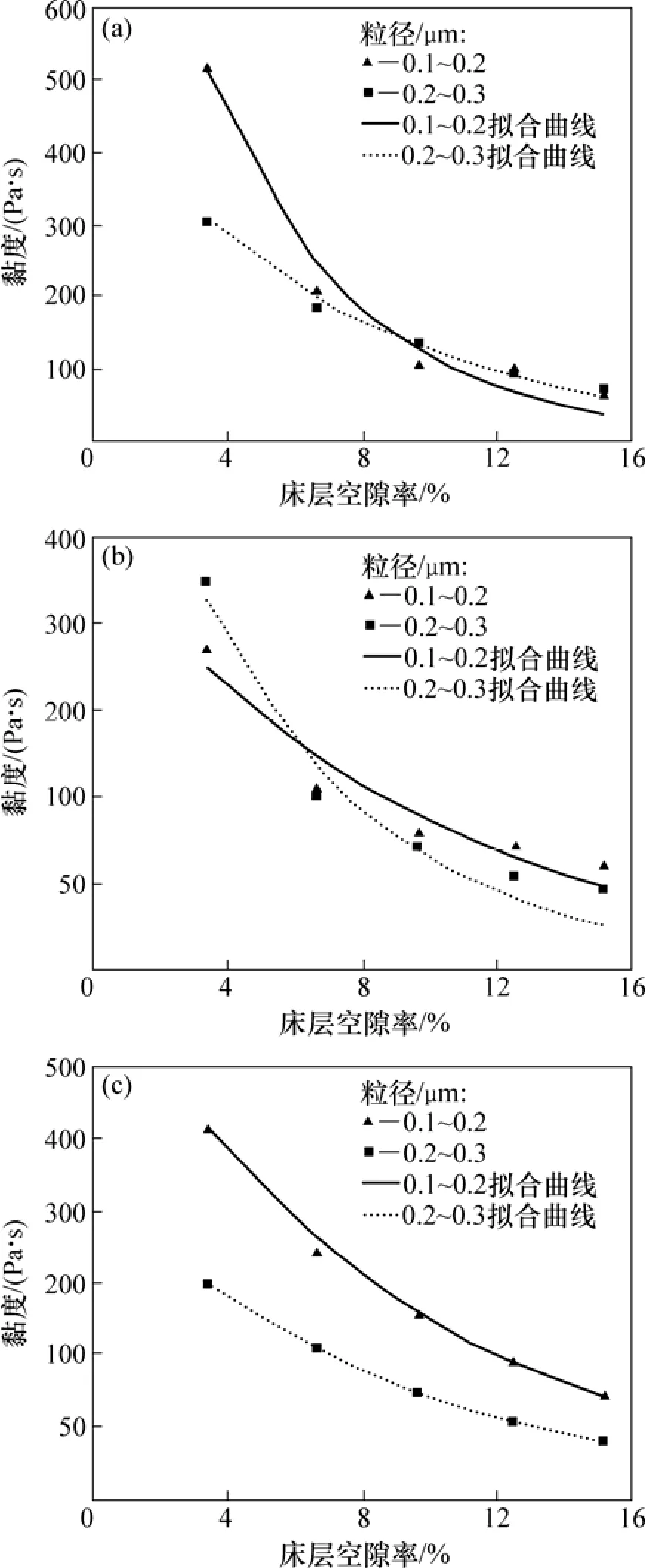
图5 悬浮体黏度拟合曲线Fig.5 Fitting curve of viscosity of suspension

利用表2中公式所得黏度计算值与实际测量值进行比较可知：两者变化趋势一致，吻合度较高，而且拟合曲线相关系数R2最大为0.99，这说明理论所得的黏度计算模型能够很好地用于估算流化床悬浮体黏度。

表2 流化床悬浮体黏度计算公式Table 2 Calculation formulas of suspension’s viscosity

4 结论

(1) 随着颗粒粒度或密度的减少，气固流化床中所形成的气固悬浮体的黏度降低；随床层空隙率的减少黏度逐渐增加。

(2) 根据理论推导得出一个适用于浓相气固悬浮体黏度测定的两元素计算模型，其计算值与实际的测量值吻合较好，其相关系数R2最大为0.99。此模型对于实际的流化床层中浓相气固悬浮体的黏度测定具有很好的指导意义。

[1]徐守坤, 管玉平, 陈清如. 空气重介质流化床气泡行为及其对分选的影响[J]. 中国矿业大学学报, 2001, 30(3): 268-271.XU Shou-kun, GUAN Yu-ping, CHEN Qing-ru. The bubbles behavior of the air heavy medium fluidized bed and its influence to the separation[J]. Journal of China University of Mining &Technology, 2001, 30(3): 268-271.

[2]陶秀祥, 陈增强, 杨毅, 等. 深床型流化床块煤选矸的试验研究[J]. 中国矿业大学学报, 2001, 30(6): 527-530.TAO Xiu-xiang, CHEN zheng-qiang, YANG Yi, et al. The experimental study on the separation of lump coal by the deep bed-type fluidized bed[J]. Journal of China University of Mining& Technology, 2001, 30(6): 527-530.

[3]ZHAO Yao-min, WEI Lu-bin. Rheology of gas-solid fluidized bed[J]. Fuel Processing Technology, 2000, 68: 153-160.

[4]ZHAO Yao-min, LIU Jiong-tian, WEI Xian-yong, et al. New progress in the processing and efficient utilization of coal[J].Mining Science and Technology, 2011, 21(4): 463-468.

[5]骆振福, 赵跃民, 陈清如, 等. 浓相高密度分选流化床气体分布参数的研究[J]. 中国矿业大学学报, 2004, 33(3): 237-240.LUO Zhen-fu, ZHAO Yue-min, CHEN Qing-ru, et al. Research on gas distribution of dense phase high density fluidized bed for separate ion[J]. Journal of China University of Mining &Technology, 2004, 33(3): 237-240.

[6]李佑楚. 流态化过程工程导论[M]. 北京: 科技出版社, 2008:5-25.LI You-chu. Fluidized process engineering introduction[M].Beijing: Science & Technology Press, 2008: 5-25.

[7]曾凡, 胡永平. 矿物加工颗粒学[M]. 徐州: 中国矿业大学出版社, 1995: 178-197.ZEN Fan, FU Yong-ping. Partical technology of mineral processing[M]. Xuzhou: China University of Mining &Technology Press, 1995: 178-197.

[8]Batchelor G K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles[J]. Fluid Mech, 1977, 83:97-117.

[9]Mayadunne A, Bhattacharya S N, Kosior E. Modelling of packing behavior of irregularly shaped particles dispersed in a polymer matrix[J]. Powder Technology, 1996, 89(2): 115-127.

[10]Hush C H, Becher P H. Effective viscosity of spheres[J]. Journal of the American Ceramic Society, 2005, 88: 1046-1049.

[11]Krieger I M, Dougherty T J. A mechanism for non-Newtonian flow in suspensions of rigid spheres[J]. Trans Soc Rheol,1959(3): 137-152.

[12]Arefinia R, Shojaei A. On the viscosity of composite suspensions of aluminum and ammonium perchlorate particles dispersed in hydroxyl terminated polybutadiene: New empirical model[J].Journal of Colloid and Interface Science, 2006, 299: 962-971.

[13]Amini H B, Ranganathan P, Cordelia S, et al. A new empirical viscosity model for ceramic suspensions[J]. Chemical Engineering Science, 2011, 66: 2798-2806.

[14]Mooney M. The viscosity of concentrated suspension of spherical particles[J]. Journal of Colloid Science, 1951, 6(2):162-170.

[15]Oliver D R, Ward S G. Relationship between relative viscosity and volume concentration of stable suspensions of spherical particles[J]. Nature, 1953, 171: 396-397.

[16]Chong J S, Christiansen E B, Baer A D. Rheology of concentrated suspensions[J]. Journal of Applied Polymer Science,1971, 15: 2007-2021.

[17]Brouwers H J H. Viscosity of a concentrated suspension of rigid monosized particles[J]. Physical Review, 2010, 81(5):051402-1-051402-11.

[18]童景山, 李敬. 流体热物理性质的计算[M]. 北京: 清华大学出版社, 1982: 186-245.TONG Jing-shan, LI jing. Fluid thermo physical properties calculation[M]. Beijing: Tsinghua University Press, 1982:186-245.

[19]Lee D I. Packing of spheres and its effect on the viscosity of suspension[J]. Journal of Paint Technology, 1970, 42: 579-584.

[20]Yu A B, Standish N. Estimation of the porosity of particle mixtures by a linear-mixture packing model[J]. Industrial Engineering Chemistry Research, 1991, 30: 1372-1385.