激励信号对地－空瞬变电磁响应的影响分析

关珊珊 林 君 嵇艳鞠 阳贵红 张晓爽王 远 万 玲 陈曙东

（吉林大学地球信息探测仪器教育部重点实验室，吉林 长春130026）

引 言

地－空电磁探测系统（GREATEM），也称为半航空电磁系统，采用地面发射、空中接收的方式，因此它同时具有航空和地面瞬变电磁系统的优点。同地面瞬变电磁系统相比，它具有野外布线方便快捷、探测高效等优势；较航空瞬变电磁系统，具有信噪比更高、空间分辨率更好、勘探深度更深的优点，可快速实现较大面积内深部异常体的探测，较适用于我国地形复杂的山区资源探测。

最早的地－空电磁探测系统（TURAIR）出现在20世纪70年代的加拿大和俄罗斯，它是一种频率域的电磁探测系统。发射线圈直接由发电机供电，但是在文献中并没有明确说明激励场的波形。1991－1993年间，由澳大利亚研制的固定线圈地－空瞬变电磁系统（FLAIRTEM）和1997年加拿大人研制的地－空电磁探测系统（TerraAir）都是时间域电磁探测系统，激励波形均为方波。所不同的是TerraAir系统进行的是全波形的瞬变电磁响应计算而FLAIRTEM系统只进行了电流关断后的电磁响应计算。在1992年，日本基于地面长偏移距瞬变电磁法（LOTEM）提出了GREATEM系统，它采用接地长导线源发射，感应线圈在空中接收的工作方式，具有布线快速和高效的优点。Richard S.Smith在2001年对航空、半航空和地面电磁系统的数据进行了对比分析［1－5］。

1998年，Guimin Liu［6］研究了磁性源、自由空间下，不同电流发射波形对航空瞬变电磁响应的影响，但仅对电流完全关断后，即电流为零段（off－time段）的电磁响应进行了研究。2006年于生宝等分析了阶跃关断与线性关断早期瞬变电磁响应的区别［7］。2007年嵇艳鞠等进行了浅层瞬变电磁法中全程瞬变场的畸变研究，激励信号是斜阶跃波［8］。2010年，许洋铖等研究了阶跃波关断的航空时域电磁法的初始场计算［9］。2008年 Yin，C.［10］计算了磁性源，发射波形为半正弦波和梯形波的全波形航空感应电动势。

在前面已有研究的基础上，利用地－空系统阶跃波瞬变电磁响应与任意激励波形卷积的方法［10］，研究了电性源，激励波形为方波、半正弦波、三角波和梯形波情况下电流不为零段（on－time段）和offtime段对应高阻异常和低阻异常的地－空瞬变电磁响应影响；并且提出了激励能量概念，通过激励能量大小分析了不同激励波形响应的大小。

1 阶跃波地－空瞬变电磁响应计算

为了计算不同激励波形的地－空瞬变电磁响应，首先需要计算阶跃波关断后的地－空电磁响应。图1为时间域地－空电磁探测系统示意图。接收线圈距地面高30m，接收线圈面积200m2，导线长1 km，电流为200A.

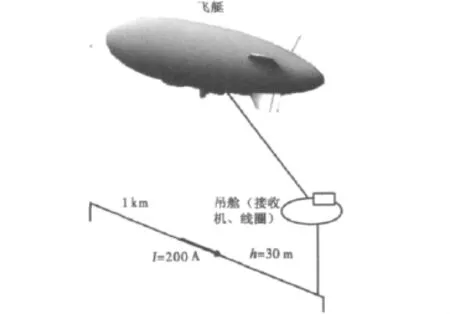
图1 地－空电磁探测系统示意图

纳比吉安给出了有限长接地导线层状大地的频率域磁场垂直分量表达式［11］

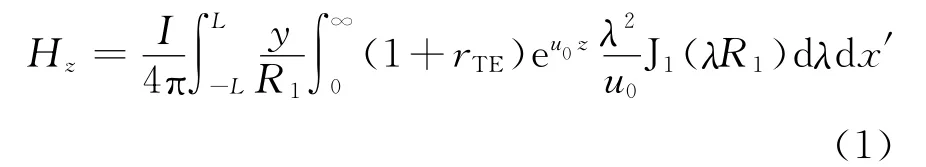
式中u0＝ （λ2－）1／2，在准静态条件下，u0＝λ，因此式（1）可写为

式中：R1＝ ［（x－x′）＋y2］1／2

三层大地反射系数

计算参数说明见表1.

表1 计算参数说明

式（2）中有两重积分，内层积分存在振荡的Bessel函数，一般只能求出均匀半空间的解析式，如果求解两层及以上层状大地的电磁响应需采用数值积分方法。使用 D.Guptasarma和 B.Singh［12－13］提出的数字滤波法解决内层积分的hankel变换问题，而外层积分利用辛普森积分法就可以实现。频率域到时间域的转换是利用D.Guptasarma提出的线性滤波方法，将－iωμ0sHz变化到时间域就得到了感应电动势Nabighian，M.N.和 Oristaglio，M.L.［14］给出了均匀半空间接地导线赤道轴线上感应电动势的解析表达式，将计算结果与式（3）进行对比，以验证算法的正确性。

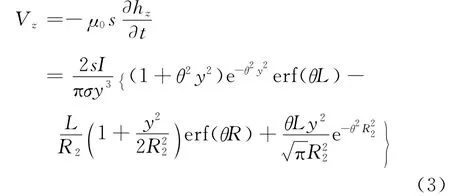
从图2可以看出，应用解析式法和数值积分法计算得出的感应电动势衰减曲线重合的很好。

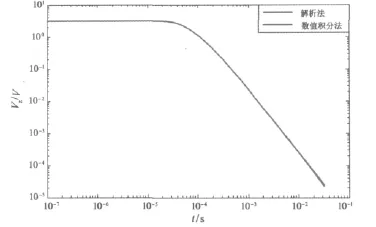
图2 数值积分法响应与纳比吉安解析式响应比对图

2 层状大地任意激励波形响应计算

任意激励波形的瞬变电磁响应为阶跃波瞬变电磁响应与电流一阶导数的卷积，如公式（4）为

式中：V任意（t）为任意波形的瞬变电磁响应；I任意（t）为任意瞬时电流；V阶跃（t）为阶跃波的瞬变电磁响应。结合公式（4）及阶跃波地 －空瞬变电磁响应即可求得层状大地任意激励波形的地 －空瞬变电磁响应，并通过激励能量对瞬变响应进行分析。

2.1 激励波形

图3 激励电流波形

为了计算任意电流波形的瞬变电磁响应，图3给出所需要的四种发射电流波形，其中Ti为激励电流半周期，i＝1，2，3，4分别对应于半正弦波、方波、三角波和梯形波。t1，t2，t4，t7为各激励电流的脉冲持续时间，u（t）为阶跃函数，δ（t）为冲激函数。对应的波形解析式和一阶导数表达式如下：

1）半正弦波

2）方波

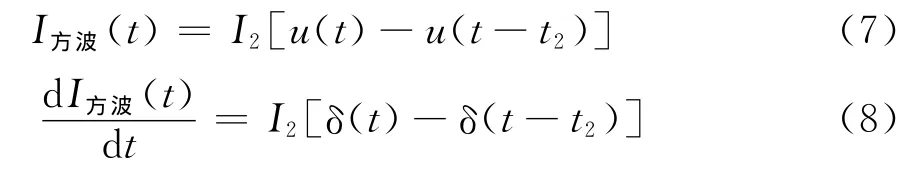
3）三角波

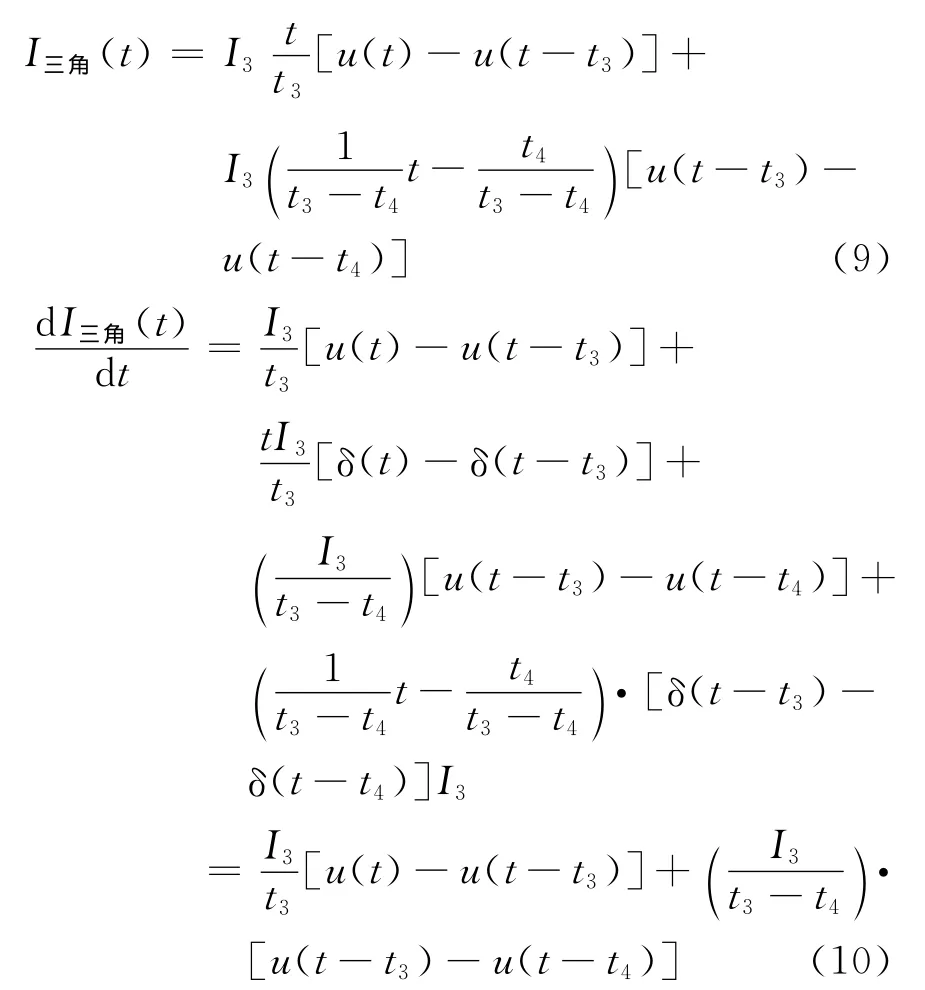
4）梯形波

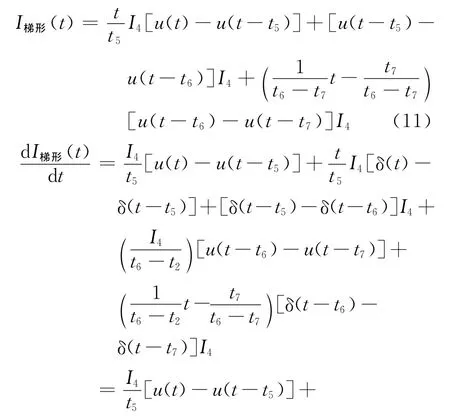
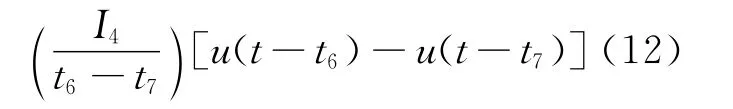
2.2 激励能量与响应大小分析

不论发射机的有限长导线中通入的是哪一种电流，本质上都是一种能量，激励能量的通用表达式为

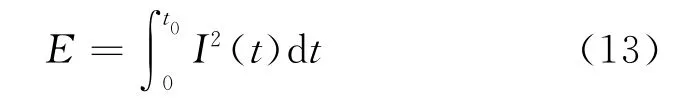
式中：t0为脉冲持续时间；I（t）为发射电流。

半正弦波能量

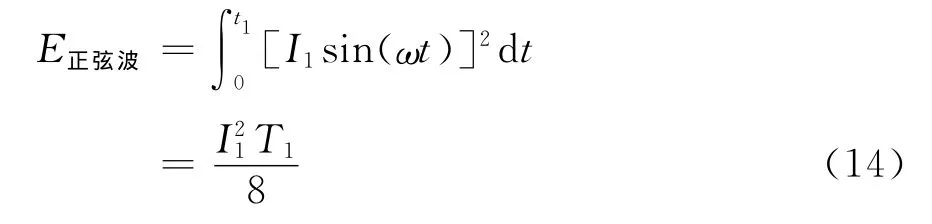
方波能量

三角波能量

梯形波能量

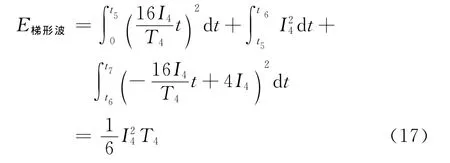
其中脉冲宽度取1／4倍半周期长，脉冲频率f＝25 Hz，因此，四种波形的半周期长均为0.02s.I1、I2、I3、I4分别是正弦波、方波、三角波和梯形波的电流最大值，均取200A.ω为正弦波的角频率。经计算可得各激励能量间关系为

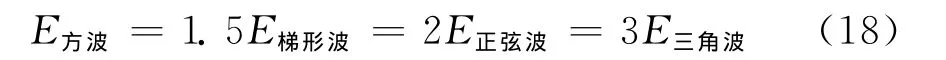
将等式（6）、（8）、（10）、（12）分别与阶跃波的瞬变电磁响应进行卷积，就可得出这四种波形的层状大地瞬变电磁响应，如图4所示。接收位置坐标为（0，100，30），接收线圈匝数为1，第一层电导率σ1＝1／100S／m，第二层电导率σ2＝1／5S／m，第三层电导率σ3＝1／100S／m；第一层大地厚度h1＝100m，第二层厚度h2＝50m.

图4给出了off－time段的瞬变电磁响应。在整个的off－time段，方波的响应是最大的，其次是梯形波和半正弦波，三角波的瞬变电磁响应最小，这一大小关系与不同激励能量间的关系是完全吻合的，见式（18），也就是说，激励能量大对应的响应就大。因此如果只想了解哪个激励波形所产生的响应大，就不需要依次对响应大小进行计算，而只需计算它们的激励能量大小。而在on－time段，当t＝0.01μs时，方波的响应最大，为7.096×107nV，在0.06ms至1.24ms梯形波的响应最大，为7.471×105nV，在1.24ms到3.75ms三角波响应最大，为3.767×105nV，而从3.75ms至完全关断时刻t＝5ms之间，响应的最大值变为梯形波最大，为7.46×105nV，因此激励能量与瞬变电磁响应间的大小关系只适用于off－time段。

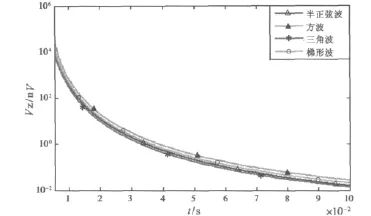
图4 四种波形完全关断后的三层大地瞬变电磁响应

3 三层大地地－空瞬变电磁响应分析

以三层大地为模型，将地－空瞬变电磁响应分为on－time段和off－time段进行分析。根据电导率值的不同分为高阻模型、低阻模型和均匀半空间模型进行计算，除电导率外其余参数均与图4所取参数相同，电导率参数见表3.

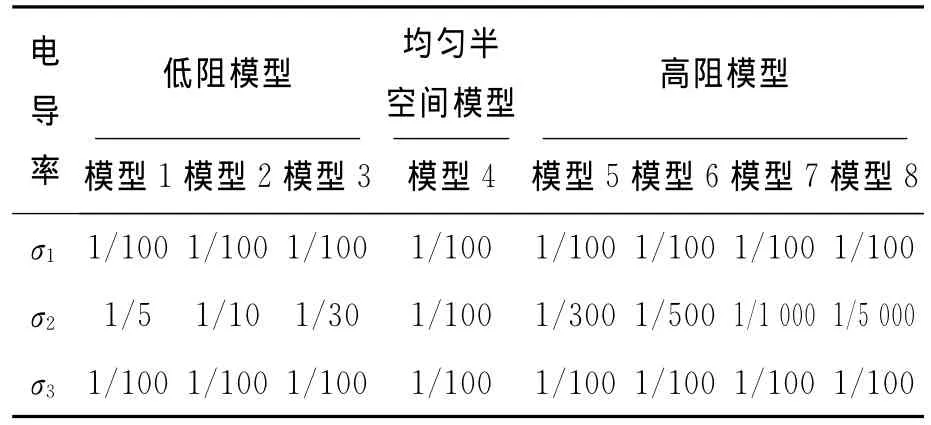
表3 不同模型电导率值

图5～图8分别为半正弦波、方波、三角波和梯形波的on－time与off－time段电磁响应。分析并得出如下结论：

1）在on－time段，无论是低阻模型还是高阻模型，半正弦波与三角波的响应无明显变化。而对于方波和梯形波，低阻模型响应变化明显。在关断早期，也就是（0.005s，0.005 3s）之间，高阻模型与低阻模型的响应混叠在一起，不利于进一步的反演。

2）分析图6和8，地－空电磁探测系统的响应在off－time段，高阻模型比低阻模型衰减的快，如果只记录off－time段响应，当中间层电导率逐渐减小时，对于实测数据而言，高阻异常很快进入噪声区，因此无法得到足够多的高阻段有用信息。解决的办法是发射波形采用梯形波或方波，接收机同时记录off－time和on－time段的响应。

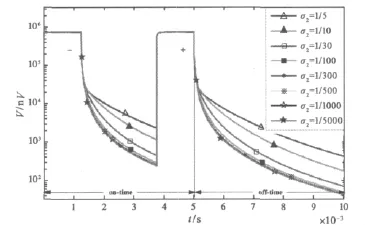
图8 梯形波激励on－time与off－time段对不同电导率的电磁响应

3）半正弦波和三角波在on－time段的响应随电导率的变化不明显。在t＝3.3ms时刻，半正弦波以均匀半空间模型计算的响应结果为比较基准，高阻模型和低阻模型的平均响应幅值差比仅为0.823%，三角波为0.839%，而方波和梯形波分别为139.41%和135.17%.因此，采用方波和梯形波激励时，记录on－time段和off－time段数据进行异常分析，可使反演分辨率更高。

4 结 论

以阶跃波层状大地地－空瞬变电磁响应为基础，利用卷积方法计算了方波、梯形波、半正弦波和三角波的on－time和off－time段地－空瞬变电磁响应。通过这一方法可用来计算任意激励波形的瞬变电磁响应。同时研究了激励能量对瞬变电磁响应大小的影响：激励能量越大对应的off－time段响应越大。为了较好完成高阻异常的解释处理，最好采用方波和梯形波作为激励信号，由于高阻异常很快进入噪声区，因此接收机不仅要记录off－time段数据同时还要记录on－time段数据以得到足够多的数据完成后期的解释处理。

［1］Canada Tungsten Mining Corporation.Report on a Combined TURAIR Electromagnetic and Magnetic Survey［R］.MAYO：Mining Recorder Land Agent，1975.

［2］MOGI T，YOSHIKAZU T，KEN＇ICHIROU K，et al.Development of grounded electrical source airborne transient EM （GREATEM）［J］.Exploration Geophysics，1998，29（2）：61－64.

［3］TORU M，KEN＇ICHIROU K，HIDESHI K，et al.Grounded electrical－source airborne transient electromagnetic （GREATEM）survey of Mount Bandai，north－eastern Japan［J］.Exploration Geophysics，2009，40（1）：1－7.

［4］SMITH R S，ANNAN A P，MCGOWANA P D.A Comparison of data from airborne，semi－airborne，and ground electromagnetic systems［J］.Geophysics，2001，66（5）：1379－1385.

［5］ELLIOTT P.The principles and practice of FLAIRTEM［J］.Exploration Geophysics，1998，29（2）：58－60.

［6］LIU G M.Effect of transmitter current waveform on airborne TEM response［J］.Exploration Geophysics，1998，29（2）：35－41.

［7］于生宝，王 忠，嵇艳鞠，等.瞬变电磁法浅层探测技术［J］.电波科学学报，2006，21（2）：284－287.YU Shengbao，WANG Zhong，JI Yanju，et al.Time domain transient electromagnetic shallow prospecting［J］.Chinese Journal of Radio Science，2006，21（2）：284－287.（in Chinese）

［8］嵇艳鞠，林 君，王 忠，等.浅层瞬变电磁法中全程瞬变场的畸变研究［J］.电波科学学报，2007，22（2）：316－320.JI Yanju，LIN Jun，WANG Zhong，et al.Analysis of distortion in all－time transient electromagnetic field based on inducing of ramp switch－off current for shallow survey［J］.Chinese Journal of Radio Science，2007，22（2）：316－320.（in Chinese）

［9］许洋铖，林 君，嵇艳鞠，等.航空时间域电磁法回线源有限差分初始场计算［J］.电波科学学报，2010，25（2）：259－264.XU Yangcheng，LIN Jun，JI Yanju，et al.Calculation of initial field for loop source in airborne time－domain electromagnetic by finite－difference approach［J］.Chinese Journal of Radio Science，2010，25（2）：259－264.（in Chinese）

［10］YIN C C，SMITH R S，HODGES G，et al.Modeling results of on－and off－time B and dB／dt for timedomain airborne EM systems［C］／／70th EAGE Conference ＆ Exhibition－Rome，Roma，Italy，9－12June 2008.

［11］米萨克N纳比吉安.勘查地球物理－电磁法［M］.北京：地质出版社，1992：217－231.

［12］GUPTASARMA D，SINGH B.New digital linear filters for Hankel J0and J1transforms［J］.Geophysical Prospecting，1997，45（5）：745－762.

［13］GUPTASARMA D.Computation of the time－domain response of a polarizable ground［J］.Geophysics，1982，47（11）：953－963.

［14］NABIGHIAN M N，ORISTAGLIO M L.On the approximation of finite loop sources by two dimensional line sources［J］.Geophysics，1984，49（7）：1027－1029.