宜万铁路狮子口大桥车桥耦合振动仿真分析
韩 威,杨永清,余华丽,晋智斌
(西南交通大学土木工程学院,四川成都 610031)
列车通过桥梁时将会引起桥梁结构的振动,而桥梁结构的振动反过来影响列车的振动,这种相互作用、相互影响的问题就是列车与桥梁之间耦合振动的问题。一般运用桥梁结构动力学与车辆动力学结合的研究方法,将车—桥作为联合动力体系,建立车—桥耦合振动分析模型,以轨道不平顺或人工蛇形波作为系统的激励源,对列车以不同速度通过桥梁时的空间耦合振动响应进行研究[1]。
传统铁路桥梁的设计方法是通过动力系数来考虑列车过桥时对桥梁的动力作用。普通线路上的列车运行速度尚未达到桥梁的共振速度,而客运专线的设计时速为200~350 km/h,此速度范围可能已经进入桥梁结构共振的速度范围[2]。在共振条件下,桥梁动力响应按传统的动力系数考虑是明显不合适的。列车速度的提高和荷载的加大,使得车、桥之间的动力作用放大,动力指标很可能成为设计的控制要素[3]。
合理的桥梁竖向和横向刚度保证列车在过桥时有足够的抗脱轨安全度,满足列车通过时的平稳性及旅客和司机的舒适度要求。而高速铁路对运营安全性和舒适性都提出了更高的要求,因此对客运专线桥梁的设计和既有线提速时桥梁的安全性评估,进行车桥耦合振动研究具有重大意义。
本文采用有限元程序建立动力分析模型,计算列车以不同速度匀速通过该桥时车桥系统的空间振动响应。根据桥梁结构自振特性以及车—桥耦合振动分析结果从脱轨系数、平稳性指标等方面对列车运行的安全性和舒适性进行评判。
1 结构设计及其自振特性
宜万铁路是我国“八纵八横”铁路网主骨架之一,是沿江铁路通道的重要组成部分。狮子口大桥是宜万铁路的重要工程,主桥采用(48+80+48)m三跨变截面连续梁结构,中间2#,3#墩高分别为71 m,72 m。梁体截面为单箱单室,箱底外宽5.70 m,中支点处梁高5.90 m,端部及跨中处梁高 3.30 m。桥面总宽10.70 m,道碴槽宽8.40 m,两侧人行道各1.15 m,按双线Ⅰ级铁路设计,总体布置图见图1。

图1 主桥总体布置(单位:cm)
采用空间杆系有限元法,对桥梁结构进行离散,墩、梁均采用空间梁单元模拟,根据建立的全桥结构计算模型,计算桥梁的自振特性。其中前10阶自振频率及相应振型的计算结果见表1。桥梁结构的一阶横向弯曲振型对应的频率为0.781 Hz,一阶垂向弯曲振型对应的频率为1.598 Hz,自编程序与ANSYS计算结果误差较小(≤0.4%),振型相同。
2 车—桥耦合振动计算条件及评价标准
2.1 轨道不平顺
我国干线轨道谱与美国六级谱相当[4-6],因此轨道不平顺采用美国六级谱。

表1 自振频率及振型特点
2.2 列车编组及计算时速
计算时,采用的列车编组为“1节SS8机车+19普通客车”。计算行车速度包括 80,100,120,140,160 km/h,每一级速度分列车单线行车和双线对开2项。
2.3 车—桥响应评价标准
列车通过时,在车辆荷载及轨道不平顺的作用下,车辆和桥梁的振动被激发起来,过大的桥梁和车辆振动会影响行车安全性和乘坐舒适度。为保证车辆运行的安全性、舒适度,以及桥梁的使用性能,车辆及桥梁的动力响应要满足相应的标准。
桥梁结构一般根据梁端转角,梁体横、竖向振幅及加速度对桥梁动力性能进行评价。国内外研究者大多采用脱轨系数、轮重减载率来评判列车运行安全性,用Sperling指标来判断乘坐舒适性。轮轨垂向力较小时,轮轨蠕滑系数也小,此时的轮轨横向力不大,脱轨系数采用两个较小数值的比值。测量误差对脱轨系数的影响较大,不宜单独采用脱轨系数对车辆运行安全性做出评判,一般结合轮重减载率综合评判。在本研究中,将列车行车安全性与舒适性评价指标取为:梁端转角≤2‰,脱轨系数≤0.8,轮重减载率≤0.6,轮轨横向摇摆力≤80 kN,车体竖向加速度<1.3 m/s2(半峰值),车体横向加速度<1.0 m/s2(半峰值)。Sperling舒适度指标<2.50为优良,2.50~2.75为良好,2.75~3.00之间为合格,>3.00为不合格[7]。
3 车—桥耦合振动分析
3.1 挠度动力系数
各行车工况下,各跨跨中的挠度动力系数计算结果与列车运行速度的关系见图2。曲线大致呈现随速度增大而增大的规律,左、右侧边跨跨中挠度动力系数普遍比中跨跨中大。在行车速度为160 km/h时,左跨跨中挠度动力系数达到最大值1.095,根据规范所给动力系数计算公式计算结果为1.087,两者结果相差不大[8-9]。

图2 挠度动力系数计算结果
3.2 梁端转角
行车速度对梁端转角的变化影响不大。单线行车的最大梁端转角为0.371‰,双线行车的最大梁端转角为0.424‰,均小于限值2‰。梁端转角计算值较小,与行车速度关系不明显,同一行车速度下,双线行车普遍较单线行车大,与一般实测结果一致。
3.3 桥梁动力响应
桥梁的动力响应部分数据结果见表2,分析可见:随列车运行速度提高,桥梁各跨跨中的横、竖向动位移、加速度均呈单调增大的趋势。中跨跨中竖向动位移最大值为14.13 mm,相应的竖向挠跨比为1/5 662;横向动位移最大值为1.19 mm,相应的横向挠跨比为1/67 230;最大竖向和横向加速度分别为0.63 m/s2和0.42 m/s2。上述指标均表明,狮子口大桥具有足够的横向、竖向刚度,振动状态良好。
3.4 车辆动力响应
车辆的动力响应分析结果如下:
1)随列车运行速度提高,列车的安全性指标——脱轨系数、轮重减载率、横向摇摆力、车辆的加速度和舒适性指标均呈单调增大的趋势。
2)列车行车速度为100 km/h时的轮轨垂向力时程曲线见图3,根据曲线可以求得脱轨系数及轮重减载率。机车和车辆的脱轨系数、轮重减载率最大值分别为0.34,0.25,0.39和0.22,满足本文所采用指标:脱轨系数≤0.8,轮重减载率≤0.6。说明列车满足行车安全性的要求。
3)机车和车辆竖向加速度最大值分别为1.50 m/s2和1.04 m/s2,横向加速度最大值分别为1.85 m/s2和0.88 m/s2,竖向加速度和横向加速度分别小于1.3 m/s2和1.0 m/s2的限值。Sperling平稳性指标,除160 km/h时机车为“良好”外,其余均为“优良”。
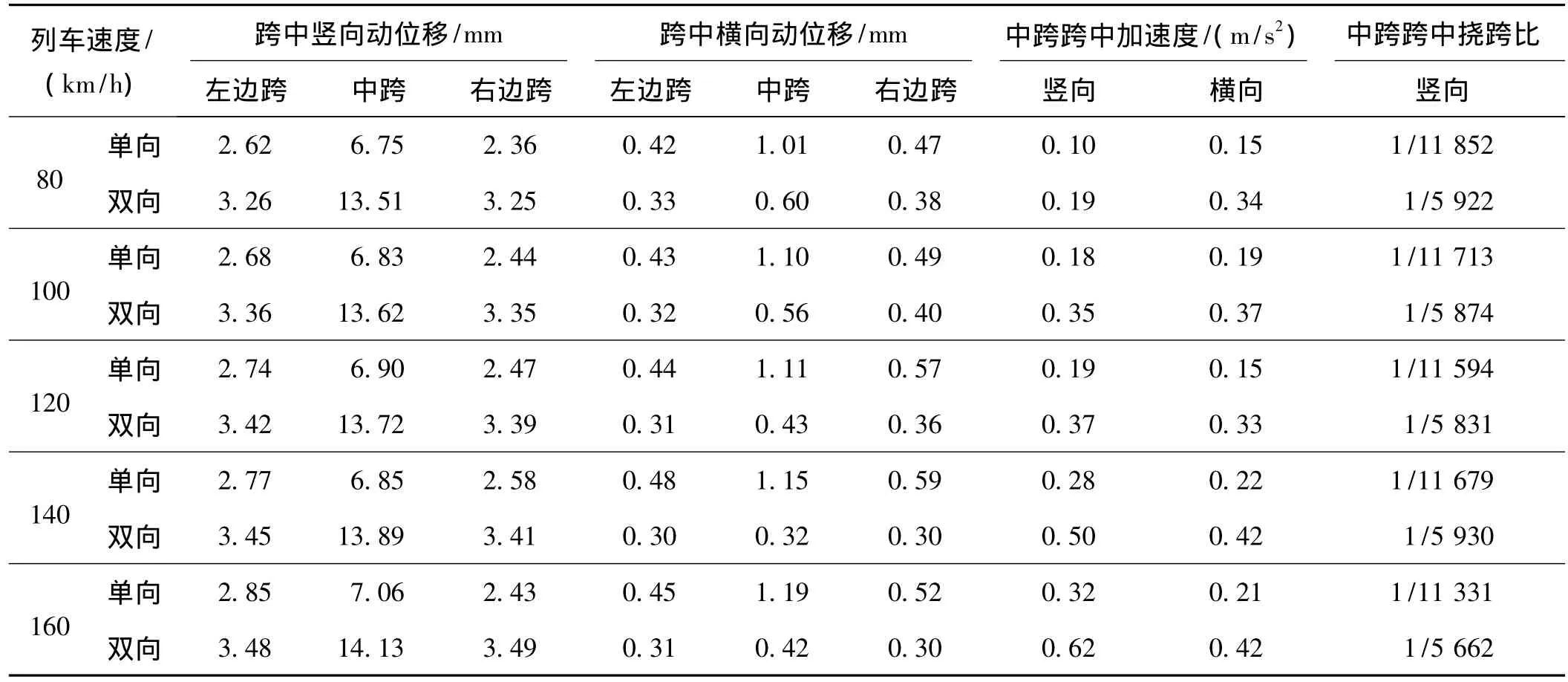
表2 桥梁结构动力响应
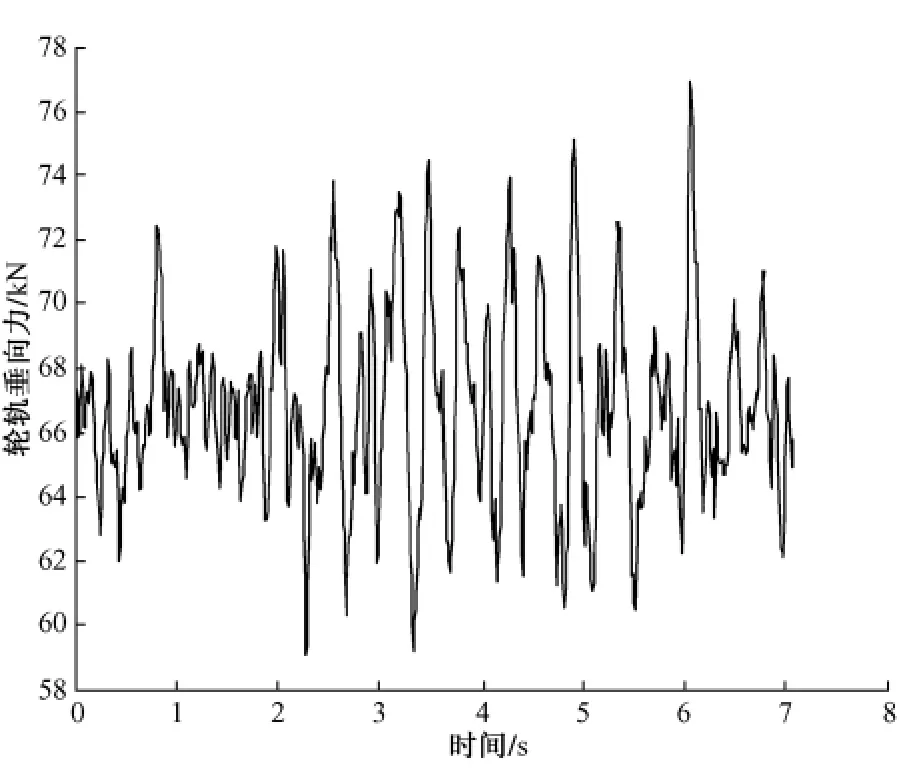
图3 轮轨垂向作用力时程曲线
4 结论
采用有限元方法,对宜万铁路狮子口连续梁桥耦合振动响应进行了仿真分析,得到以下结论:
1)桥梁结构的一阶横向弯曲振型对应的频率为0.781 Hz,一阶垂向弯曲振型对应的频率为1.598 Hz,狮子口大桥的整体横向及竖向刚度较好。在美国六级不平顺谱的前提下,列车对桥梁结构的冲击与规范计算差别不大。
2)梁体横向振幅、竖向振幅和加速度以及梁端转角计算值均处于合理范围,满足要求,也表明结构的横向、竖向刚度较好,振动状态良好。
3)机车和车辆的各项动力学指标均随列车运行速度提高而单调增大。机车和车辆的脱轨系数、轮重减载率、横向竖向加速度均满足要求。横向、竖向Sperling舒适性指标,除160 km/h时机车为“良好”外,其余均为“优良”。列车在设计时速下可以安全通过大桥,机车和车辆的运行安全性和舒适性都具有一定的储备,满足设计要求。
[1]秦顺全.宜万铁路万州长江大桥设计与施工[J].铁道工程学报,2006,92(2):20-23.
[2]GOICOLEA J M,DOMFNGUEZ J,NAVARRO J A,et al.New dynamic analysis methods for railway bridges incodes IAPF and eurocod [J].Railway Bridges Design,Construction and Maintenance.Spanish Group of IABSE Madrid,2002:12-14.
[3]晋智斌.车—线—桥耦合系统及车—桥随机振动[D].成都:西南交通大学,2007.
[4]CHU K H,GARG V K,WANG T L.Impact in railway prestressed concrete bridge[J].Journal of Structural Engineering,ASCE.1986,112(5):1036-1051.
[5]陈果.车辆—轨道耦合系统随机振动分析[D].成都:西南交通大学,2000.
[6]蔡成标,翟婉明,王开云.高速列车与桥上板式轨道动力学仿真分析[J].中国铁道科学,2004,25(5):57-60.
[7]中华人民共和国铁道部.铁建设函[2005]285号 新建时速200公里客货共线铁路设计暂行规定[S].北京:中国铁道出版社,2004.
[8]王贵春,潘家英,刘文武.铁路桥梁与车辆动力相互作用的协调条件分析[J].铁道建筑,2006(12):1-3.
[9]王贵春,章长玖,陈淮.公路简支梁桥在车桥耦合作用下的冲击系数研究[J].铁道建筑,2011(9):20-23.

