无界域上一类半线性波动方程的全离散谱格式

黄 瑜，徐承龙

（1.同济大学 数学系，上海200092；2.南京信息工程大学 数理学院，江苏 南京210044；3.上海市科学计算E－研究院及上海市科学计算重点实验室，上海200234）

近年来无界或半无界区域上的谱方法越来越受到广大的关注.这主要是因为谱方法的高精度和无需强加人工边界条件等优点.对于无界区域上的问题，Guo和 Xu［1］考虑了权函数为e－x2的 Hermite多项式作为基函数的逼近问题.其他还有很多关于将Hermite多项式作为基函数作逼近的文献［2－3］，但其中大部分的权函数都是非一致的，从而会加大在理论分析和数值实现过程的复杂性.因此一些学者考虑采用 Hermite函数作为基函数来逼近［4－5］.

本文主要讨论无界域上的带强阻尼项的半线性波动方程

其中未知函数u＝u（x，t），而g（x，u）是给定的一类关于x和u的非线性函数，例如形如ua的幂函数，g满足的非线性假设条件将在下文中给出.问题的初始条件为

带有阻尼项的波动方程弱解的存在性已经有很多文献讨论过［6－9］，但是关于这类波动方程的数值解却研究得较少.Macías－Díaz和 Puri［10］给出了有界域上的一类带有弱阻尼项的波动方程的有限差分格式.Gülle［11］对一类强耗散波动方程建立了关于时间的周期问题的三层差分格式，其收敛速度是O（Δx2＋Δt2）.

对于问题（1），（2），笔者采用一类新的 Hermite函数，即 Hermite多项式乘上e－x2／2，作为基函数来逼近.由于随着多项式项数N的增加，Hermite多项式的零点分布在整个无穷区域上，从而不需要再截断成有界区域计算.文献［12］成功运用这种方法研究了Dirac方程的数值解.由于方程（1）中强阻尼项Δut以及非线性项的出现，相应理论分析及数值计算更难于处理.

1 Hermite函数的性质和逼近结果

为了方便起见，记Sobolev空间L2（R），Lp（R），L∞（R）和Hr（R）相应的范数分别为‖·‖，‖·‖Lp，‖·‖∞和‖·‖r.L2（R）与Hr（R）上的内积记为（u，v）和（u，v）r.｜·｜r表示Hr（R）上的半范.

记Hl（x）为l次 Hermite多项式，定义l次Hermite函数为

易知其满足如下的递归关系［12］：

由Hermite多项式的正交性可知｛（x）｝在L2（R）上正交

且

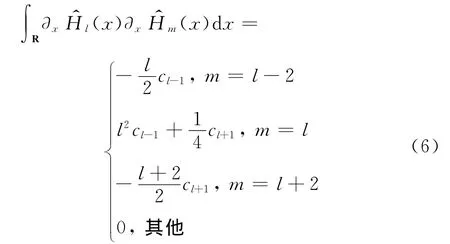
设N为任意的正整数，PN为不超过N次的代数多项式集合.HN＝span｛（x），（x），…（x）｝，常数c与任意函数以及N无关.

引理1［12］对任意的φ∈HN，1≤p≤q≤∞，m为任意的非负整数

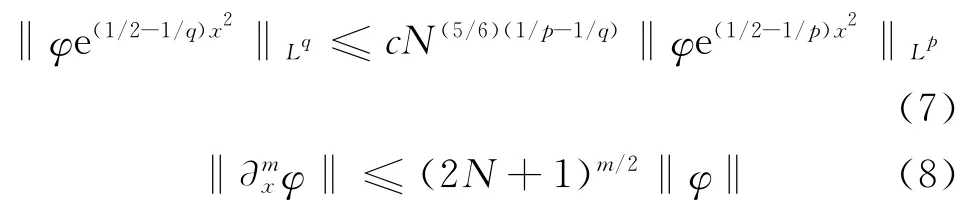
定义2个正交投影算子，L2（R）正交投影PN：L2（R）→HN为对任意的v∈L2（R），满足

H1（R）正交投影P1N：H1（R）→HN为对任意的v∈H1（R），满足

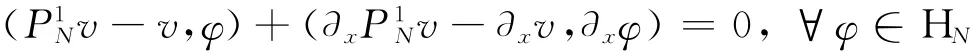
为给出投影算子的误差，定义算子A：Av（x）＝∂xv（x）＋xv（x）.对任意的非负整数m，定义空间（R）为（R）＝｛v｜v在R上可测，且‖v‖m，A＜∞｝，其相应的范数‖v‖m，A＝‖Amv‖.对任意正实数r，空间（R）由空间插值定义得到.因此可以得到如下投影算子的逼近性质.

引理2［12］对任意的v∈（R），0≤μ≤r，有‖PNv－v‖μ≤cN（μ－r）／2‖v‖r，A.

定理1 对任意的v∈HrA（R），r≥1

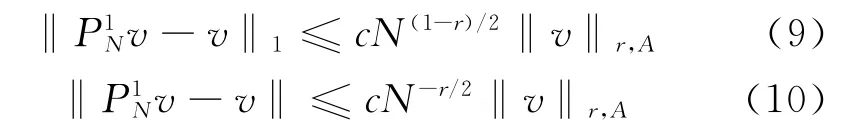
证明 由投影定理和引理2，得

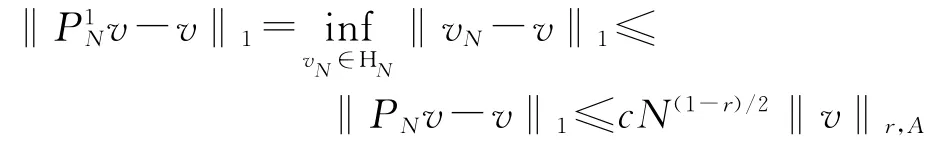
设g∈L2（R），若

由Lax－Milgram定理可知式（11）存在惟一的解，且‖w‖2≤c‖g‖.在式（11）中取z＝v－，可得

因此

则有

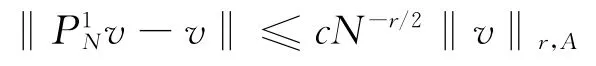
定理2 对任意的v∈（R），0≤μ≤r

证明 只需证明μ为非负整数的情况，其他情况则可由空间插值得到.下面用归纳法证明.由定理1可知，当μ＝0时结论成立.假设

则由引理1知对任意的整数μ≥1，有

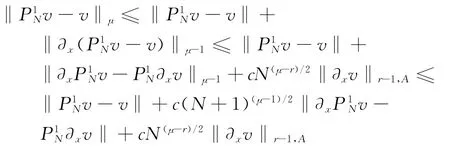
由定理1及

有

推论1 对任意的v∈（R），正实数r＞1／2，‖‖∞≤c‖v‖r，A.

设问题（1），（2）中的非线性项g（x，z）：R2→R上局部有界和可测的，对于任意的x∈R，g（x，·）∈C2（R）且存在正常数cj，j＝1，…，4，α∈［1，3］，及p，r0＞0使得对所有的x∈R一致成立；

若条件（A1）—（A5）满足，则对每个u0∈H1（R），w0∈L2（R），f∈L2（0，T；H－1（R）），问题（1），（2）对于任意的T＞0，在区间［0，T］上具有惟一的弱解u∈C（0，T；H1（R）），ut∈C（0，T；L2（R））∩L2（0，T；H1（R）），utt∈L2（0，T；H－1（R））＋L1（0，T；L2（R））［6］.

2 全离散格式

为了建立全离散格式，首先考虑问题（1），（2）的弱形式：寻找u∈C（0，T；H1（R）），ut∈C（0，T；L2（R））∩L2（0，T；H1（R）），utt∈L2（0，T；H－1（R））＋L1（0，T；L2（R）），使得对任意的ξ∈H1（R）有

其中u0∈H1（R），w0∈L2（R），f∈L2（0，T；H－1（R））.

运用 Hermite谱方法求解问题 （1），（2）.设τ为时间步长，T＝nTτ，Rτ（T）＝｛t＝kτ｜k＝1，2，…，记

问题（1），（2）的全离散格式为：寻找uN∈HN，使得对于任意的Ψ∈HN，有

于是在每个时间层上，需要求解下列方程：寻找uN（t＋τ）∈HN，使得对于任意的Ψ∈HN有下式成立：

其中xj是Hermite－Gauss点.

下面分析离散格式的收敛性和稳定性.首先证明格式（15）的收敛性，设UN＝.由式（14）可知，对任意的Ψ∈HN，当任意的t∈Rτ（T），有

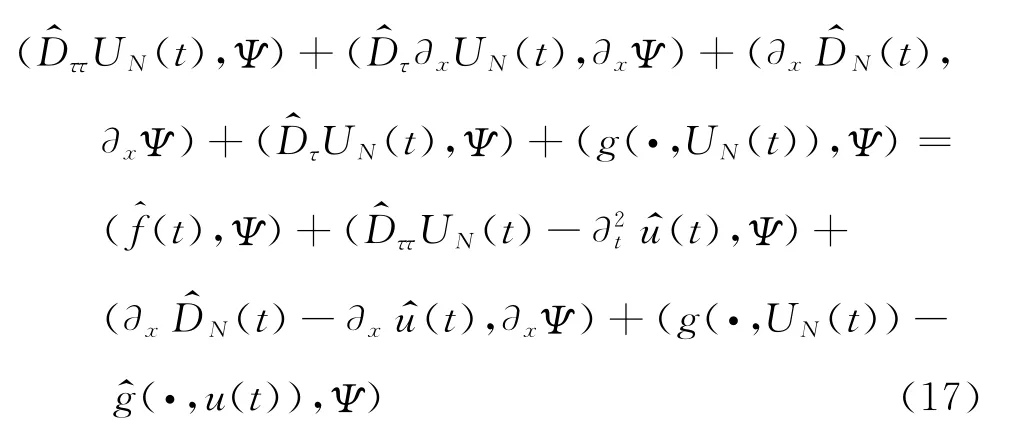
初值满足

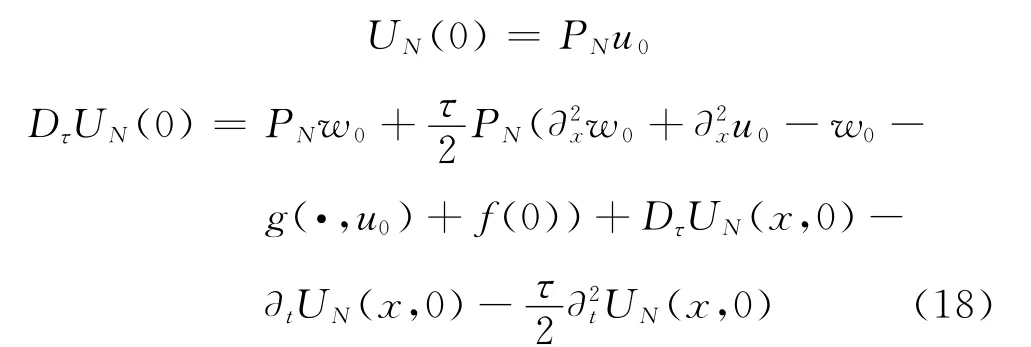
设＝uN－UN，式（15）减去（17），得

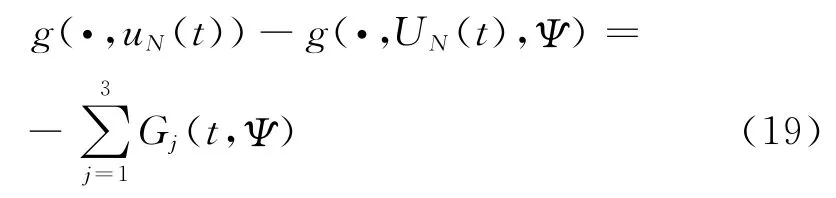
其中

初值满足

对任意的s∈Rτ（t－τ），根据（A6），推论1，引理1和Cauchy－Schwarz不等式，对于r＞1／2，可得

其中C＊（u）是仅依赖于‖u‖L∞（0，T；HrA（R））的正常数.

由定理1和文献［13］中的引理4.6，可得

其中C1，…，C6是与N，τ无关的正常数，Cg＝

将式（21）对s∈Rτ（t－τ）求和，利用式（22）—（25）和Young不等式得到

其中C7，C8，C9是与N，τ无关的正常数.

其中ρ1（t）＝O（τ4＋N1－r）.

应用离散的Gronwall不等式（文献［14］中定理4），可得

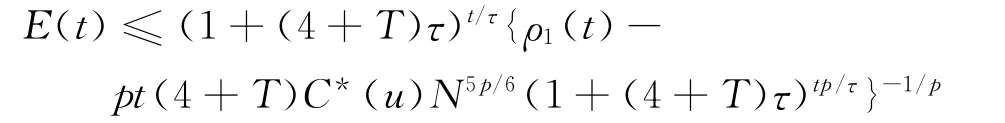
当r＞11／6时，若τ充分小，且满足τ4N5／6≤ε0，可得E（t）≤ρ1（t）.因此得到下面的收敛性结果.

定理3 设u（x，t）为问题（1），（2）的解，uN（x，t）为离散格式（15）的解，且u（x，t）满足u∈C2（0，T；HA（R））∩C（0，T；HA（R））∩H4（0，T；L2（R））∩H2（0，T；H1（R））∩H1（0，T；L4（R）），则当r＞11／6时，且满足τ4N5／6≤ε0时，对于t∈（T）

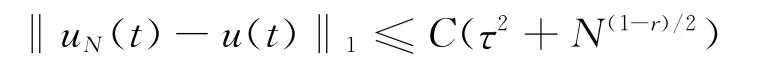
其中常数C只依赖于u，f，u0，w0.

下面证明离散格式（15）的稳定性.记分别为uN，f对应的误差，则由式（15），得

取（t），代入式（27），有

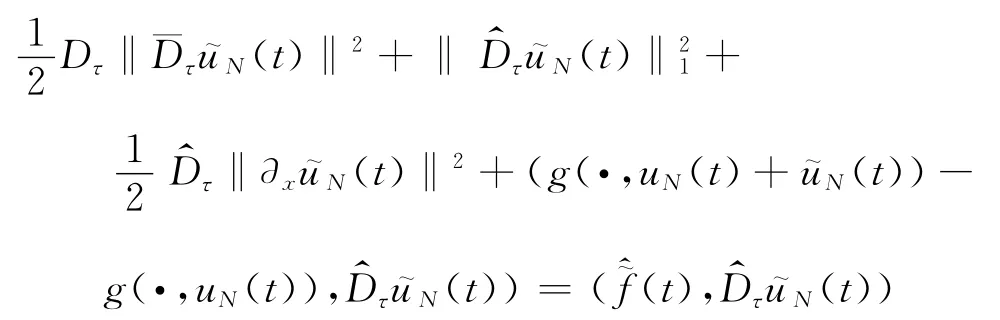
对s∈Rτ（t－τ）求和，对任意的x∈R，由g（x，·）∈C2（R）及Young不等式，与收敛性的证明过程类似，可得

其中C10，C11，C12是与N，τ无关的正常数.记

由文献［15］中的引理3.7，可得格式的稳定性结论.

定理4 设u（x，t）为问题（1），（2）的解，uN（x，t）为离散格式（15）的解，则当ρ2（t）充分小时，对于t∈¯Rτ（T），有

其中常数C，C′只依赖于uN.

3 数值算例

取非线性项g（x，u）＝（u（x，t））3，考虑问题（1），（2）的解析解为：u（x，t）＝e－x2cos（xt）.首先，取时间步长τ＝10－3，图1和图2分别描述了当t＝0.1和t＝1时的误差Er与多项式项数N之间的关系，‖uN（t）－u（t）‖～e－CN.为了考察误差与时间步长τ的关系，固定N＝126，图3描述了在t＝1时刻，L2误差与时间步长的关系，从数值结果可以看出‖uN（t）－u（t）‖～τ2.

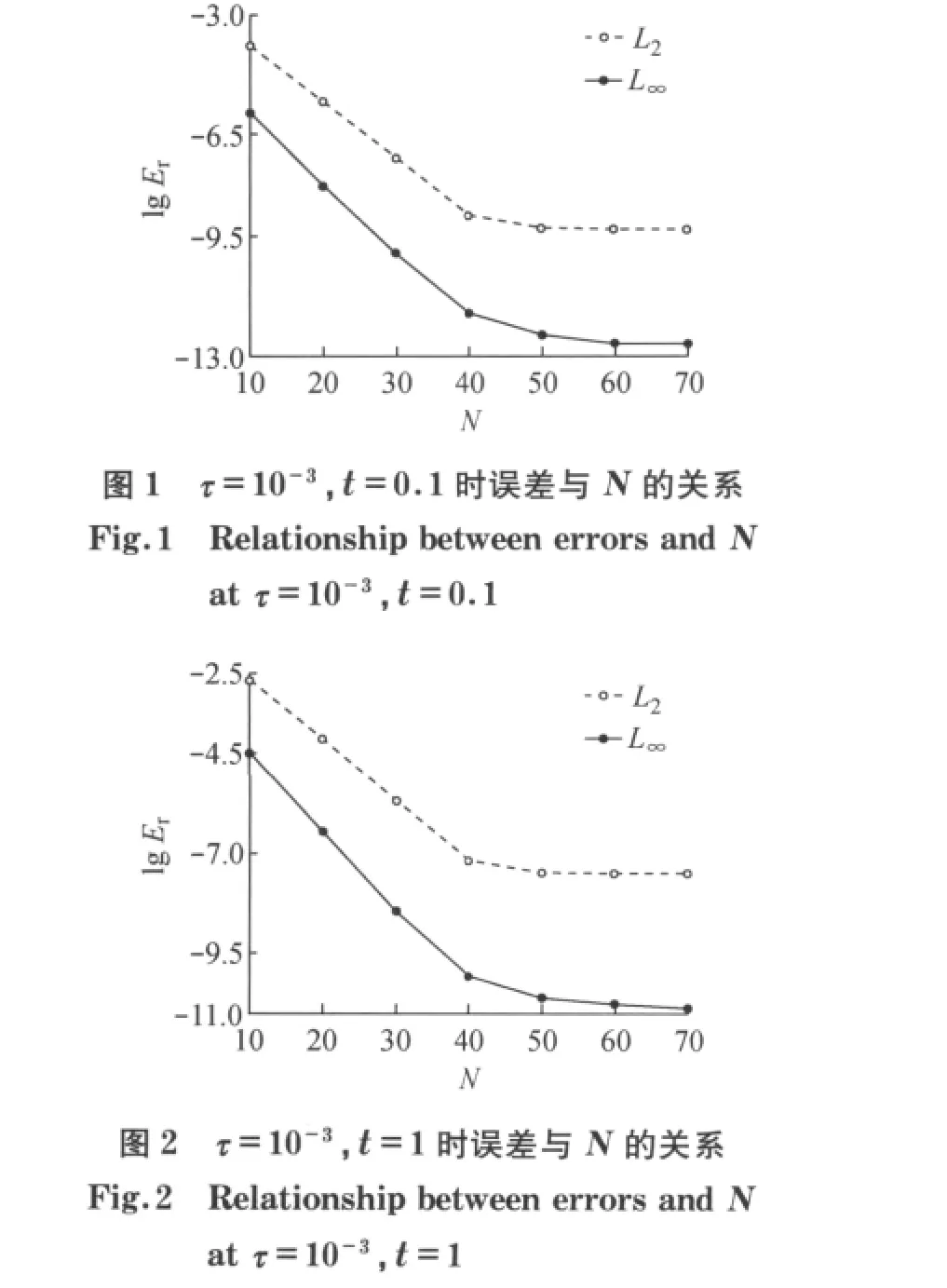
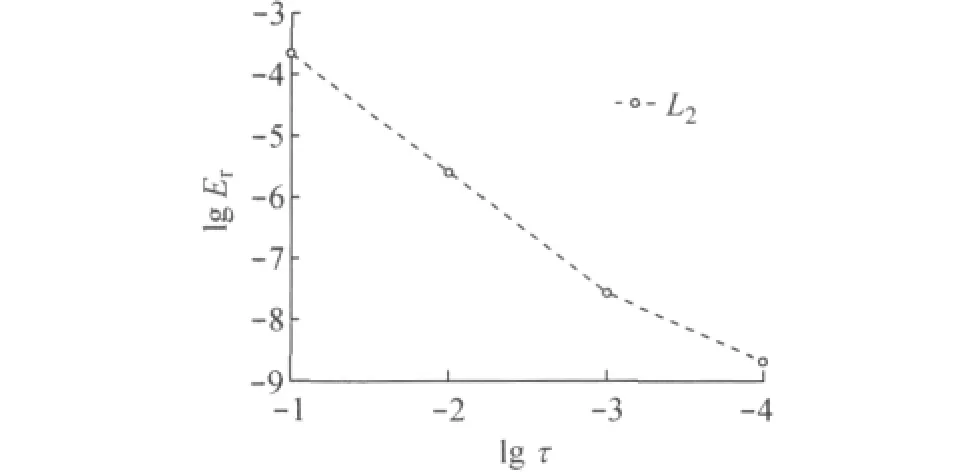
图3 N＝126，t＝1时误差与τ的关系Fig.3 Relationship between error andτat N＝126，t＝1

［1］Guo B Y，Xu C L.Hermite pseudospectral method for nonlinear partial differential equations［J］.Mathematical Modelling and Numerical Analysis，2000，34（4）：859.

［2］Guo B Y.Error estimation for Hermite spectral method for nonlinear partial differential equations［J］.Mathematics of Computation，1999，68（227）：1067.

［3］Xu C L，Guo B Y.Hermite spectral and pseudospectral methods for nonlinear partial equations in multiple dimensions［J］.Computational and Applied Mathematics，2003，22（2）：167.

［4］Funaro D，Kavian O.Approximation of some diffusion evolution equations in unbounded by Hermite functions［J］.Mathematics of Computation，1991，57（196）：597.

［5］Boyd J P.The rate of convergence of Hermite functions series［J］.Mathematics of Computation，1980，35（152）：1309.

［6］Belleri V，Pata V.Attractors for semilinear strongly damped wave equations onR3［J］.Discrete and Continuous Dynamical Systems，2001，7（4）：719.

［7］Carvalho A N，Cholewa J W，Dlotko T.Strongly damped wave problems：bootstrapping and regularity of solutions ［J］.Journal of Differential Equations，2008，244（9）：2310.

［8］Ikehata R.Decay estimates of solutions for the wave equations with strong damping terms in unbounded domains［J］.Mathematical Methods in the Applied Sciences，2001，24（9）：659.

［9］Pata V.Attractors for a damped wave equation onR3with linear memory［J］.Mathematical Methods in the Applied Sciences，2000，23（7）：633.

［10］Macías－Díaz J E，Puri A.A boundedness－preserving finitedifference scheme for a damped nonlinear wave equation［J］.Applied numerical mathematics，2010，60（9）：934.

［11］Gülle A.On the numerical solution of quasilinear wave equation with strong dissipative term ［J］.Applied Mathematics and Mechanics，2004，151（2）：581.

［12］Guo B Y，Shen J，Xu C L.Spectral and pseudospectral approximations using Hermite functions：application to the Dirac equation［J］.Advances in Computational Mathematics，2003，19（1）：35.

［13］Guo B Y.Spectral Methods and Their Applications［M］.Singapore：World Scientific Publishing，1998.

［14］Willett D，Wong J S W.On the discrete analogues of some generalizations of Gronwall＇s inequality［J］.Monatshefte für Mathematik，1965，69（4）：362.

［15］Ma H P，Sun W W.Optimal error estimates of the Legendre－Petrov－Galerkin method for the Koreweg －De Vries equation［J］.SIAM Journal on Numerical Analysis，2001，39（4）：1380.