信号交叉口控制延误算法的适应性研究

沈旅欧，刘好德

（1.华南理工大学 土木与交通工程学院，广东 广州510641；2.交通运输部科学研究院 城市交通研究中心，北京100029；3.同济大学 测量与国土信息工程系，上海200092）

控制延误是美国道路通行能力手册Highway Capacity Manual 2000版［1］（HCM 2000）中信号交叉口服务水平评价的主要指标.其普遍地被信号交叉口评价及配时软件接受为延误的标准表达形式.信号交叉口配时设计的主要目的之一就是通过优化设计来减少总控制延误.在HCM 2000中控制延误的计算采用的是改进的 Webster公式［2］.此公式包括3项延误：标准延误，增量延误和初始排队延误.

HCM 2000采用的是基于车道组的控制延误计算方式.通常将所有左转车道、直行车道或右转车道分别划归为一个车道组.而实际中同一车道组内各个车道的使用普遍存在不均衡的情况.这可能是由于驾驶员的车道选择习惯不同，各车道通行能力不同，或是驾驶员根据出行路径的需要而提前选择车道所造成.在车道不均衡使用的情况下，HCM 2000采用车道使用折算系数来对车道组的饱和流量进行修正.

笔者在一些信号配时设计的应用实践中常常遇到车道使用不均衡的情况.特别是在邻近高速公路立交匝道区域的信号交叉口，因为交叉口间距短，驾驶员需考虑在下一个交叉口的转向进入不同行驶方向的匝道，而造成车道的不均衡使用.对于车道使用不均衡的现象，美国科学院交通研究委员会（TRB）进行了实地数据收集研究，并在美国国家合作公路研究项目报告（NCHRP Report 599）中提出了在立交匝道交接交叉口的车道折算系数的默认值［3］.其中，对于4车道的情况最小的默认值低至0.289.笔者比较分析了在非饱和情况下控制延误分别采用HCM 2000基于车道组的控制延误计算方法和基于车道的控制延误计算方法，发现两者存在差异，进而对Webster延误公式进行了探析.据此推荐在非饱和情况下相对HCM 2000基于车道组的控制延误计算方法适应性更好的基于车道的控制延误计算方法.本文以下部分将从HCM 2000方法介绍与文献综述入手，通过实例比较分析，探析Webster延误计算公式，进而得出结论并提出相应的建议.

1 HCM2000方法及相关文献综述

在HCM 2000中控制延误是基于车道组计算的.在应用HCM 2000控制延误计算公式之前，车道组流量需经过高峰小时系数修正；而饱和流量则经过车道数，车道宽，重车百分比，坡度，路边停车，公交站台，区域类型，车道使用折算系数，左转车影响系数，右转车影响系数，行人对左转车的影响系数，以及行人与自行车对右转车的影响系数等的修正.

在实际情况中一个车道组内部各车道的饱和流量存在差异，特别是对于合用车道时，其饱和流量往往随实际分配不同行驶方向的车流量而动态变化.目前已有很多关于当同一车道组内各车道饱和流量不同时驾驶员如何选择行驶车道的研究.其研究结果也被不同的交通管理部门采用并实施于计算交叉口延误的软件中.澳大利亚的交叉口配时软件SIDRA采用的是均衡饱和度方法［4］；HCM 2000采用的是均衡流量比方法.这两种方法在同一车道组内各车道获得的有效绿灯时间一致时是等价的.同样瑞典［5］和加拿大［6］的通行能力手册也是采用均衡流量比的方法.但是与HCM 2000应用在车道组层面不同，SIDRA，瑞典和加拿大的方法是应用在各个车道的层面.当实地测量到车道使用不均衡时，HCM 2000中采用车道折算系数进行修正而计算车道组的控制延误.可以证明此方法实际上是隐性的使用了均衡流量比的方法，即假设流量在不同的车道当中是按照均衡流量比的方法分配的.除了均衡饱和度和均衡流量比两种车道流量分配的方法外，还有均衡排队长度方法，均衡延误方法，和最小旅行时间方法等［7］.Brandon在2002年通过实地数据研究发现均衡排队长度或均衡周期平均排队方法更能准确描述驾驶员在实地的车道选择方式［8］.当然这些发现还需要更多的实际调查数据来核实.

鉴于Webster方法中标准延误项的计算是建立在三角形形状的排队累计图形的基础上的，2005年Dennis提出了增量排队累计（IQA）方法［9］.这种方法是一种更加广义的 Webster方法，类似于Robertson在TRANSYT中的仿真方法，其适用于普遍的排队累计情况，包括在同一周期内多次绿灯的情况.并且其在过饱和情况下的计算方式也跟HCM 2000方法兼容.同时Dennis也建议在Highway Capacity Manual 2010版［10］（HCM 2010）中采纳Brandon的均衡排队长度的车道选择方法，并且将其应用在车道的层面上.而最新的HCM 2010采纳的是Dennis提出的IQA方法［10］，但仍然是基于车道组的层面.

上面介绍的文献讨论了在各个车道饱和流量不一致的情况下，如何估计实际各个车道分配的流量，从而计算控制延误.而本文则重点讨论在已知车道流量分布的情况下应该如何计算控制延误.在许多情况下，如果同一车道组中各车道的使用存在比较大的差别时，一般在进行信号配时前会到现场收集数据，然后按照HCM 2000介绍的方法计算出车道折算系数而替代延误计算软件中的默认值.下面通过实例来分析在这种情况下HCM 2000基于车道组的方法与基于车道的延误计算方法的差异，并在此基础上提出解决方案的建议.

2 非饱和状况下交叉口控制延误计算实例比较分析

在非饱和的情况下，控制延误的计算只存在标准延误和增量延误，而不包括初始排队延误.本文选取广州市人民路／西堤二马路／沿江西路交叉口的南行方向为研究目标车道组.此交叉口为定时独立信号控制，南行方向为两右转车道，车辆右转后经过西堤二马路内侧车道驶向人民路高架桥南行，外侧车道则驶向人民路高架桥北行.

2.1 HCM2000控制延误计算方法的实例应用

HCM 2000中控制延误的计算公式为

式中：D为控制延误，s；D1为标准延误，s；D2为增量延误，s；PF为协调控制和控制器类型的连续通行因子，独立交叉口为1.0；C为周期长度，s；T为分析时间长度，默认值为0.25h；g为有效绿灯时间，s；X为流量通行能力比，X＝ν／c；ν为流量，辆·h－1；c为通行能力，辆·h－1；k为增量延误因子，依据于控制器的设置，对于定时控制或近饱和状态为0.5；I为上游过滤系数，对于独立交叉口为1.0.

本实例交叉口几何布局如图1所示.

图1 实例交叉口几何布局图Fig.1 Intersection geometry layout of the case study

本实例中流量为小汽车流量，无高峰小时折算.根据实测数据右转单车道饱和流量接近1 200辆·h－1（即饱和车头时距约为3s）.南向右转实测总流量650辆·h－1，内侧车道流量244辆·h－1，外侧车道流量为406辆·h－1.实测交叉口交通控制参数为：周期为133s，相位绿灯损失为4s，南向相位绿灯时间为72s，有效绿灯时间则为68s.

控制延误计算相关公式有

式中：FLU为车道折算系数；ν1，ν2分别为车道组中车道一、车道二流量，辆·h－1；s为饱和流量，辆·h－1；s′为折算饱和流量，辆·h－1.

基于公式（1）—（6），本实例交叉口的南行方向车流的延误计算结果如表1.

在表1中同时列出了基于车道组的南向右转车流控制延误的计算结果和按照均衡流量比进行分配的基于车道的控制延误.可以看出两种方法的计算结果在标准延误项D1上是一致的.但是，增量延误D2的计算结果却存在较大的差异，基于车道的计算结果要明显大于基于车道组的计算结果.

表1 HCM 2000控制延误计算结果Tab.1 Results of control delay calculation by HCM 2000

2.2 非均衡车道使用情况下两种计算方法的控制延误比较

上面按照HCM 2000基于车道组控制延误的计算方法计算了实例交叉口的延误.下面提出一种基于车道的控制延误计算方法.其前提假设与HCM 2000方法的前提假设不同，这里假设车道使用不均衡不是由于车道饱和流量不同造成的，而是由于驾驶员提前选择车道的原因而造成车道使用不均衡的现象.因此，各车道的通行能力是一样的.其计算结果如表2所示.

表2 非均衡车道使用情况下控制延误计算结果比较Tab.2 Comparison of control delay results under unequal lane utilization

由表2计算结果可知：由于标准延误和增量延误的计算所包含的参数（车道通行能力、车道饱和流量和流量比）不同，导致计算结果存在差异.此种假设车道通行能力相同情况下基于车道的方法计算得到的标准延误和总控制延误都要低于前面两种方法，增量延误则介于前面两种方法之间.

同时还发现，基于车道组的计算方法假设内外侧车道的控制延误相同，而按照HCM 2000均衡饱和流量比的流量分配方法计算得到的基于车道的控制延误则是内侧车道高于外侧车道，而表2中计算结果则是内侧车道延误低于外侧车道.从本实例可以看出计算方法的选用对控制延误计算结果有一定的影响.

为了明确在不同交通条件下对延误的计算结果的量化影响，本文对总流量、车道折算系数和饱和流量3个参数进行了关于HCM 2000基于车道组的方法及情况下基于车道的方法的敏感性分析，结果如表3所示.表中，情况1为ν＝650～950辆·h－1，s＝1 200辆·h－1，FLU＝0.8；情况2为ν＝650辆·h－1，s＝1 200辆·h－1，FLU＝0.6～0.9；情况3为ν＝950辆·h－1，s＝1 200～1 800辆·h－1，FLU＝0.8.

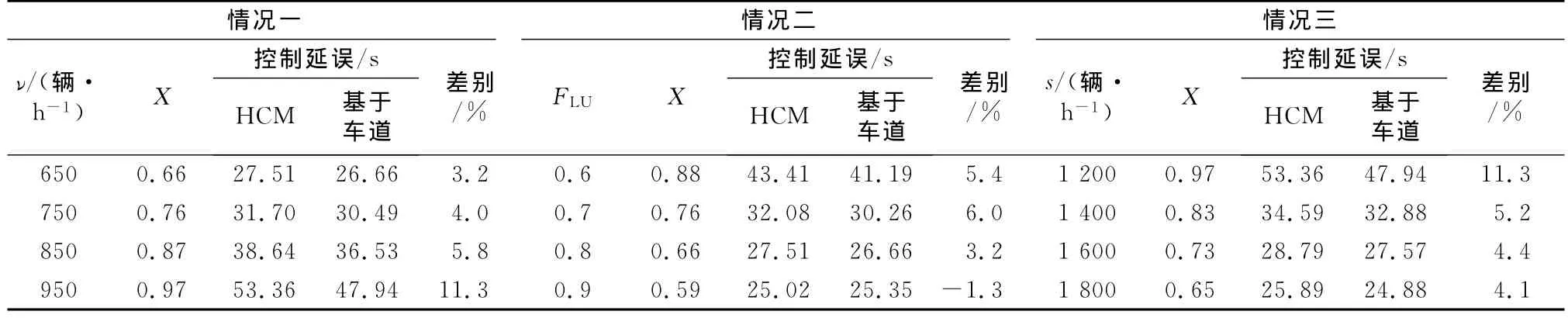
表3 控制延误计算敏感性分析Tab.3 Control delay calculation sensitivity analysis

从表3的敏感性分析可以看出，相对于本文提出的假设车道通行能力相同情况下基于车道的方法与HCM 2000基于车道组的方法存在－1.3%～11.3%的差异.且差异随着流量的增加，饱和流量的减少，即流量比的增加而增加；而相对于车道折算系数的变化则呈凸形曲线变化，在0.7左右达到最大，约为6.0%.这些进一步说明了两种方法的计算结果的差异是明显的.

同时，笔者还对实例交叉口进行了延误数据收集，结果如表4.

表4 实测控制延误Tab.4 Field measured control delay

对于本研究实例，实测延误均低于上面3种计算方法，而与给定各车道通行能力一样是基于车道的计算方法较接近.同时，实测结果也显示内侧车道的延误要低于外侧车道的延误.

对于两类控制延误的计算方法——基于车道组的方法和基于车道的方法，鉴于目前各国交通部门对他们的适用范畴没有明确的定义而导致存在不一样的实际应用范畴，造成使用者的概念混淆.因此，本文提出有必要对于这两种方法的使用范畴的命题进行分析.

3 Webster公式探析

原始Webster延误计算公式为

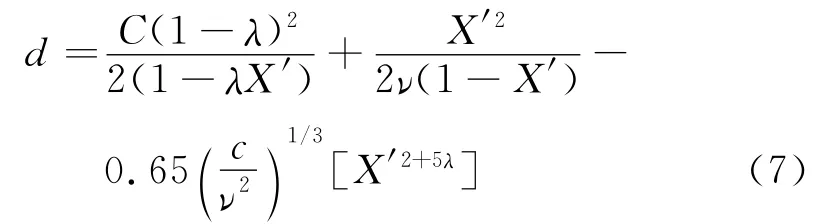
式中：d为平均总每车延误时间，s；λ为有效绿灯时间周期比，λ＝g／C；X′为饱和流量比，X′＝ν／cλ.

初始的Webster延误计算公式是从排队论M／D／1模型推导出来的.M表示泊松到达分布，D表示定长服务分布，1表示服务台.由于交叉口排队情况跟M／D／1模型存在差异，往往一个车道组包含多个车道，另外交叉口还有红灯时间的存在.而所有车辆在红灯期间到达都必须排队等候，因此 Webster根据均匀到达假设推导出了延误计算公式中的第1项即标准延误项.这个计算公式被大家所接受，且一直没什么变化.第2项则是根据M／D／1模型推导出来的.第3项为根据实测数据对总延误的一个经验修正项.Webster计算公式不适用于饱和度比较大（＞0.85）的情形，特别是当饱和度接近1时，延误趋于无穷大，这不符合实际.因此后来的HCM 2000中采用的是Kimber和Hollis在1979年提出的坐标变换的经验方法［10］对Webster模型进行修正后的公式，即式（3）.

因为车辆驶离交叉口的情况跟排队论的M／D／1有一个差别就是实际服务时间为零，所以计算交叉口延误采用的是M／D／1模型的平均排队时间，不是平均系统时间.M／D／1模型的概率论推导的排队延误计算公式如下：

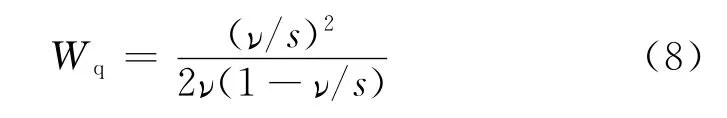
式中Wq为平均排队等候时间.

可以看出这个排队延误的计算公式与Webster公式中的第2项是一致的.但是实际交叉口1个车道组中往往存在2个或多个车道.当驾驶员能比较自由地根据不同车道的排队等候情况即通行能力情况而选择等候时间较少的车道时，其排队情形则与排队论中的M／D／C（C表示多服务台）相似.根据查阅的文献，目前对于M／D／C模型还没有确切的数学计算公式，往往采用的是一些近似计算公式.鉴于这些公式的推导和应用都非常复杂，也非本文的主旨.这里仅仅列出关于这个模型的一些定性的结论.由于在M／D／C模型中排队者可以先判断各服务台或车道的现状排队等候时间而自由地选择排队等候较少的服务台或车道通行.如果各车道流量比相同，由于多车道比单车道能较自由地选择车道，会较少地出现因为随机因素而导致短暂的到达流量超出饱和流量，因此其计算所得的平均等待时间或增量延误较小.

在使用基于车道的延误计算公式时，虽然流量比与基于车道组的情况相同，但是由于基于车道的公式中流量较基于车道组公式中的流量要小很多，且流量存在于公式（8）的分母，从而导致增量延误的计算结果偏大.

4 结论及建议

通过以上的实例分析及对Webster公式的探讨，笔者得出如下结论：当车辆可以在车道组内自由选择车道的情况下，应采用基于车道组的交叉口控制延误计算方法；当车辆在车道组内存在不均衡使用的情况，且此情况是由于驾驶员考虑到某些因素而提前做出车道选择所造成，即驾驶员的自由选择车道存在限制，而不是由于车道通行能力不同时，应采用基于车道的交叉口控制延误计算方法.

根据此结论，发现当存在驾驶员因为提前选择车道而导致车道不均衡使用的情况时，HCM 2000使用的车道折算系数的控制延误计算方法不能准确反映实际情况；同时，澳大利亚SIDRA采用的完全基于车道的控制延误计算方法在驾驶员能自由选择车道的情况下也不能准确反映实际情况.

对于采纳HCM 2000方法设计的信号交叉口配时软件，建议提供可由用户选择的基于车道的控制延误计算方法.这样在某些特殊情况下，特别是在进行立交附近交叉口的延误分析时，读者可以选择基于车道的控制延误计算方法进行分析以得到准确的结果.

［1］Transportation Research Board.Highway capacity manual［M］.Washington D C：Transportation Research Board，2000.

［2］Webster F V.Traffic signal settings ［R］.London：Road Research Laboratory，Her Majesty’s Stationery Office，1958.

［3］Transportation Research Board.Default values for highway capacity and level of service analyses［R］.Washington D C：Transportation Research Board，2008.

［4］Akcelik R，Besley M.SIDRA 5 user guide ［M］.Vermont South：Australian Road Research Ltd，1996.

［5］Hasson A.Swedish capacity manual［M］.Stockholm：National Swedish Road Administration，1977.

［6］Gough J W，Eng P.Canadian capacity guide for signalized intersections［M］.3rd ed.Toronto：Canadian Institute of Transportation Engineer，2008.

［7］Akcelik R.On the estimation of lane flows for intersection analysis ［R］.Vermont South：Australian Road Research Ltd，2001.

［8］Nevers B L，Rouphail N M.Field evaluation of lane selection strategies at signalized intersections ［J］.Journal of Transportation Engineering，2002，128（3）：224.

［9］Strong D W.New calculation method for existing and extended highway capacity manual delay estimation procedures［C／CD］∥ TRB85thAnnual Meeting Compendium of Papers CD－ROM，Washington D C：Transportation Research Board，2006：06－0106.

［10］McTrans Center.2010 Highway Capacity Manual（PDF）［EB／OL］.［2011－01－10］.http：／／mctrans.ce.ufl.edu／newsletters／10－January.pdf.

［11］Kimber R M，Hollis E M.Traffic queues and delays at road junctions［R］.Crowthorne：Transport and Road Research Laboratory，1979.