空气过滤器性能试验台喷嘴流量测量误差分析

林忠平，雷亚平

（同济大学 机械工程学院，上海200092）

随着现代工艺生产和科学实验活动的快速发展，空气过滤器在微电子、医疗、生物实验室等行业都需要达到较高的要求，同时对于常规办公与商场的民用建筑空调系统，也需要空气过滤器滤除空气中的尘埃，空气过滤器测试成为判定过滤器性能的依据.本文的空气过滤器性能测试实验台采用精确度高、测量范围广、测量简便的喷嘴组作为风量测量装置.目前关于喷嘴流量测量装置的计算与误差分析的文献均以简化或者设定喷嘴入口处空气密度来计算［1－4］，为了计算分析喷嘴流量测量装置的测量误差，本文根据喷嘴流量计算方法与误差分析原理，采用Matlab软件分项计算讨论了喷嘴直径的加工误差、喷嘴两端静压差、喷嘴前静压力、干球温度、相对湿度以及环境大气压力对喷嘴流量测量结果的影响.

1 喷嘴测量风量的计算

1.1 空气过滤器性能测试实验台简介

空气过滤器试验台是根据欧洲标准EN 779—2002及中国制冷空调工业协会标准《一般通风空气过滤器性能实验方法》（CRAA 432—2008）搭建的测试装置，除了可以测试各种一般通风空调空气过滤器（G1—F9级）的性能（效率、阻力及容尘量），通过增加部分附件还可对风机－过滤单元（FFU）以及其他空调通风部件（如风口、阀门、变风量VAV（variable air volume）末端装置等）进行性能试验研究［5－6］.图1为空气过滤器性能测试实验台示意图，其中流量测试装置采用1个直径为225mm与4个直径为80mm的标准长径低比值喷嘴，通过改变风机频率和喷嘴开启数量来达到受试过滤器的需求风量.

图1 空气过滤器性能测试实验台示意图Fig.1 Test rig for particulate air filter

1.2 空气流量测量计算

根据美国采暖、制冷与空调工程师学会（American Society of Heating，Refrigerating and Air－Conditioning Engineers）的 ASHRAE 42.1标准，通过单个喷嘴的空气流量按下式计算［7］：

式中：Qx为单个喷嘴的流体流量，m3·h－1；C为喷嘴流量系数；Ax为喷嘴喉部面积，m2；Y为膨胀因子；ΔP为喷嘴前后两端的静压差，Pa；ρx为喷嘴喉部的空气密度，kg·m－3.

膨胀因子Y可按下式计算［7］：

式中：β为喷嘴喉部直径dx与风量测量静压室直径D的比值，即β＝dx／D；α为喷嘴喉部断面空气压力与喷嘴入口断面空气压力比值.

α按下式计算：

式中：R为通用气体常数，287.1J·kg－1·K－1；tx为空气干球温度，℃.

对于L／dx＝0.6型标准空气流量喷嘴（L为喷嘴喉部长度），流量系数C可由下式确定［7－9］：

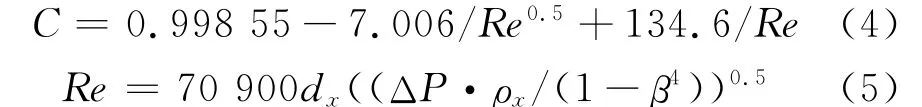
式中：Re为喷嘴喉部的雷诺数；喷嘴喉部的空气密度ρx计算式如下［10］：

式中：B为实验室环境大气压力，Pa；P为喷嘴入口处静压力，Pa；Pq为喷嘴入口处空气水蒸气分压力，Pa；ts为喷嘴入口处空气湿球温度，℃；RH为空气相对湿度，%.

严格的空气湿球温度ts计算较为复杂，需采用迭代才可计算出比较精确的值［11］，为方便喷嘴误差计算，本文的湿球温度采用如下回归式来计算：

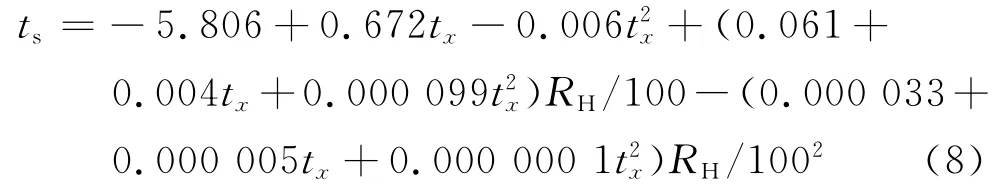
由此得到单个喷嘴流量Qx并对其进行修正，得到通过空气过滤器的流量Q′为

式中，ρ0为实验室的环境空气密度，风量测量静压室直径D为1m，整理得

多个喷嘴同时使用时，同一被测风量下的各个喷嘴出口动压值分布非常均匀［4］，因此通过流量测量装置的流体流量等于各个喷嘴所测流量之和

2 喷嘴流量计测量误差分析

根据误差合成定律，对于间接测量标准误差的传递公式［12］可得到如下喷嘴流量测试误差的计算公式：

式中：σQ′为喷嘴流量标准差，m3·h－1；σdx为喷嘴喉部直径标准差，m；σP为喷嘴入口处空气静压力标准差，Pa；σt为空气干球温度标准差，℃；σRH为空气相对湿度标准差，%；σΔP为喷嘴压差标准差，Pa；σB为空气大气压力标准差，Pa.

对于喷嘴直径的误差，根据贝塞尔公式

式中：dxi为喷嘴直径测量值，m；dx为喷嘴直径真值，m；n为测量次数.

对于单次测量的压力差ΔP，误差可由下式确定［1，12］：

式中：a为仪器精度；ΔPk为仪器量程；ΔP为压力差的读值.

喷嘴流量测量过程中喷嘴前静压力、喷嘴空气干球温度、相对湿度以及实验室环境大气压力都可归属为动态变化的单次测量，因此以上测量因子的标准差与喷嘴前后压力差ΔP的误差计算相同.

2.1 喷嘴流量测量装置误差计算

鉴于喷嘴流量计算公式较为复杂且影响因子较多，本文采用数值计算Matlab软件对计算式中影响因子分别求偏微分后获得相应的各因子对喷嘴流量的误差值.该实验台的喷嘴设计风量测量范围为155～7 000m3·h－1，不同喷嘴直径对应的标准差与不确定度值可见表1和表2，由此可得到各个喷嘴的σd／d值，从表中看出各个喷嘴的误差值满足喷嘴的加工精度范围值0.05%～0.20%［1］；喷嘴流量影响因子喷嘴前后压力差、喷嘴前静压力、空气干球温度、相对湿度以及实验室环境大气压力测量仪器的量程、测量范围与精度见表3，由此可计算得到相应的影响因子最大误差（σx／X）max值.

图2为喷嘴流量测量装置不同喷嘴组合下的流量测量误差，整个喷嘴测量装置的测量误差不超过0.018 2，测量误差较小.对于图中阴影部分的相同测试风量段，喷嘴的开启组合方式不同对应产生的测量误差也不尽相同，当开启1个80mm喷嘴与开启2个80mm喷嘴测量相同风量时，开启1个喷嘴产生的测量误差明显小于开启2个喷嘴产生的误差；同样在2 147～2 652m3·h－1的测试风量范围内，开启4个80mm喷嘴产生的流量测量误差小于同风量下开启225mm喷嘴时产生的测量误差，因此建议在选定喷嘴组合方式测试风量时应尽量使开启喷嘴达到其测量范围的极大值（即喷嘴流量在一定范围内大些），只有当喷嘴个数不能满足风量测量要求时再开启多个喷嘴，这样可以减少因喷嘴组合方式不同而产生的流量测量误差.

表1 喷嘴直径测量Tab.1 Results of the measurement for the nozzles’diameters

表2 喷嘴标准差及不确定度Tab.2 Standard error and uncertainty of the nozzles

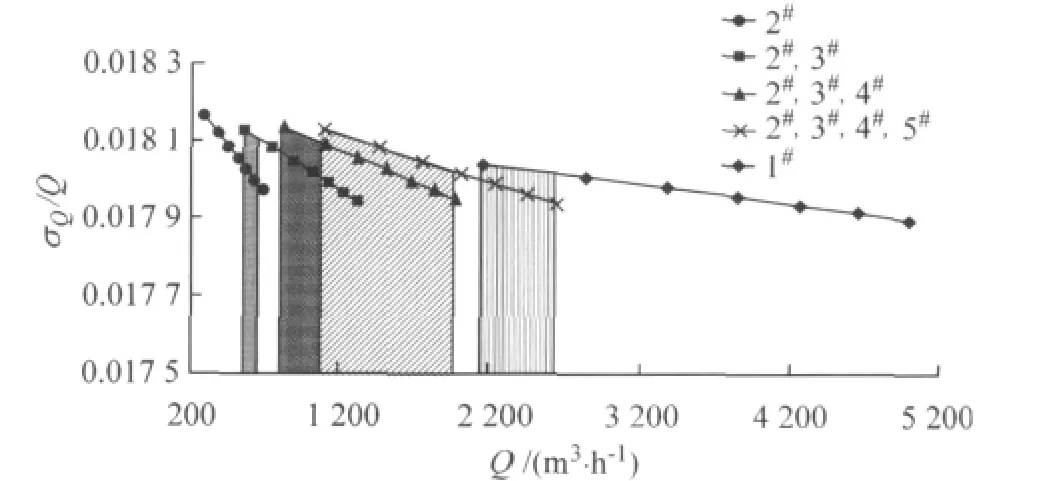
图2 不同测量风量下的流量误差Fig.2 Uncertainty for different air flow rates

对于同样风量下单个喷嘴的不同直径对喷嘴流量测量误差的影响可见图3，假定喷嘴直径σd／d加工精度均为0.05%，从图上可以看出：在相同的直径加工精度时，同样风量下喷嘴直径越小产生的测量误差越小，喷嘴直径产生的最大喷嘴流量测量误差不超过1.81%.由此可知，对于采用单个喷嘴测量相同的风量，直径较小的喷嘴可减小测量误差，在设计选择喷嘴流量计的喷嘴直径时可根据被测风量的范围选择合适大小的喷嘴或者喷嘴组.

表3 喷嘴流量影响因子的误差计算Tab.3 Error calculation of the factors on air flow rate measured by multiple nozzles

图3 不同喷嘴直径下的流量误差Fig.3 Uncertianty for different diameters of the nozzle

2.2 测量仪器精度对喷嘴流量的影响

根据喷嘴流量的计算公式与间接测量误差传递原理，空气过滤器实验台喷嘴流量测量的影响因子为喷嘴喉部直径、喷嘴前后压力差、喷嘴前静压力、喷嘴空气干球温度、相对湿度以及环境大气压力.图4为直径加工精度对喷嘴直径80mm的喷嘴流量误差的影响，一般标准喷嘴的直径加工精度范围为σd／d＝0.05%～0.20%［1］，可以发现喷嘴直径的加工精度对喷嘴标准流量的影响比较大，加工精度为0.20%与0.05%测量误差差值为0.042%，由此可见为提高喷嘴流量的测量精度，应选用加工精度较高的喷嘴.图5为喷嘴前后压力差仪器精度对喷嘴流量误差的影响，从图可见喷嘴压力差对喷嘴流量标准差的影响非常显著，当选用精度为2.5%的压力差计时，喷嘴误差最大可达到0.03，远远大于压力差仪器精度为0.5%时的喷嘴误差值0.006 1.喷嘴前后压力差应根据需求尽可能选用精度比较高的压力传感器，建议仪器精度至少不低于1.5%.

图4 直径加工精度对σQ／Q的影响Fig.4 The effect of the manufacturing precision of the nozzles’diameter onσQ／Q

图5 压力差计精度对σQ／Q的影响Fig.5 The effect of accuracy of the sensor for pressure difference onσQ／Q

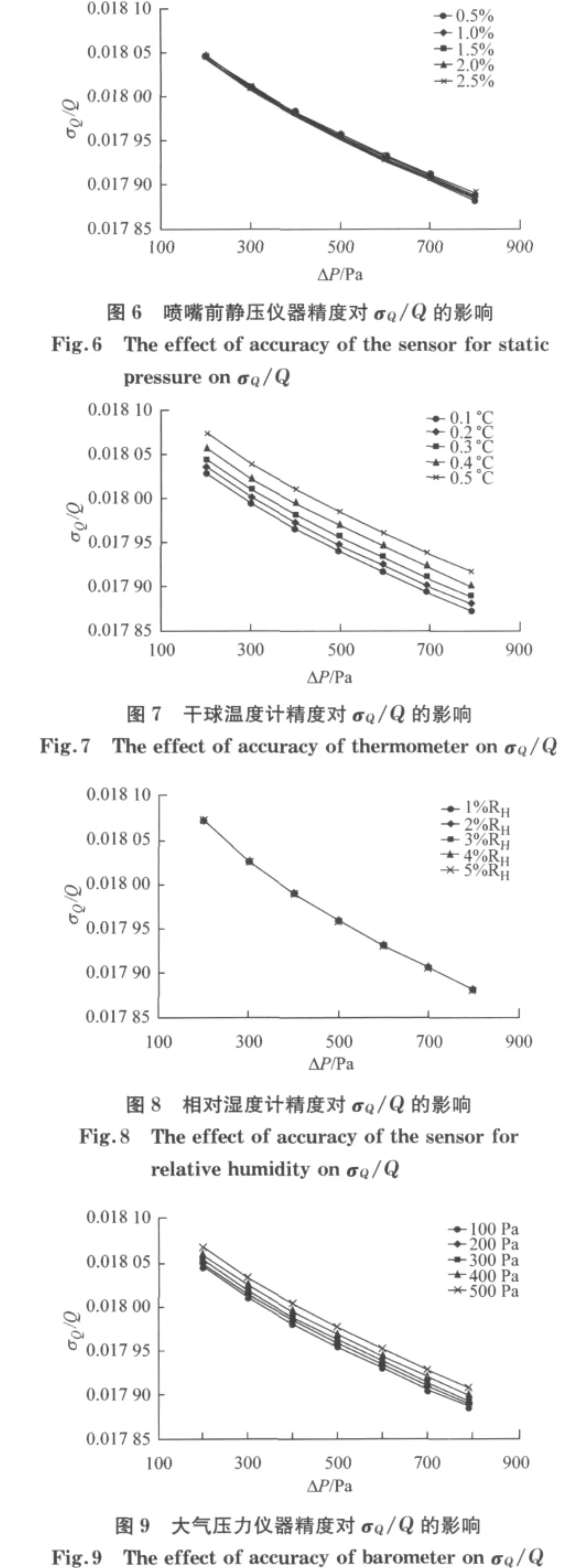
图6 —9分别为喷嘴直径D＝80mm的喷嘴前静压力、喷嘴干球温度、相对湿度以及环境大气压力对喷嘴流量误差的影响.喷嘴空气密度ρx的影响因子也为上述4个因子，因此可从4个因子对喷嘴误差的影响来判断喷嘴空气密度简化计算的合理性.图6表明喷嘴前静压力计不同的精度对喷嘴误差影响几乎可以忽略，当测量风量比较小时，不同精度的喷嘴误差基本保持不变，因此可选用一般精度的传感器测量喷嘴前静压.从图7中可以发现不同的干球温度的测量精度对喷嘴测量误差影响相对较小，精度为±0.5℃与±0.1℃的干球温度计对喷嘴流量测量产生的误差相差不超过0.005%，实验装置对于干球温度计精度选取时宜选用精度稍高的仪器.同样从图8中可以看出相对湿度仪器精度对于喷嘴误差几乎没有影响，这是由于相对湿度对喷嘴喉部的空气密度影响较小，对应的相对湿度仪器精度对喷嘴测量误差也比较小而基本可以忽略，故对于相对湿度计的仪器精度可不作高精度要求.图9为大气压力计精度对喷嘴误差的影响，相对而言大气压力计精度对喷嘴误差影响非常小，不同精度对喷嘴误差的差值不超过0.002%，大气压力计精度对喷嘴误差的影响在可接受的范围内.由此可见喷嘴空气密度的4个影响因子中干球温度计与大气压力计应选用精度稍高的仪器，静压力与相对湿度测量仪器的精度选用要求准确度较高的仪器即可，无须满足高精度的要求.

2.3 压力差计精度对不同喷嘴开启组合方式下流量测量误差的影响

通过以上的讨论发现压力差计的精度对整个喷嘴流量测量误差影响最大，而不同喷嘴开启组合方式也会对测量误差产生一定的影响，为此讨论更高精度的压差传感器对喷嘴测量误差的影响.图10为压差传感器为0.5%精度时不同喷嘴组合方式下的流量测量误差，压差传感器量程仍为0～1 000Pa，由此 （σΔP／ΔP）max＝0.011 9.从图中可以发现当压力传感器的精度提高2级之后，同样风量下不同喷嘴的开启组合方式对流量测量误差的影响明显减小，基本上可以不考虑不同喷嘴组合对喷嘴流量测量误差产生的影响，同时喷嘴流量计的测量误差降低到0.63%以下，比原来的1.82%有所提高，更好地满足过滤器性能实验对喷嘴流量测量装置的要求.本试验台实际上已将测量喷嘴两侧压差由原先采用的精度为1.5%的传感器更换为精度更高（0.5%）的压力传感器.

图10 不同喷嘴组合下的喷嘴流量测量误差Fig.10 The uncertainty of the air flow rate measurement for different nozzles combination

3 结论

（1）测量喷嘴前后两端压力差的仪器精度对喷嘴流量测量装置误差的影响最大，建议尽可能选用高精度的压力差计，仪器精度不低于1.5%；本空气过滤器性能试验台将压力传感器更换为0.5%精度后的喷嘴测量流量误差最大不超过0.63%.

（2）干球温度计与大气压力计对喷嘴流量测量产生的误差较小，可采用一般精度的仪器测量干球温度与环境大气压力.

（3）相对湿度计与静压力计的精度对喷嘴流量误差几乎没有影响，因此在保证仪器测量的准确度时无须满足高精度的要求.

（4）喷嘴直径加工精度对流量测量误差相对影响较大，需对出厂的加工精度进行验证.

（5）当测量喷嘴压差的压力传感器精度不高于1.5%时，相同风量下不同喷嘴组合方式不同对应产生的流量测量误差也不同，宜根据风量测试范围选用合适喷嘴组合以减少测量误差；测量时宜尽量使开启喷嘴接近其测量范围的极大值后再增加喷嘴开启个数.而采用0.5%精度的压差传感器，则可不考虑喷嘴组合方式的影响.

［1］王维新，陆亚俊.测量空气流量用标准喷嘴的误差分析［J］.沈阳建筑工程学院学报，1989，5（1）：23.WANG Weixin，LU Yajun.Error analysis of standard spray nozzle for determining air flow ［J］.Journal of Shenyang Architectural and Civil Engineering University，1989，5（1）：23.

［2］杨晚生，张艳梅，张吉光，等.空调通风试验台喷嘴流量测量装置误差分析［J］.流体机械，2004，32（1）：31.YANG Wansheng，ZHANG Yanmei，ZHANG Jiguang，et al.Error analysis on standard spray nozzle for measuring air flow of ventilation experimental instrument［J］.Fluid Machinery，2004，32（1）：31.

［3］刘贵琦，沈晋明.多功能通风部件试验台模块化控制分析［J］.洁净与空调技术，2007（4）：4.LIU Guiqi，SHEN Jinming.Analyses of blocking control on the multi－functional experimental instrument for ventilating parts［J］.Contamination Control ＆ Air－conditioning Technology，2007（4）：4.

［4］王天富.流量喷嘴及其在实验室风量测量中的应用［J］.西北建筑工程学院学报，1993（1）：62.WANG Tianfu.Air flow rate measuring nozzle and its application of air flow measurement in the laboratory ［J］.Journal of Northwestern Institute of Architectural Engineering，1993（1）：62.

［5］林忠平，肖小野，潘冬梅，等.风机过滤单元（FFU）的性能试验研究［J］.建筑科学，2008，28（8）：51.LIN Zhongping， XIAO Xiaoye， PAN Dongmei，et al.Experimental study on the performance of fan filter unit［J］.Building Science，2008，28（8）：51.

［6］林忠平，肖小野.风机－过滤器单元结构组件对其性能影响的初步探讨［J］.暖通空调，2010，40（8）：144.LIN Zhongping，XIAO Xiaoye.Preliminary study on fan－filter unit performances relating to the constituent components［J］.Heating Ventilating ＆Air Conditioning，2010，40（8）：144.

［7］American Society of Heating， Refrigerating and Airconditioning Engineers.ANSI／ASHRAE Standard 41.2—1987 RA92.Standard Methods for Laboratory Airflow Measurement［S］.Atlanta：ASHRAE，1987.

［8］Bohanon H R.Fan test chamber－nozzle coefficients ［J］.ASHRAE Transactions，1975，81：104.

［9］American Society of Heating， Refrigerating and Airconditioning Engineers.ANSI／ASHRAE Standard 51—2007.Laboratory methods of testing fans for certified aerodynamic performance rating［S］.Atlanta：ASHRAE，2007.

［10］赵荣义，范存养，薛殿华，等.空气调节［M］.3版.北京：中国建筑工业出版社，1994.ZHAO Rongyi，FAN Cunyang，XUE Dianhua，et al.Air conditioning［M］.3rd ed.Beijing：China Architecture and Building Press，1994.

［11］荣剑文.湿球温度的计算及应用［J］.制冷技术，2008（4）：38.RONG Jianwen.Calculation and application of wet bulb temperature［J］.Refrigeration Technology，2008（4）：38.

［12］徐大中.热工与制冷测试技术［M］.上海：上海交通大学出版社，1985.XU Dazhong.Thermal and refrigeration testing technology［M］.Shanghai：Shanghai Jiaotong University Press，1985.