基于改进粒子群优化算法的灰色神经网络模型

马军杰，尤建新，陈 震

（1.同济大学 法学院，上海200092；2.同济大学 经济与管理学院，上海200092）

灰色系统理论，是由我国学者邓聚龙教授于1982年首创的一种系统科学理论.在灰色系统中建立的模型称为灰色模型，即GM模型，它能对不确定系统行为特征值的发展变化进行预测［1］.灰色建模要求的样本点少，不必有较好的分布规律，神经网络具有并行计算、分布式信息存储、强容错力、自适应学习功能等优点.将灰色预测建模和神经网络技术融合起来，建立灰色神经网络模型（grey neural networks model，GNNM）［2］，可以充分利用两者在信息表现上存在的相似性及模型特点上存在的互补性，并能弥补单纯使用灰色模型或单纯使用神经网络解决问题的不足.

粒子群优化算法（particle swarm optimization，PSO）则是计算智能领域除蚁群算法、遗传算法之外的一种群体智能优化算法，该算法最早由Kennedy和Eberhart在1995年提出［3－4］.它具有搜索速度快、效率高的优点，早已广泛用于各类连续问题和离散问题的参数优化.然而粒子群算法同时存在搜索精度不高，容易陷入局部最优解的缺点.因此，本文借鉴遗传算法中的变异思想，在粒子群算法中引入变异操作，拓展种群搜索空间，使粒子跳出先前搜索的最优区域，在更大的空间中开展搜索，保持了粒子种群的多样性，提出了改进的粒子群算法.同时，根据灰色神经网络的参数随机选择类似于粒子群算法中的粒子初始空间位置，由计算误差不断调整网络参数的过程类似粒子群算法寻优过程，采用改进粒子群算法代替梯度修正法，修正网络参数，使网络输出不断逼近期望输出，建立了基于改进粒子群算法的灰色神经网络（改进PSO－GNNM），并进行了应用.

1 灰色神经网络［5］

设不确定系统的特征值的原始数列为（t＝0，1，2，…，N－1），经过一次累加生成后得到新的数列呈指数增长规律，因而可以用一个连续函数或者微分方程进行数据拟合和预测.记为y（t），N个参数的灰色神经网络模型的微分方程表达式为

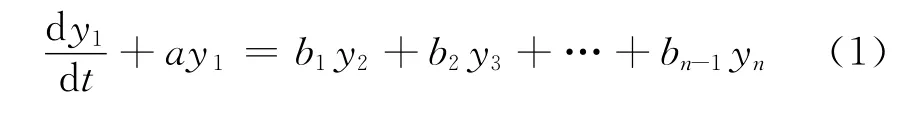
式中：y1为输出变量；yi（i＝2，…，n）为输入变量；a，bi为方程参数.式（1）解得表达式为

图1 灰色神经网络模型结构示意图Fig.1 Structure of grey neural networks model

图中输入变量权重为ω11＝a，输入层与隐含层权重为输出层与隐含层权重为ω3j＝1＋e－at，j＝1，…，n.

网络输出公式：

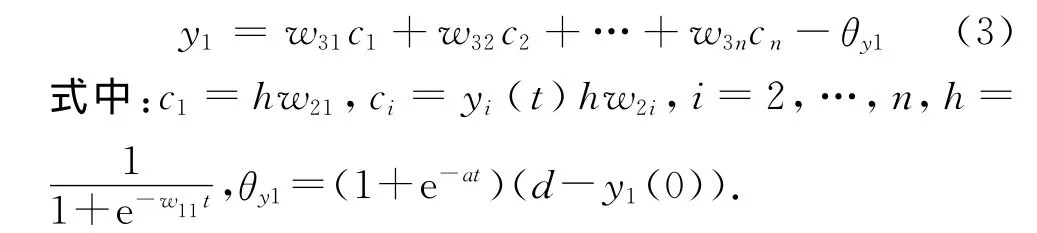
2 粒子群算法原理［6－7］

假设在一个D维的搜索空间中，由n个粒子组成的种群X＝（X1，X2，…，Xn），其中第i个粒子表示为一个D维向量Xi＝（xi1，xi2，…，xid）T，代表第i个粒子在D维搜索空间中位置，同时代表问题一个潜在解.将Xi代入目标函数计算其适应度值，根据适应度值大小衡量Xi是否为问题最优解.第i个粒子的速度为Vi＝（Vi1，Vi2，…，Vid）T，其个体极值为Pi＝（Pi1，Pi2，…，Pid）T，种群的全局极值为Pgd＝（Pi1，Pi2，…，Pid）T.迭代中，粒子通过个体极值和全局极值更新自身的速度和位置，更新公式如下［7］：

式（4），（5）中：c1，c2是加速系数，为非负常数，合适的c1，c2既可加快收敛又不容易陷入局部最优；r1，r2为［0，1］之间的随机数；ω为惯性因子；粒子在解空间内不断跟踪个体极值与全局极值进行搜索，直到达到规定的最大迭代次数或者规定的误差标准.为防止粒子的盲目搜索，将粒子位置和速度限制在［－Xmax，Xmax］，［－Vmax，Vmax］.

3 改进PSO－GNNM算法

粒子群算法容易早熟收敛、搜索精度较低、后期迭代效率不高等缺点［8］.为克服这些缺点，借鉴遗传算法中的变异思想，在算法中引入变异操作，在粒子每次更新之后，以一定概率重新初始化粒子.假设选择第i个粒子的第j个基因xij进行变异，变异操作方法如下：

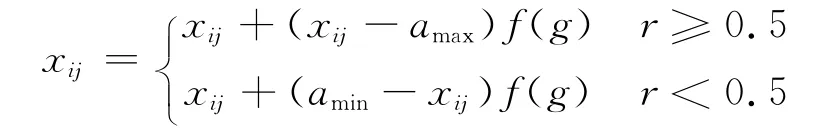
其中，f（g）＝rand（1－g／Gmax），g，Gmax分别是当前和最大迭代次数；amax，amin分别是xij的上界和下界；r是［0，1］间随机数.

同时为更好地平衡算法的全局搜索和局部搜索的能力，采用线性递减惯性权值，公式为

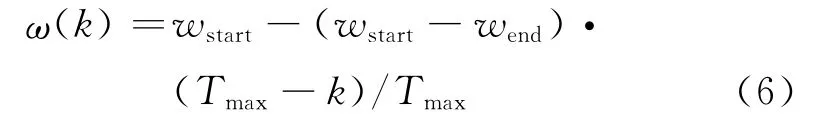
式中：wstart为初始惯性权值；wend为最终迭代惯性权值；Tmax为迭代次数；k为当前迭代次数.采用改进粒子群算法，代替梯度修正法，修正灰色神经网络参数.算法实现步骤如下：

（1）对初始数据归一化，再对数据进行累加.

（2）网络初始化.对粒子群算法的加速系数c1，c2，最大循环次数maxgen，种群规模sizepop，最大位置Xmax，最大速度Vmax，遗传变异概率进行初始设定.

（3）根据输入输出样本对确定灰色神经网络结构.根据网络结构确定待优化的网络参数a，bi，网络参数个数即为种群长度.

（4）种群初始化.随机产生sizepop个初始种群Xi，由Xi计算其适应度值fit，i.适应度采用灰色神经网络输出的平均绝对误差.平均绝对误差函数为

式中：yik为测试集的预测值；tik为测试集的真实值；n为测试集的个数；m为输出接点个数.

根据计算的适应度值，找出最小的fit，min适应度值对应的个体Xmin.令ZXmin＝Xmin，Zfit，min＝fit，min，ZXmin为最终的最优个体，Zfit，min为最终的最优适应度值.

（5）启动循环，根据式（4），（5）更新粒子的位置Xi和速度Vi，再以一定的概率初始化种群Xi到更新的X′i.由更新的X′i计算其适应度值f′it，i.

（6）比较fit，i和f′it，i大小，如果fit，i＞f′it，i，则Xi＝X′i，以保留优秀的个体.

（7）经过步骤（4）、（5）的Xi为新一代的个体.寻找最小 的fit，min，及其 对应的Xmin.如果fit，min＜Zfit，min，则ZXmin＝Xmin，否则不操作.

（8）循环步骤（4）～（6），当循环迭代达到最大次数时结束循环，并输出计算结果Zfit，min，ZXmin.

（9）把ZXmin赋给灰色神经网络参数a，bi，进行下一步的计算和结果输出.

4 数据与模型应用

（1）基本资料：本文选用的为36个月的冰箱销量数据（表1），来自文献［9］（限于篇幅，并且由于本文以算法优化设计为目标，因而对数据本身的详细说明进行了省略）.该数据已经经过归一化处理.影响冰箱市场需求量还有很多因素，这里选择需求趋势、市场份额、价格波动、订单满足率和分销商联合预测等5个因素作为主要因素预测冰箱订单量.

（2）对原始数据进行一次累加.确定样本对，根据样本对确定的灰色神经网络结构为1－1－6－1，粒子群种群长度为6.选择前30个月的数据为训练数据训练网络，后6个月的数据为验证数据.

（3）网络初始化.粒子群种群规模为500，迭代500次，两个加速系数因此都取1.4，权值因子开始为0.9，随着迭代的进行减小到0.1，最大位置和最大速度均取1.初始惯性权值取0.9，最终惯性权重取0.1.变异概率取0.81，个体范围上下限都分别取1和0.001.

表1 36个月的冰箱销售数据Tab.1 36months’data of refrigerator sales

（4）用30个样本进行训练，得到的最优解赋给灰色神经网络进行计算.

（5）计算结果见图2，并和BP神经网络，灰色神经网络，没有改进的粒子群算法模型［9］进行比较，平均绝对误差比较结果见表2.

通过验证结果分析能够看出，相比反向传播（BP）神经网络，GNNM要更好，BP神经网络有过拟现象；相比未优化的模型，优化后的模型要好于未优化的模型；改进粒子群算法的好于未改进的.改进模型PSO－GNNM的预测结果优于GA－GNNM模型结果.改进PSO－GNNM模型的优越性、平均绝对误差好于其他模型，可为生产实践提供更为准确的理论依据.

图2 改进PSO－GNNM网络预测图Fig.2 Forecasting result of modified PSO－GNNM

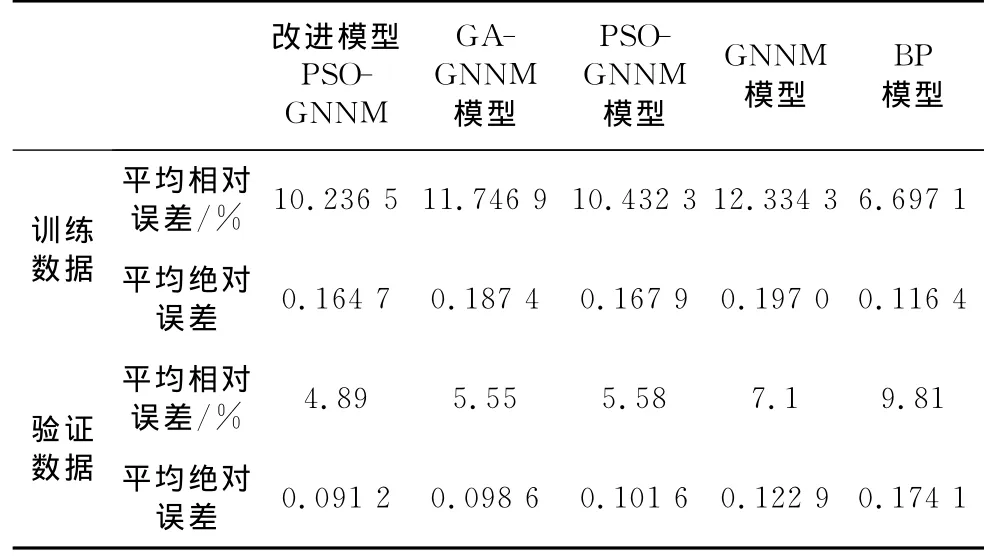
表2 改进PSO－GNNM模型运行结果与其他预测模型比较Tab.2 Running result comparison of modified PSOGNNM and other forecasting models

5 结论

（1）本文利用改进粒子群算法与灰色神经网各自的优点进行耦合，用改进的粒子群算法代替梯度下降法，调整网络的权值，用灰色神经网络输出的均方误差作为粒子适应度值，实现了灰色神经网络模型参数的优化，弥补了传统算法当中的部分缺陷.

（2）以冰箱短期订单量为实例进行模型仿真.实例表明，相比其他模型，改进PSO－GNNM模型计算的平均绝对误差更小，精度更高，更符合实际订单.在生产实际中，可以根据建立的模型，对市场进行预测，为生产管理服务，提高管理决策的科学性.

（3）本文所提出的改进粒子群优化算法的灰色神经网络模型为短期订单预测研究提供了科学，有效的新途径，为了解需求趋势、市场份额、价格波动、订单满足率和分销商联合预测和冰箱销量关系提供了一个总体认识.

［1］邓聚龙.灰色系统基本方法［M］.武汉：华中科技大学出版社，2005.38-42.DENG Julong.The primary methods of grey system theory［M］.Wuhan：Huazhong University of Science and Technology Press，2005.38-42.

［2］袁景凌，钟珞，李小燕.灰色神经网络的研究及发展［J］.武汉理工大学学报，2009（3）：91.YUAN Jingling，ZHONG Luo，LI Xiaoyan.The research and development of grey neural network［J］.Journal of Wuhan University of Technology，2009（3）：91.

［3］Kennedy J，Eberhart R C.Particle swarm optimization［C］／／Proceedings of IEEE International Conference on Neural Networks.Perth：IEEE Press，1995：1942-1948.

［4］Eberhart R C，Kennedy J.A new optimizer using particle swarm theory［C］／／Proceedings of the Sixth International Symposium on Micromachine and Human Science.Nagoya：IEEE Press，1995：39-43.

［5］刘仁涛，付强，冯艳，等.基于RAGA的灰色神经网络预测模型及其对三江平原地下水埋深的动态预测［J］.系统工程理论与实践，2008（5）：171.LIU Rentao，FU Qiang，FENG Yan，et al.Grey BP neural networks model based on RAGA and its application in groundwater dynamic prediction of the Sanjiang plain［J］.Systems Engineering—Theory ＆Practice，2008（5）：171.

［6］张国华，张展羽，邵光成，等.基于粒子群优化算法的灌溉渠道配水优化模型研究［J］.水利学报，2006，37（8）：1004.ZHANG Guohua，ZHANG Zhanyu，SHAO Guangcheng，et al.Optimization model for discharge distribution of irrigation channels based on particle swarm optimizer［J］.Journal of Hydraulic Engineering，2006，37（8）：1004.

［7］王波，王灿林，梁国强.基于粒子群寻优的D－S算法［J］.传感器与微系统，2007，26（1）：84.WANG Bo，WANG Canlin，LIANG Guoqiang，D－S algorithm based on partical swarm optimizer［J］.Transducer and Miero Systerm Technologies，2007，26（1）：84.

［8］张志英，杨克开，于瑾维，等.改进粒子群算法的动态空间调度方法［J］，哈尔滨工程大学学报，2009，30（12）：1344.ZHANG Zhiying，YANG Kekai，YU Jinwei，et al.Dynamic spatial scheduling approach based on improved particle swarm optimization algorithm ［J］.Journal of Harbin Engineering University，2009，30（12）：1344.

［9］史峰，王小川，郁磊，等.Matlab神经网络30个案例分析［M］.北京：北京航空航天大学出版社，2010.258-265.SHI Feng，WANG Xiaochuan，YU Lei.Matlab neural network analysis of 30 cases［M］.Beijing：Beijing University of Aeronautics ＆Astronautics Press，2010.258-265.