间断型三向TMD桥梁颤振控制

徐家云，赵 勇，王雄江，陈 吉

（1.武汉理工大学 道路桥梁与结构工程湖北省重点试验室，湖北 武汉430070；2.武汉理工大学 土木工程与建筑学院，湖北 武汉430070；3.湖北省建筑科学研究设计院，湖北 武汉430071）

随着大跨轻柔桥梁结构的快速发展，桥梁风致振动的问题日益突出.为提高桥梁结构的安全性和稳定性，国内外的学者采取了许多有效的控制措施来控制桥梁振动，这些措施包括在主梁上增设减小涡振振幅的抑流板，提高颤振临界风速的裙板、导流板，降低驰振响应的转向装置，改变气动力的主梁开槽方案等气动措施［1－2］，还包括调谐质量阻尼器（tuned mass damper ，TMD）［3］、调谐液体阻尼器（tuned liquid damper，TLD）［4］、粘滞阻尼器［5］、磁流变（MR）阻尼器［6］等机械措施，其中TMD应用较为广泛.单个TMD减小结构的第一阶模态振动有明显的效果，但对高阶模态振动的效果不很明显［7］；沿全桥布置的多个TMD即多重调谐质量阻尼器（multiple tuned mass dampers，MTMD）理论上能取得较好的效果，但是这种MTMD的布置、维修和经济问题都是其广泛推广的障碍［8］，MTMD无控制扭转作用.

鉴于此，提出能同时控制桥梁横向、竖向和扭转三个方向振动的间断型三向TMD，间断型三向TMD就是分区布置的多个三向TMD或分区连续布置的三向TMD，前者与MTMD类似，后者为分区连续型三向TMD，并且提出与其相应的理论和计算方法，同时结合风洞试验和Ansys软件模拟来验证间断型三向TMD的控制效果.

1 间断型TMD控制桥梁风致振动计算模型

间断型三向TMD在桥梁结构断面中的布置如图1所示，在保证桥梁其他功能设施不受影响的情况下（如桥梁检修通道），将沿桥方向有针对性地间断布置在桥梁箱梁内，如布置在桥梁跨中或跨中一段范围内.规定桥梁横截面竖向振动向上为正（y），横向振动向右为正（z），轴沿桥长方向，指向纸内（x），扭转振动以顺时针为正.

图1 桥梁与TMD模型Fig.1 Model of the bridge-TMD system

在建立桥梁主结构体系风致振动的简化模型时，据文献［9］，假定主梁是平直等截面梁，质量均匀分布，而且每个断面都有相同的气动性能，即具有相同的颤振导数曲线［10］.另外，还假定风场特性沿桥长方向保持不变，来流风的方向总与桥梁轴线垂直，一般情况下这是最不利情况.根据桥梁模型得出模型的振动方程如式（1）.

此种TMD安装方式能同时控制桥梁结构三个方向的振动，两排竖向弹簧控制桥梁结构竖向振动，同时能控制风作用下的扭转振动.两横向弹簧控制桥梁横向振动.

式中：分别为桥梁单位长度的质量和截面转动惯量；Iz，Iy分别为桥梁断面x和y方向的惯性矩；E1Iω，GJp分别为桥梁断面约束扭转刚度和自由扭转刚度；m，I分别为单位长度内质量块的质量和截面转动惯量分别为桥梁各相应方向振动阻尼；k，c分别为质量块弹簧刚度和阻尼；d为竖向弹簧到纵轴y的距离；（x，t）（x，t）（x，t）分别为桥梁各相应方向的振 动速度；（x，t），（x，t），（x，t）分别为桥梁各相应方向的振动加程度；y（x，t），z（x，t），θ（x，t）分别为桥梁各相应 方 向振动位移；yi，zi，θi分别为i位置处质量块各方向的振动位移；δ为狄拉克函数；沿全桥共有n个TMD；L，D，M分别是气动升力、气动阻力和气动扭矩，表达式如式（2）.

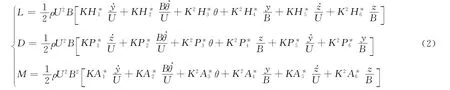
式中：ρ为空气密度；U为风速；B为桥宽；K＝ωB／U，ω为桥梁振动频率；、、（i＝1，2，…，6）为颤振导数.

在计算桥梁结构颤振临界风速时，桥梁结构的不稳定状态（发散振动）是一种大变形运动，属于非线性振动的范畴，但是仍可以应用线性振动理论来计算颤振临界风速.

在结构动力学理论中，线性弹性体系的小幅振动可以分解成一系列基本振型的组合，因此在计算桥梁结构颤振临界风速时，结构振动三个方向的位移相应可以写成式（3）的形式.

取前n个模态，采用振型分解法可设：

式中：qyr，qzr，qθr分别为第r振型下竖向、横向及沿桥纵轴转动方向的广义坐标；φr（x）为第r振型下桥梁主梁单元的位移函数.

经过最优控制理论整理可得：

式中：Qy，Qz，Qθ分别为广义坐标qyr，qzr，qθr组成的向量；Cj、Dj均是m，k，c和风速U的函数矩阵.只有当方程左端的矩阵为非奇异时，方程（4）才有解.

式（4）实际上就是个二次特征值问题，求解该方程将得到2n个特征值和相应的特征向量.当求解的λ的实部为零时，就标志着结构颤振失稳的发生，这样颤振临界风速就是当一对特征值的实部等于零的最低风速.

令λ实部为零，因为λ实部是m、k、c和风速U的函数，那么风速U是m、k、c的函数，为求最大的临界风速（若m已知），则分别对k、c求导，求出U的极值及相应的k、c，如此反复计算，即可得出最优的k、c和临界风速.

2 实桥模型风洞试验及Ansys软件模拟

本文以国内某长江公路大桥为背景，大桥主跨为926m的钢-混凝土混合梁斜拉桥，主梁断面采用分离双箱断面（亦称P－K断面），边跨主梁为混凝土，主跨主梁为钢.这种分离双箱主梁断面应用在千米级斜拉桥上还是第一次，其抗风性能如何是大桥设计最为关注的问题之一.为此，本文研究选取该桥为背景工程进行研究.

桥梁结构安装间断型三向TMD后，桥梁断面图如图2所示，结构的动力计算模型如式（5），式（5）的计算方法与式（1）的计算方法类似，这里不再赘述.与式（1）最大的不同是三向调谐质量阻尼器放在P－K断面两箱内能充分发挥其抗扭作用，式（5）第3个式子从理论上阐述了此问题.

图2 实桥安装TMD后断面图（左右对称）（单位：cm）Fig.2 Bridge section after the installation of TMD（symmetrical）（unit：cm）

该桥的风洞试验在湖南大学风洞试验室进行，采用节段模型，测试其三分力系数、颤振导数和无控制状态下的颤振临界风速等，其中采用强迫振动法来识别节段模型的颤振导数.

利用风洞试验得到的颤振导数，对全桥做Ansys软件模拟，Ansys模拟用单梁模型，主梁用Beam188和Beam4单元，刚性横梁用Beam4单元，桥塔用Beam4单元，斜拉索用Link10单元，调谐质量阻尼器控制器中质量块采用Mass21单元，弹簧和阻尼器采用Combin14单元.

桥面受到的气动自激力采用Ansys中的自定义单元Matrix27来模拟.Matrix27是Ansys中功能很强大的一种单元，该单元具有两个节点，每个节点都有6个自由度，它没有固定不变的几何形状，可以通过实常数的方式输入对称或不对称的质量、刚度或阻尼矩阵，每个桥梁节点上都有两个Matrix27单元（一个气动刚度单元和一个气动阻尼单元），每个单元都有一个节点为桥梁节点，另外一个节点固定不动，详见图3.图中：e为桥梁截面单元，e1和e3、e2和e4分别是桥梁截面两端气动刚度单元和气动阻尼单元，均为Ansys软件中的Matrix27单元，k、l两节点固定不动.

图3 Matrix 27单元布置详图Fig.3 The layout of the matrix 27elements

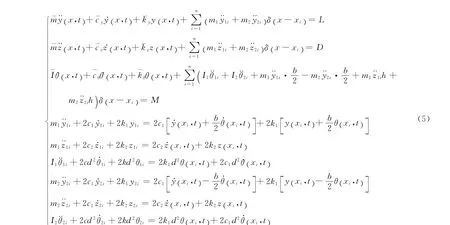
根据气动力学原理可导出这4个Matrix27单元的气动刚度或气动阻尼矩阵并组成单元气动力矩阵后就可得到总体气动力矩阵：

式中：Fae、Kae、Cae分别代表总体气动力向量、气动刚度矩阵、气动阻尼矩阵.

将式（6）代入到整个桥梁与TMD系统中得：

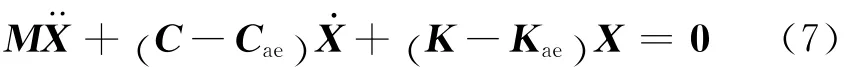
式中：M、C、K分别为桥梁的质量矩阵、阻尼矩阵和刚度矩阵；式（7）描述了风、桥梁结构和TMD系统的运动方程，其中风速和振动频率为系统参数，整个系统中共有n对共轭特征值λj＝σj±iωj，如果所有特征值的实部σ小于0，则系统是稳定的；如果至少有一对特征值的实部大于0，则结构颤振失稳发生.颤振临界风速就是当一对特征值的实部等于0的最低风速.无控制器的颤振临界风速vcr为109m·s－1（图4）.

桥梁模型加上TMD后，TMD布置在桥梁中跨一段距离内，每个三向TMD的参数都一致，竖向弹簧刚度为k1，横向弹簧刚度为k2（k1、k2均为布置范围内单位长度的弹簧刚度），据文献［11］，TMD系统两个方向的阻尼比都是0.07.

图4 无TMD时的颤振临界风速Fig.4 Flutter critical wind speed without TMD

针对不同的k1（k2＝80kN·m－1不变，总质量m＝500t不变，这为主跨总质量的3.0%左右），做了若干个工况的Ansys计算，在计算过程中着重考虑了桥梁和TMD组合结构的前二十阶模态.通过大量计算可知：k2的取值大小对颤振临界风速影响极小，故取k2＝80kN·m－1（此值为控制抖振所用）；当k1、k2一定时，特征值λj＝σj±iωj的实部随风速的变化而变化，最重要的几阶复特征值的实部随风速的变化而变化的情况如图5～图8所示（只包括四个重要复特征值），图5～图8中各工况的颤振临界风速vcr分别为125，137，123，137m·s－1.复特征值λj＝σj±iωj的实部和虚部分别对应着结构振动的阻尼和频率，当σj为趋于零时，说明桥梁振动开始发散，对应的风速即为颤振临界风速.

三向TMD在桥梁上布置分为两种情况：一种三向TMD布置在桥跨中央12m范围内，简称为“布置一”；另一种三向TMD布置在桥跨中央72m范围内，简称为“布置二”.两种布置中，颤振临界风速随k1的变化而变化的情况见表1～表2.计算时单个TMD质量取到300t，这还不到主跨质量的2%，此时颤振临界风速只有112m·s－1，仅提高2.7%，又

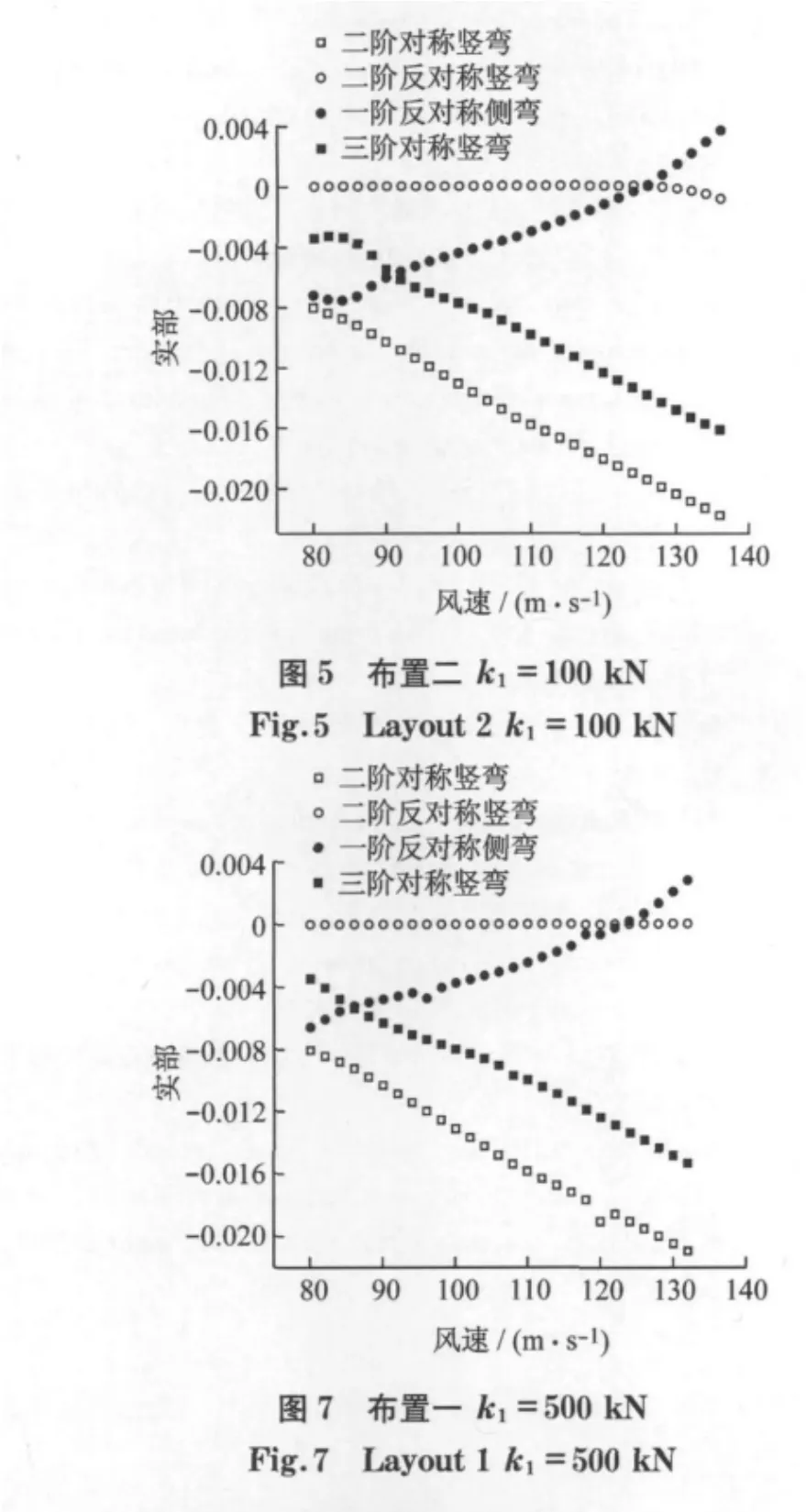
表1 布置一颤振临界风速变化情况Tab.1 Flutter critical wind speed in Layout 1

3 结论

本文为提高桥梁结构的颤振临界风速，采用间断三向TMD对其进行控制.通过风洞试验和Ansys软件模拟，主要对桥梁结构的颤振临界风速做了分因桥横截面及检修通道的限制，单个TMD的质量就不可能很大，故单个TMD对大跨桥梁控制效果不理想.析研究，得出以下结论：

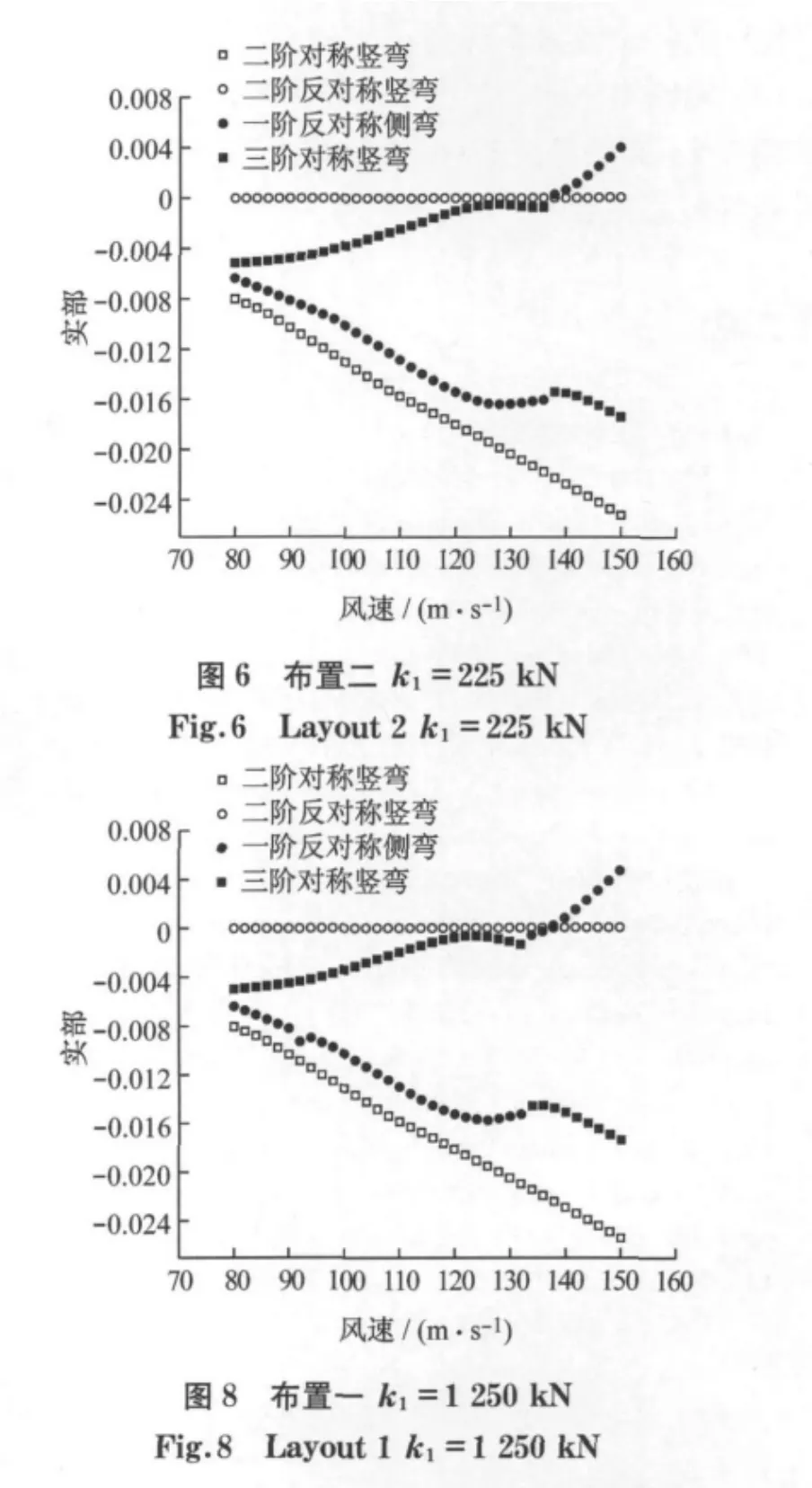
表2 布置二颤振临界风速变化情况Tab.2 Flutter critical wind speed in Layout 2

（1）本文提出了“间断型控制”概念，针对桥梁单个TMD或MTMD不足，对桥梁风致振动采用间断型TMD控制；

（2）根据桥梁振动控制要求，提出了风致振动三向控制器，使其既能控制桥梁横向、竖向振动，同时又能控制桥梁结构扭转振动；

（3）间断型三向TMD能有效提高桥梁结构的颤振临界风速，当三向TMD布置在桥梁跨中一段范围内，桥梁颤振临界风速能提高约13%～25%；单个TMD的控制效果不理想；

（4）间断型三向TMD布置较为灵活，能根据不同的需要，不同的经济条件，按照要求对桥梁结构进行针对性较强的控制.

［1］宋锦忠，林志兴，徐建英.桥梁抗风气动措施的研究及应用［J］.同济大学学报：自然科学版，2002，30（5）：618.SONG Jinzhong，LIN Zhixing，XU Jianying.Research and appliance of aerodynamic measures about wind－resistance of bridges［J］.Journal of Tongji University：Natural Science，2002，30（5）：618.

［2］林志兴，葛耀君，曹丰产，等.钢箱梁桥的抗风问题及其对策研究［J］.同济大学学报：自然科学版，2002，30（5）：614.LIN Zhixing，GE Yaojun，CAO Fengchan，et al.Wind resistant study and prevention research of steel box girders［J］.Journal of Tongji University：Natural Science，2002，30（5）：614.

［3］Chang C C，ASCE M，Gu M，et al.Tuned mass dampers for dual－mode buffeting control of bridges［J］.Journal of Bridge Engineering，2003，8（4）：237.

［4］Xue S D，Ko J M，Xu Y L.Wind－induced vibration control of bridges using liquid column damper ［J］.Earthquake Enginerring and Engineering Vibration，2002，1（2）：271.

［5］梁剑青，欧进萍.大跨斜拉桥桥面风致抖振的粘滞阻尼控制分析［J］.地震工程与工程振动，2006，26（1）：139.LIANG Jianqing，OU Jinping.Lateral buffeting control of long span cable stayed bridge deck by viscous dampers ［J］.Earthquake Engineering and Engineering Vibration，2006，26（1）：139.

［6］姜天华，霍凯成，瞿伟廉.天兴洲长江大桥风致抖振反应的控制［J］.武汉理工大学学报，2007，29（1）：121.JIANG Tianhua，HUO Kaicheng，QU Weilian.Control of wind induced lateral buffeting responses of tianxingzhou bridge［J］.Journal of Wuhan University of Technology，2007，29（1）：121.

［7］曾宪武，韩大建.多重双频率调谐质量阻尼器制振性能及对桥梁抖振的控制［J］.工程力学，2006，23（1）：74.ZENG Xianwu， HAN Dajian.Vibration suppression characteristics of multiple tuned mass dampers with dual frequencies and its application to buffeting control of bridges［J］.Engineering Mechanics，2006，23（1）：74.

［8］李春祥，余琼，王肇民.大跨桥梁结构扭转振动的MTMD控制研究［J］.特种结构，2002，19（4）：66.LI Chunxiang，YU Qiong，WANG Zhaomin.Torsional vibration control of large span bridges using multiple tuned mass dampers［J］.Special Structure，2002，19（4）：66.

［9］项海帆.现代桥梁抗风理论与实践［M］.北京：人民交通出版社，2005.XIANG Haifan.Theory and practice of the modern bridges［M］.Beijing：China Communications Press，2005.

［10］陈政清.桥梁风工程［M］.北京：人民交通出版社，2005.CHEN Zhengqing.Wind engineering of bridges［M］.Beijing：China Communications Press，2005.

［11］徐家云，刘科，常英，等.桥梁连续型控制颤振理论研究［J］.华中科技大学学报，2011，39（5）：55.XU Jiayun，LIU Ke，CHANG Ying，et al.Continuous controlling flutter theory of the bridges structures［J］.Journal of Huazhong University of Science and Technology，2011，39（5）：55.