流变模型在隧道监控数据处理中的应用
胡 翔
(中铁二局股份有限公司,贵州贵阳 550003)
用新奥法开挖隧道的一个重要特征就是在施工过程中对隧道围岩变形情况进行监控量测,以便根据围岩变形情况调整施工方案,指导施工。但是,由于施工干扰等因素的影响,现场直接量测得到的数据往往具有较大的离散性,需要用数学方法处理后才能在工程中应用,而回归分析就是其中最常用的数学处理方法。通过回归分析,可以建立围岩变形量与时间之间的函数关系式,这对于分析围岩变形趋势、预测最终变形量和决定二次衬砌时间等均具有非常重要的意义。
以往常用的回归函数有指数函数、对数函数、幂函数以及双曲线函数等[1-3],但是这些函数表达式由于模型参数较少(一般2个),预测精度往往较差。于是不少学者提出用多参数的回归方程对隧道围岩变形数据进行拟合,如 Weibull函数[4]、MMF函数[5]等,并且取得了非常好的效果。但是通过分析可以发现,用这些函数对隧道围岩变形情况进行回归分析,往往只是纯数学上的曲线拟合,各模型参数不具有物理意义。基于此,本文采用流变模型来对隧道围岩变形情况进行预测和分析。
1 预测模型的提出
开尔文模型[6]是岩石流变学中应用最为广泛的模型之一,由一个虎克体和一个牛顿体并联组成,如图1所示。

虎克体是一种理想的弹性体,其本构关系满足虎克定律,即:

式中:σ——应力;
ε——变形量;
E——弹性模量。
牛顿体是一种理想的粘性体,符合牛顿流动定义,即:

式中:η——粘滞系数;
由于两元件并联,则变形相等,应力叠加,即:

解微分方程,并根据初始条件,可得开尔文模型的变形量为[6]:

其中,t为时间,其余符号意义同前。
对于某一特定工程而言,如隧道开挖后未施作二次衬砌之前,隧道围岩应力σ近似认为是恒定值,则式(4)中σ/E,E/η均为常数,令a=σ/E,b=E/η,同时围岩变形量以u表示,则式(4)变为:

式(5)即为以开尔文模型表示的隧道围岩变形量预测函数或者叫回归方程。若能测得围岩应力,则可进一步计算出围岩体的弹性模量E和粘滞系数η。
若以式(5)对隧道围岩变形量进行预测,由于只有两个参数,则拟合精度可能会稍差。此时,可在开尔文模型的基础上再串联一个开尔文模型,形成广义开尔文模型,如图2所示。
根据叠加原理,可得广义开尔文模型的变形量表达式[6]为:

令 a1= σ/E1,b1=E1/η1,a2= σ/E2,b1=E2/η2,进行变量代换,同时围岩变形量以u表示,则有:
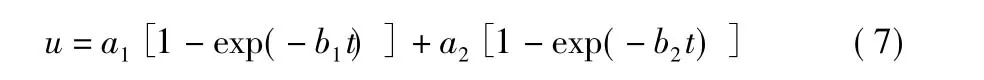
式(7)即为以广义开尔文模型表示的隧道围岩变形量预测函数。
2 模型的验证
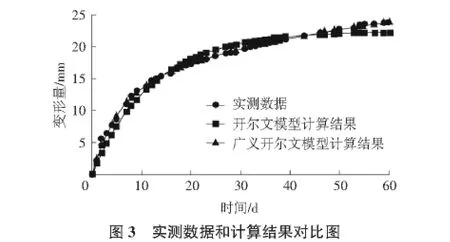
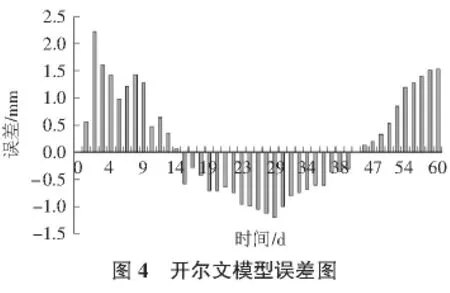
某隧道1断面自开挖起60 d的拱脚净空收敛实测数据如表1所示。分别以开尔文模型和广义开尔文模型即式(5)和式(7)对实测数据进行回归分析,表1同时给出了计算结果和拟合误差,图3~图5给出了计算结果和实测结果对比图和误差对比图。
由表1中实测数据和两种模型计算结果的对比分析可以看出:在开尔文模型计算结果中,误差绝对值在2 mm以上的有1个,占总数的2.22%;误差绝对值在1.5 mm~2 mm的有3个,占7%;误差绝对值在1 mm~1.5 mm的有11个,占24.44%;误差绝对值在0.5 mm~1 mm的有17个,占37.78%;误差绝对值在0 mm~0.5 mm的有13个,占28.89%。在广义开尔文模型计算结果中,误差绝对值在1 mm以上的有1个,占2.22%;误差绝对值在0.5 mm~1 mm的有1个,占 2.22%;误差绝对值在 0 mm ~0.5 mm的有43个,占95.56%。由此可以看到,开尔文模型计算结果与实测结果的误差较大,而广义开尔文模型计算结果与实测数据吻合良好,误差非常小。
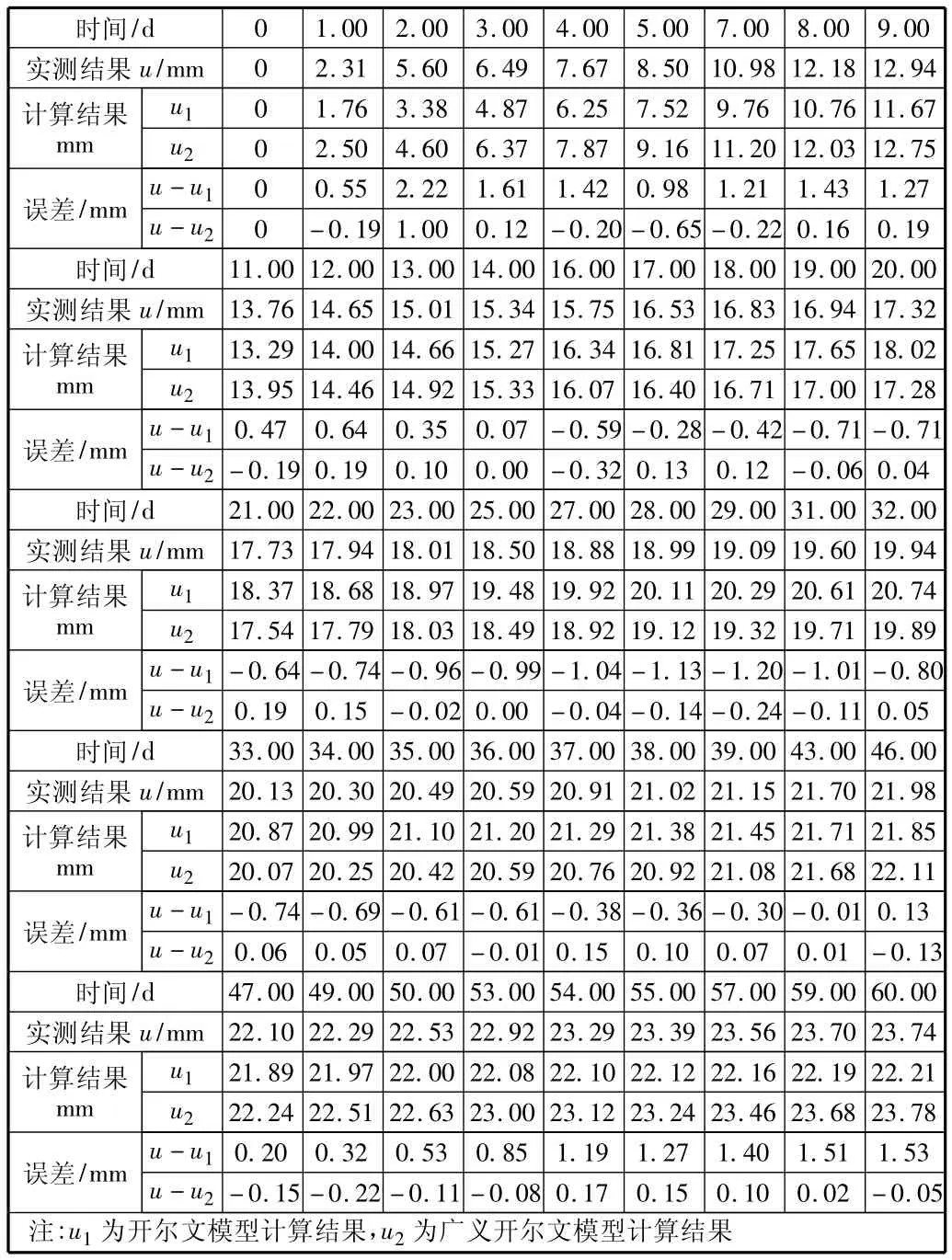
表1 实测变形量与计算结果对比表
同时从图3~图5也可以非常直观的看出,广义开尔文模型在数据处理分析中具有较大的优势,非常适合作为回归函数对隧道围岩变形数据进行回归分析和预测。

3 结语
1)针对以往常用的隧道围岩变形预测回归函数模型参数物理意义不明确的缺点,本文以岩石流变分析中广泛应用的开尔文模型和广义开尔文模型作为回归函数对隧道围岩变形量与时间的关系进行了回归分析和预测,取得了良好的效果。2)从本文实例中开尔文模型和广义开尔文模型的拟合效果来看,开尔文模型计算结果与实测结果的误差较大,而广义开尔文模型计算结果与实测数据吻合良好,误差非常小。3)广义开尔文模型在数据处理分析中具有较大优势,能够很好的反映隧道围岩变形量随时间的变化规律,可以为指导施工提供充分的理论依据。因此,该模型非常适合作为回归函数对隧道围岩变形数据进行回归分析和预测。
[1] 李晓红.隧道新奥法及其量测技术[M].北京:科学出版社,2001.
[2] 李世辉.隧道围岩稳定系统分析[M].北京:中国铁道出版社,1991.
[3] 王军保,张 乔,包 太.一元非线性回归分析在隧道监控中的应用[J].贵州工业大学学报,2007,36(6):63-66.
[4] 游 强,毕忠伟.生长曲线模型在隧道监控数据处理中的应用[J].宁夏大学学报(自然科学版),2011,32(2):127-129.
[5] 包 太,税 月.MMF生长模型在隧道监测数据分析中的应用研究[J].贵州大学学报(自然科学版),2009,26(4):131-133.
[6] 蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2002.
——以开尔文公式为例

