无删失生存数据Wilcoxon秩和检验与logrank检验的比较*

南方医科大学公卫学院生物统计学系(510515) 陈 靖 何春拉 潘建红 陈平雁

生存数据通常可分为有删失和无删失两类。对于两组或多组生存时间的比较，存在删失数据时，logrank检验常作为首选方法;而无删失数据时，除logrank检验外，不少学者推荐用Wilcoxon秩和检验〔1〕。那么，对于无删失生存数据的比较，用logrank检验和Wilcoxon秩和检验哪种方法更好?这是应用中一个令人感兴趣的问题。为此，我们采用Monte-Carlo模拟方法〔2，3〕，旨在比较两种检验方法的统计性能，为此类数据处理提供依据。

模拟方法和结果

1.Ⅰ型错误率的模拟比较

(1)模拟方法及参数设置

比较Ⅰ型错误率时，从同一总体中独立抽取2个样本(模拟组数为2)，模拟 Weibull分布，Gamma分布，lognormal分布和 loglogistic分布4种分布情形〔4〕。参数设置:Weibull分布和Gamma分布下，设定刻度参数 λ1=λ2=1，形状参数 γ1=γ2=0.5;lognormal分布和loglogistic分布下，设定刻度参数μ1=μ2=1，形状参数σ1=σ2=0.5。所有假设检验均为双侧检验，检验水准为0.05。样本量n按照均衡设计考虑，分别取10、20、30、40、50、60…180、190 和 200。对每一种总体分布和样本量的组合，用SAS9.1.3软件〔5〕产生来自同一总体的两组独立的生存数据，每种组合的模拟次数均为10 000次，分别计算两种统计方法检验结果P＜0.05的次数在总的模拟次数10 000次中所占比例，即Ⅰ型错误率。

(2)模拟结果

图1为四种不同分布下，Wilcoxon秩和检验和logrank检验随样本量变化的Ⅰ型错误率。可见，Wilcoxon秩和检验的Ⅰ型错误率的曲线绝大多数情形在logrank检验的下方，尤以n≤50时两者的相差明显，个别情形两者重叠;此外，Wilcoxon秩和检验的Ⅰ型错误率基本上是在检验水准0.05的附近波动，且幅度不大。由此可见，logrank检验有扩大Ⅰ型错误率的风险，尤其在n≤50情形下。

2.检验效能(1-β)的模拟比较

(1)模拟方法及参数设置

比较检验效能时，从不同总体中独立的抽取2个样本;模拟 Weibull分布(γ=0.5)，Gamma分布(γ=1.5)，lognormal分布(σ =1)和 loglogistic分布(σ =0.5)4种分布情形，检验水准设为0.05。两组样本量n按照均2衡设计考虑，分别取10、30、50、70和100。设定刻度参数 λ1(或 μ1)为 0.5，λ2(或 μ2)分别取0.65、0.80、0.95、1.10 和1.25，则两总体差值(λ2- λ1或 μ1-μ2)分别为 0.15、0.30、0.45、0.60 和 0.75。每种组合模拟次数为10 000次，分别计算两种统计方法统计推断结果P＜0.05的次数在总的模拟次数10000次中所占比例，即检验效能(1-β)，并计算两种检验方法检验效能的相对比，以logrank检验的检验效能为参照。

(2)模拟结果

模拟结果见表1(Weibull分布和Gamma分布)和表2(lognormal分布和loglogistic分布)，当两总体差值一定时，Wilcoxon秩和检验与logrank检验都表现出检验效能随样本量增大而增大的趋势;样本量一定时，检验效能随两总体差值的增大而增大。

由表1见，Weibull分布和Gamma分布下两种统计方法的检验效能比值≤1，说明以logrank检验的检验效能较高，两者的差别以n≤50情况为甚。

由表2见，lognormal分布和loglogistic分布下两种统计方法的检验效能比值除了n=10外基本在1以上，说明除了n=10外以Wilcoxon秩和检验的效能较高。

图1 四种分布不同样本量下Ⅰ型错误率比较

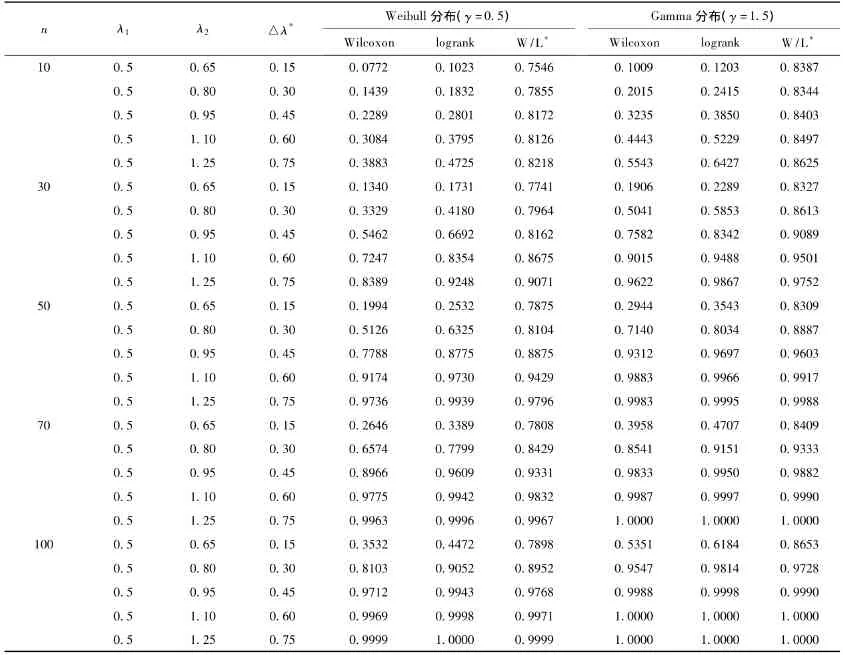
表1 Weibull和Gamma分布下两种方法检验效能比较

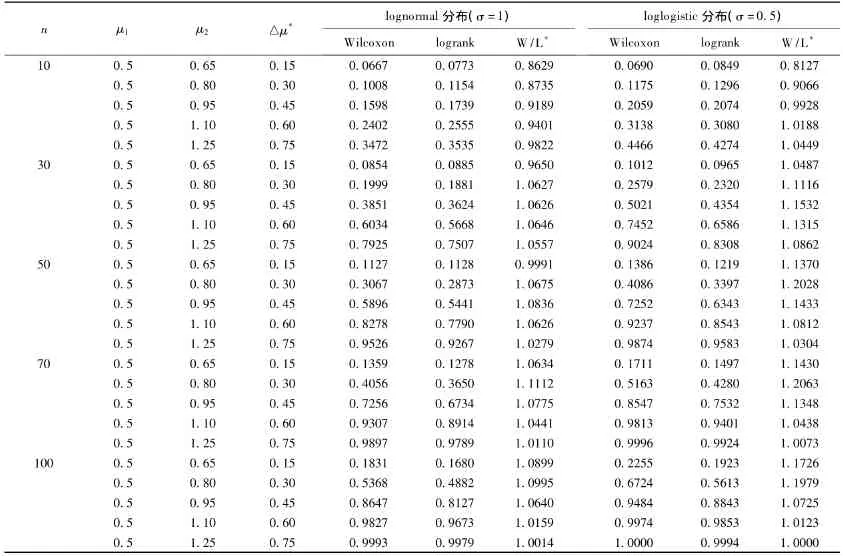
表2 lognormal和loglogistic分布下两种方法检验效能比较

讨 论

Ⅰ型错误率和检验效能是反映统计方法之性能是否优良的两个重要指标，Ⅰ型错误率越接近检验水准(本例取0.05)，检验效能越高，说明此种检验方法越可靠和稳健，效率越高。通常，对于Ⅰ型错误率和检验效能，我们首先考虑的是Ⅰ型错误率的控制，其次才是检验效能的比较。本研究模拟发现，在n≤50情形下，不论何种分布，Wilcoxon秩和检验的Ⅰ型错误率均小于logrank检验的Ⅰ型错误率，在接近检验水准的附近波动且幅度不大，说明logrank检验有扩大Ⅰ型错误率的风险。logrank检验是 Mantel(1966)对 Savage(1956)检验作出的推广〔6〕，是基于每个观测值均赋予一定的分值而制定出来的，这些分值是生存函数的对数的函数，与Wilcoxon秩和检验相比，更容易得到较大的检验统计量，从而导致较大的Ⅰ型错误率。对于两种统计方法的检验效能比较，在Weibull分布和Gamma分布下，以logrank检验较高;在lognormal分布和loglogistic分布下，以Wilcoxon秩和检验较高。综合来看，Wilcoxon秩和检验不仅Ⅰ型错误率控制得更好，而且在四种分布的两种分布中检验效能较高，应该说其统计性能较logrank检验优越。

早期Lee和Wang等曾提出当没有删失数据时，普通的非参数检验(如Wilcoxon秩和检验或Mann-Whitney检验)可以用于生存时间的比较〔6〕。而logrank检验是存在删失数据情况下对Savage检验作出的推广，且当比较的总体间风险函数比例近似不变时采用该检验较好〔7〕。Darilay(2011)〔8〕等人模拟了 n=20和n=50时3种分布(Weibull分布、lognormal分布和loglogistic分布)下，几种秩检验方法分析生存资料的Ⅰ型错误率和检验效能，当删失为0时，模拟结果与本研究相似。

综上所述，对无删失生存时间数据的比较，尤其是小样本情形(如n≤50)，我们建议采用Wilcoxon秩和检验。

1.Gibbons JD，Chakraborti S.Nonparametric Statistical Inference.4th Edition.New York:Marcel Dekker，2003，298-307.

2.Burton A，Altman DG，Royston P，et al.The design of simulation studies in medical statistics.Statistics in Medicine，2006，25(24):4279-4292.

3.Kroese DP，Taimre T，Botev ZI.Handbook of Monte Carlo Methods.New York:John Wiley and Sons，2011，301-343.

4.Kleinbaum DG.Survival Analysis:A Self-Learning Text.2nd Edition.New York:Springer，2005，263-286.

5.Delwiche LD，Slaughter SJ.The Little SAS Book:A Primer.3rd Edition.Cary:SAS Institute，2003，200-212.

6.Lee ET，Wang JW.Statistical methods for survival data analysis.3rd Edition.New York:John Wiley and Sons，2003，127-132.

7.Kalbfleisch JD，Prentice RL.The statistical analysis of failure time data.2nd Edition.New York:John Wiley and Sons，2002，20-23.

8.Darilay AT，Naranjo JD.A pretest for using logrank or Wilcoxon in the two-sample problem.Computational Statistics and Data Analysis，2011，