复杂抽样Poisson回归分析方法及应用*

胡跃华 匡翔宇 金承刚 Hasanat Alamgir 马林茂 冯国双 于石成△

最常见的复杂抽样是多阶段抽样，即在抽取样本时分为两个或两个以上阶段从总体中抽取样本的一种抽样方法。对这种采用多阶段抽样设计得到的数据，如果应用传统的统计方法分析数据而没有考虑由分层、整群及不等概率等因素所造成的设计效应变化，常常会导致统计推断的错误。主要体现在参数估计的标准误可能会被低估，估计的可信区间偏窄;假设检验的I类错误概率大于所规定的检验水准α〔1〕。

自1974年Kish和Frankel发表了针对复杂抽样调查数据的统计推断方法以来〔1〕，近年来复杂抽样调查数据的分析方法越来越受到关注〔2-3〕。大多数统计分析软件，如 SAS，SPSS，STATA和 SUDAN，将抽样权重纳入统计分析过程进行描述性统计、交叉表、复杂抽样一般线性模型和logistic回归等，使得复杂抽样调查数据分析应用越来越普及。

本文针对美国德克萨斯州行为危险因素监测系统(BRFSS)数据，探讨了45岁及以上的人群体重指数(BMI)与跌倒性伤害发生的联系;比较了复杂抽样Poisson回归与普通Poisson回归分析的结果，旨在阐述复杂抽样调查数据应用复杂抽样统计推断方法的必要性。

模型基本原理

复杂抽样Poisson回归也称调查加权Poisson回归，适用于用多阶段抽样技术得到的数据，如分层随机抽样或整群抽样。与普通Poisson回归一样，复杂抽样Poisson回归的反应变量作为一组解释变量的函数，要求在一定时间或空间上事件的发生独立、总体均数与方差相等以及观察结果有可加性;不同的是复杂抽样Poisson回归在统计推断时考虑了使用调查设计的信息来校正方差估计值〔4〕。反应变量表示在某一特定时间或空间发生的独立事件数目，它是一个非负的整数。事件发生数目这一随机变量服从Poisson分布:

λi是一定时间ti事件发生的“预期数或率”。Poisson回归模型应用“预期数或率”自然对数连接函数来构造与解释变量x的线性函数关系，如下:

xi是解释变量向量，β是参数向量，p为解释变量的数目。Poisson随机变量Yi的重要特性之一是其均数等于方差，即:

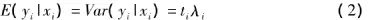
将式(1)进行对数变换，得:

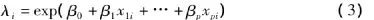
将(3)式代入(2)式，得:

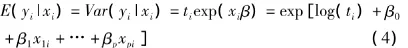
当构造应变量期望值E(yi|xi)的线性模型时，对式(4)应用自然对数连接转换，得到:

log(ti)为第i个个体观察时间的自然对数值，称为偏移量;上式为标准的Poisson回归模型。参数估计及检验:复杂抽样 Poisson回归参数估计构造一个加权Poisson伪似然函数(weighted Poisson pseudo-likelihood function)为:

采用牛顿-拉夫逊最大算法(Newton-Raphson maximum algorithm)使上述似然函数达到最大值的参数估计值，即是复杂抽样Poisson回归模型参数估计。复杂抽样Poisson回归参数假设检验用学生t检验，Stata提供了设计调整的Wald检验(design-adjusted Wald tests)进行多个解释变量参数的检验〔5〕。

Poisson回归整个模型的拟合评价采用Pearson卡方检验或偏差统计量及 Deviance残差图〔6〕。如果Pearson卡方检验统计量或偏差统计量与其自由度的比值等于1或接近1，P＞0.05，整个模型拟合优度好;如果Pearson卡方检验统计量或偏差统计量与其自由度的比值远大于1，说明计数数据间的变异较大，假定分布的均数与方差的关系不正确，Poisson回归不适合用来描述该数据，也称为过度离散(over-dispersion)。过度离散的控制可在模型中引入over-dispersion参数或采用负二项分布(negative binominal distribution)，负二项分布可处理资料不独立造成的过度离散，如具有传染性、地方聚集性、家庭聚集性(如乙肝)等疾病〔7-8〕。Deviance残差图一般用来比较两个回归模型的拟合优度，如Poisson回归和负二项回归;如果模型拟合较好，其残差绝对值在Deviance残差图中较小，有向0点收缩的趋势〔6〕。

Stata没有提供复杂抽样Poisson回归或负二项回归的拟合优度(goodness-of-fit)的Pearson卡方检验或偏差统计量及Deviance残差图〔9〕;可以用比较计数资料的模型分布和实际分布的图解技术方法来判断模型拟合优度，读者可参考Long和Freese的Stata程序完成比较〔10〕。但在拟合计数数据模型的时候，一个非常重要的步骤是确定Poisson回归和负二项回归哪个模型能更好地拟合数据。可在拟合一个复杂抽样Poisson回归模型后，再拟合一个有相同解释变量x的负二项回归，并计算负二项回归的离散参数α。Stata没有给出α的似然比检验，但输出α的点估计值和95%可信区间;如果α的95%可信区间包含0，表示可用复杂抽样Poisson回归拟合复杂抽样调查数据;否则改用复杂抽样负二项回归估计模型参数。

应用实例及结果解释

行为危险因素监测系统是美国CDC每年开展的行为危险因素电话调查，调查对象为年满18周岁及以上成年人，目前全美50个州都进行此项调查。由于BRFSS在样本选取时应用了抽取家庭电话号码的多阶段抽样，分析时要考虑电话号码选取概率不同、家庭中成年人数、家庭电话线条数和年龄性别的事后分层权重调整，将估计值调整到总体人群。因此，这种调整解决了每个人的抽样概率不等或样本对总体特征缺乏代表性的问题。

德克萨斯州BRFSS调查采用不成比例分层抽样(disproportionate stratified sample，DSS)设计。目标人群是德克萨斯州所有年满18周岁或以上的居民，且它们家庭的电话号码包括在用于抽样的电话号码簿里，即抽样框。将家庭电话号码分为两层，高使用频度和中等使用频度分别抽样，高使用频度的电话号码抽样概率大。抽到合格家庭后，如果家庭只有一个人且合格，则调查该人;如果有两个或以上合格的调查对象，则最近过生日的人为调查对象〔11〕。美国CDC已对德克萨斯州BRFSS数据计算出了每个个体的最终权重。

本报告应用2010年美国德克萨斯州BRFSS数据，分析跌倒后造成的伤害与体重指数的关系。因变量伤害定义为在过去的三个月内由于跌倒限制了至少一天的日常活动或去看了医生。自变量有体重指数(正常、超重、肥胖)、年龄(岁)、健康状况(中等和差、好和非常好)、性别、是否患有心血管疾病、婚姻状况、受教育程度、雇佣状况，其变量说明见表1。

BRFSS数据将在过去的3个月内发生1次或2次及以上跌倒性伤害作为反应变量，记为1，未发生任何跌倒性伤害为0，反应变量为二分类变量，可用复杂抽样logistic回归分析该数据，但这样分析损失了跌倒性伤害次数的信息。Poisson回归可处理计数的结果变量，加上本例跌倒性伤害发生率5.8%，可用复杂抽样Poisson回归分析数据。

SAS未提供拟合复杂抽样Poisson回归程序，分析用Stata完成。首先，设置复杂抽样设计，其Stata语句为:

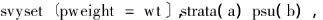
wt代表BRFSS数据库个体的最终权重，a表示数据库的分层变量，b说明数据库的群或基本抽样单位;这3个变量都需替换为BRFSS数据库里的相应变量名。Stata拟合Poisson回归、复杂抽样Poisson回归和复杂抽样NB回归语句:

injury为反应变量，其他为解释变量;在 bmi和health等解释变量前面的i指示该解释变量为分类变量，以哑变量的形式进入回归模型;irr要求输出RR值及其95%可信区间。

模型拟合策略:体重指数(正常、超重、肥胖)、年龄(岁)、健康状况(中等或差、好或非常好)、性别、是否患有糖尿病、是否患有心血管疾病、婚姻状况、受教育程度、家庭收入、雇佣状况、居住地点和种族12个变量作单因素复杂抽样Poisson回归分析，变量总的P值显示性别、居住地点、种族与跌倒性伤害无联系，将不纳入多因素分析的模型;从专业角度考虑，糖尿病与心血管疾病有共线性，将与跌倒性伤害联系强的心血管疾病纳入多因素分析模型中。分析超重、肥胖与跌倒性伤害的关联时，将年龄、健康状况、性别、心血管疾病、婚姻状况、受教育程度、雇佣状况作为调整变量放入模型，拟合普通Poisson回归、复杂抽样Poisson回归和复杂抽样NB回归模型，结果见表1。

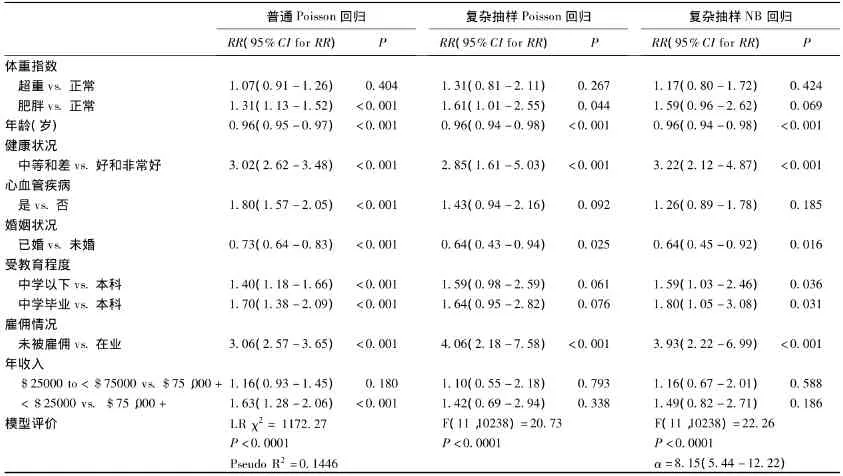
表1 普通Poisson回归、复杂抽样Poisson回归和复杂抽样NB回归拟合结果

对于复杂抽样Poisson回归或复杂抽样NB回归，目前Stata没有给出类似普通Poisson回归的似然比检验;只有应用复杂抽样NB回归计算离散参数，确定Poisson回归或NB回归哪个更适合描述数据。从表1的结果看，数据拟合负二项回归得离散参数为8.15，标准误1.68，α的95%CI=5.44-12.22，表明跌倒性伤害数据的方差是其均数的8.15倍，因此复杂抽样Poisson回归不适合拟合该数据，可应用复杂抽样负二项回归模型。普通Poisson回归分析与复杂抽样NB回归相比，前者高估了肥胖、患有心血管疾病、小于25000美元的年收入与跌倒性伤害的联系;低估了中等和差的健康状况、未被雇用与跌倒性伤害的联系;虽然也低估了已婚和受教育程度低与跌倒性伤害的联系，但拟合复杂抽样NB回归时，其P值小于0.05，而在普通Poisson回归中，P值小于0.001;年龄效应大小没用改变，其统计学假设检验结果也保持未变。

讨 论

在大型流行病学调查中多阶段抽样方法较简单随机抽样方法更经济有效，因此常常被使用。如将调查总体用某一特征(地理位置、经济状况、城市农村等)分为不同的层，然后从每一层里选取“群”(clusters of subjects)，再从选择的群里抽取一定数量的个体，同一“群”里的个体更具有相似性。对这种多阶段抽样得到的数据，如果用简单随机抽样的常规分析方法来分析复杂抽样的数据，因个体间的相似程度大，参数标准误估计通常会偏小。考虑“群”相似性特征的复杂抽样调查数据加权分析可产生更准确的标准误估计。

对于德克萨斯州BRFSS数据，普通Poisson回归分析结果显示:除超重vs.正常和年收入＜$25000 vs.$75，000+外，其他解释变量均有统计学意义。普通Poisson回归分析假设调查数据来自简单随机抽样(SRS)，这导致低估模型参数的方差和标准误，进而可信区间的估计变窄，致使统计推断受到影响，将无统计学意义判断为有统计学差异。如参数检验，普通Poisson回归估计的Z值偏大，P值偏小;作统计推断时，增加了I类错误的风险。

复杂抽样调查数据处理的理论和方法可追溯到100年前〔12-13〕，1945～1975年创立的复杂抽样调查的抽样设计、总体参数估计和统计推断仍是目前复杂抽样调查数据描述分析的基石。上世纪40年代后期，美国哥伦比亚大学社会学家Paul Lazarsfeld建立了复杂抽样调查数据测量变量间联系的分析方法，而不限于仅是总体特征的描述〔14〕。在1950～1990年随着新统计理论和方法的发展，复杂抽样调查数据的分析处理方法得到了更快的发展，包括列联表资料的对数线性模型和相关的方法、广义线性模型(logistic和Poisson回归)、生存分析、一般线性混合模型、结构方程模型和隐变量模型〔15〕，这些方法充分考虑了复杂抽样调查设计的样本特性，对参数估计的标准误和可信区间有更准确的估计。

目前，SAS 9.2已包含复杂抽样调查数据的描述(PROC SURVEYMEANS和 PROC SURVEYFREQ)、多元线性回归(PROC SURVEYREG)和logistic回归分析(PROC SURVEYLOGISTIC);但仍没有复杂抽样Poisson回归分析模块。Stata Version 13包含了描述分析、二分类结果(logistic回归和Probit回归)、有序结果(有序logistic回归和有序Probit回归)，多分类结果(多项式 logistic回归和 Probit回归)，计数结果(Poisson回归，负二项回归，零膨胀Poisson回归和零膨胀负二项回归)和生存分析等。SPSS最新版本除有基本的描述分析外，还有多元线性回归、二分类logistic回归、有序logistic回归和Cox回归分析等。SUDAN Version 9.0是一个很好的处理复杂抽样调查数据的统计分析软件，它包括描述性统计(PROC DESCRIPT，PROC CROSSTAB，PROC RATIO)、多元线性回归(PROC REGRESS)、二分类 logistic回归(PROC LOGISTIC/RLOGIST)、有序和多分类logistic回归(PROC MULTILOG)、Poisson回归(PROC LOGLINK)和生存分析(PROC KAPMEIER，PROC SURVIVAL)。除了上述分析复杂抽样调查数据四大软件外，其他统计软件如M-Plus，R，IVEware和WesVar等软件也具有复杂抽样调查数据统计描述和统计分析的功能，感兴趣的读者可参考有关书籍。

1.Kish L，Frankel MR.Inference from complex samples.Journal of the Royal Statistical Society，series B，1974，36:1-37.

2.Rao JNK.Interplay between sample survey theory and practice;an appraisal.Survey Methodology，2005，31:117-138.

3.刘建华，金水高.复杂抽样调查总体特征量及其方差的估计.中国卫生统计，2008，25(4):377-379.

4.Binder DA，On the variances of asymptotically normal estimators from complex surveys.Survey Methodology，1981，7:157-170.

5.Heeringga S，O'Muicheartaigh C，Survey Methods in Multinational Contexts.247-263.

6.楚慧珠，郜艳辉，邹宇华，等.负二项回归和Poisson回归在改水降氟效果中的对比分析.数理医药学杂志，2008，21(6):655-657.

7.刘亚杰，李海波，潘萍，等.朝阳市某高级中学结核病爆发的班级聚集性分析.中国卫生统计，2010，27(4):371.

8.薛付忠，王洁贞，马希兰.疾病空间分布状态的负二项分布概率生成模型的讨论.中国卫生统计，2000，17(6):366-368.

9.Heeringa SG，Alcser KH，Doerr K，et al.Potential selection bias in a community-based study of PSA Levels in African-American men.Journal of Clinical Epidemiology，2001，54(2):142-148.

10.Long JS，Freese J.Regression Models for Categorical Dependent Variables Using Stata.2nd ed，Stat Press，College Station，Texas，2006.

11.http://www.cdc.gov/brfss/.

12.Bowley AL.Address to the Economic Science and Statistics Section of the British Association for the Advancement of Science.Journal of the Royal Statistical Society，1906，69:548-557.

13.Fisher RA.Statistical Methods for Research Workers.Oliver and Boyd，Edinburgh，1925.

14.Kendall PL，Lazarsfeld PE.problems of survey analysis，in R.K.Merton and PF Lazaarsfeld(Eds.)，Continuities in Social Research:Studies in the Scope and Method of“The American Solders，”.Free Press，Chicago，1950.

15.Binder DA.On the variances of asymptotically normal estimation from complex surveys.Survey Methodology，1981，7:157-170.