转子 轴承系统油膜力特征的非线性动力学分析
刘桂珍,刘 杨,陈亚哲,闻邦椿
(1.东北大学 机械工程与自动化学院,辽宁 沈阳 110819;2.佳木斯大学 机械工程学院,黑龙江 佳木斯 154007)
对于大型高速转子系统,轴承的油膜力引起的转子运动失稳现象是突出问题,直接关系到机组的灾变防治和安全可靠运行[1].伴随着旋转机械不断向高速化、大型化发展,转子-滑动轴承系统的振动及稳定性对机械设备的性能具有越来越重要的影响.在转子-滑动轴承系统的动力学研究中,油膜不仅仅起着承受载荷、减轻摩擦、消除磨损、减振、抑制失稳及对轴承的冷却等作用,而且油膜的动态特性系数(油膜刚度系数和油膜阻尼系数)更是直接影响转子-滑动轴承系统动力学计算和稳定性分析[2-3].近年来,针对具有非线性油膜力的Jeffcott转子模型的弯曲振动进行研究,揭示了一些复杂的非线性动力学行为特征[4-5].这些非线性故障因素的存在使系统同频周期运动失稳后会产生较大的低频振动,其与同频周期运动叠加会使系统产生非谐调运动,转轴有交变应力的产生.转子失稳状态的长期存在导致的后果是很严重的.Rankine提出转子在一阶临界转速以下才能稳定运行的结论.JEFFCOTT H H以单圆盘挠性转子模型进行研究,得出转子在超临界状态下工作仍然稳定的结论[6].NEWKIRK B L等发现经过精密平衡的系统,转子仍会发生强烈振动[7].他还与TAYLOR对这种振动进行了实验研究,发现轴承油膜力是引起这种自激振动的原因.MUSZYNSKA A通过实验揭示了油膜涡动与振荡的动力学现象,描述了油膜涡动与振荡的特征[8].EHRICH F F通过实验证明,在高速涡轮机中发生过混沌运动[9].
本文根据30万kW汽轮发电机组模型试验台第一跨高中压转子的实际结构,建立了单跨双圆盘转子-轴承系统的转轴横向振动方程,其中采用了Ca-pone非线性油膜力模型.通过对该非线性系统进行数值分析,得出油膜力的形状及刚度与转速密切相关、油膜力显示出具有强非线性的结论.
1非线性油膜力作用下的转子 轴承系统的动力学模型
建立如图1所示的单跨双盘转子系统.为突出考虑非线性油膜力影响,在轴承轴颈处设集中质量,并将各段轴系质量等效到两圆盘中心及两轴承轴颈处;忽略扭转振动和陀螺力矩,只考虑转子的横向振动.
式中,Oxy为固定坐标系;Oi为回转中心(i=1,2,3,4);mi(i=1,2,3,4)为各轴承轴颈、圆盘集中质量;ki(i=1,2,3)为各段轴系横向刚度系数;ei(i=2,3)为圆盘质量偏心距;αi(i=3)为以圆盘O2为基准的质量偏心角.
对图1所示单跨双盘转子-轴承系统,建立其复坐标系下的运动微分方程:
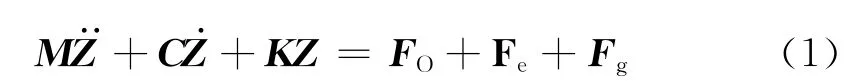
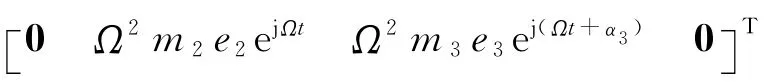
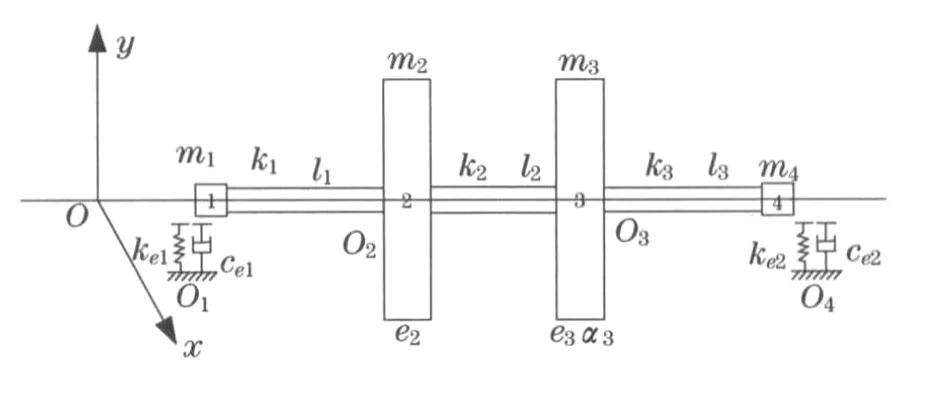
图1单跨双盘转子 轴承模型示意图Fig.1 Single span double plate of rotor bearing model schemes

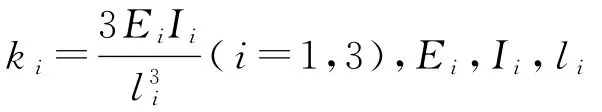
为方便计算转子系统油膜力,引入量纲一变换阵Δ=diag(δ1,δ1,δ4,δ4),δi(i=1,4)为轴承间隙.作变换τ=Ωt,可将式(1)化为量纲一形式为
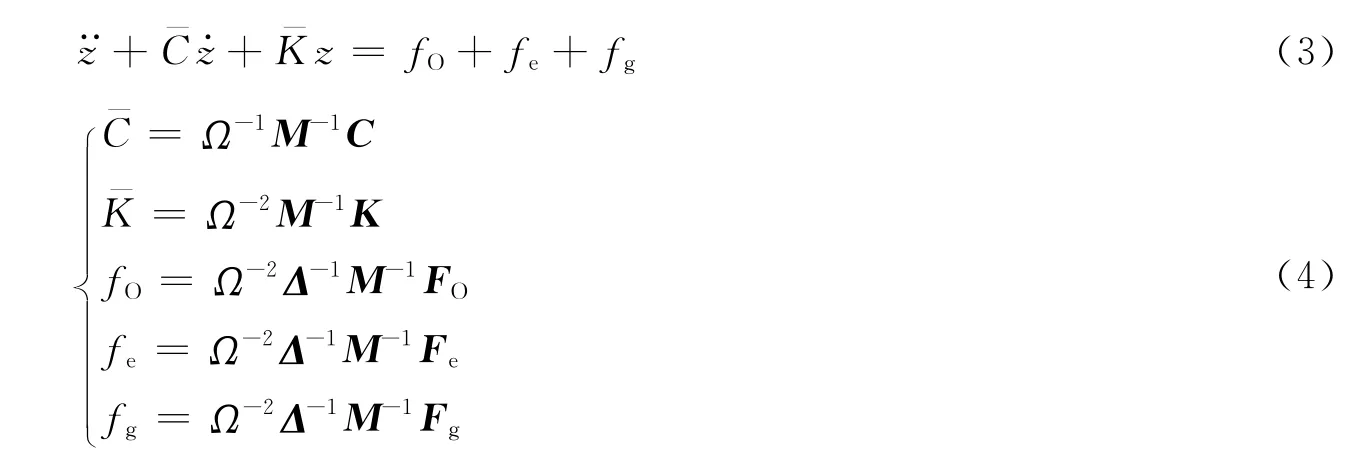
非线性油膜力模型采用短轴承假设下的Ca-pone非线性油膜力模型,该模型有较好的精度和收敛性.在短轴承油膜力假设条件下的量纲一化雷诺方程为
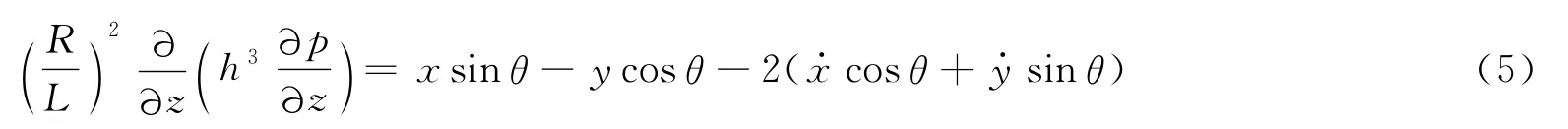
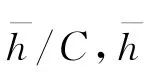
由式(5)可得量纲一油膜压力为

量纲一非线性油膜力最终可以表示为

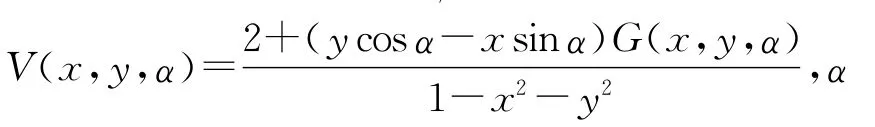
由此,可以得到复数形式的非稳态油膜力为


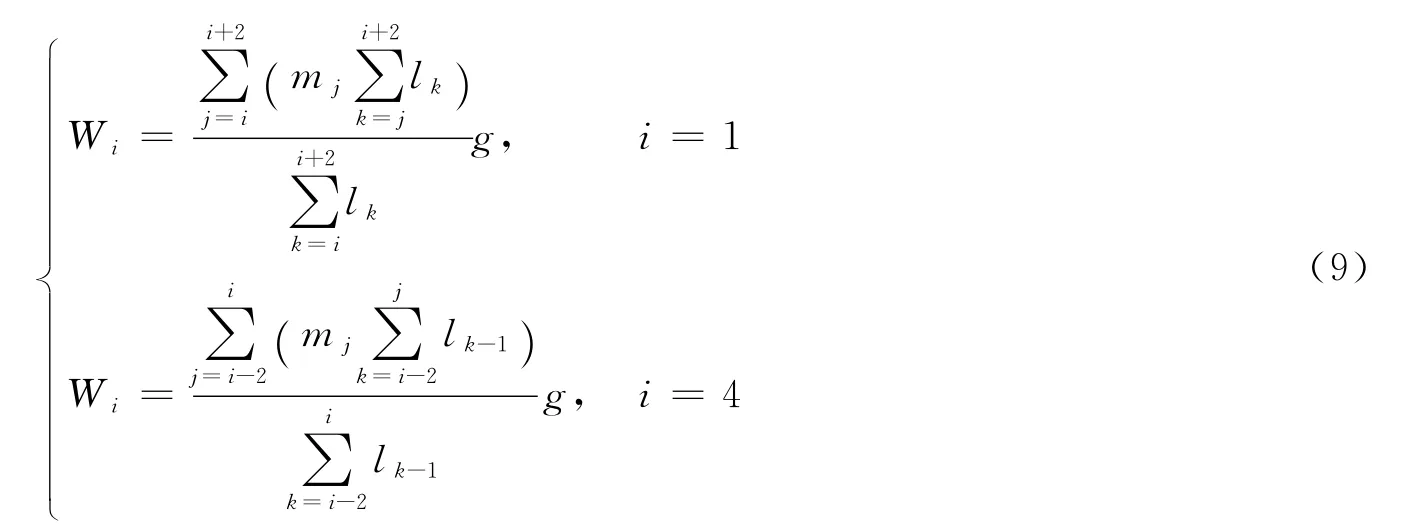
式中:lk为转子轴系各轴段的长度.
2 油膜力特征的数值仿真
取各圆盘质量为15.5kg,各轴段直径及长度参数分别为d1=30mm,l1=200mm,d2=32mm,l2=160mm,d3=30mm,l3=160mm,轴承间隙δ1,δ4为0.285mm,弹性模量E=2.06×105MPa.取两圆盘偏心均为0.1mm.这样两圆盘的振动相同,可以只分析一个.按上述数学模型,用数值方法求得系统转子随转速Ω变化时其对应油膜力的幅值变化如图2所示.
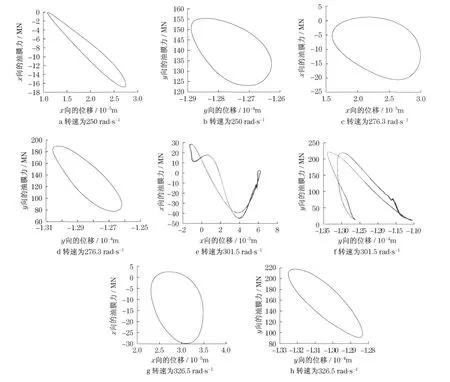
图2 不同转速下x,y方向的油膜力 位移曲线Fig.2 Different speed x,ydirection of oil film force the displacement curve
3 结论
从图2可以看出,油膜力的形状及刚度与转速密切相关,并且在升速过程中油膜沿x,y方向的刚度逐渐变大.在非共振区内油膜力-位移曲线呈滞回状特征;在共振区间,如图2e,f所示的油膜力-位移曲线,油膜刚度变化相对复杂,显示出油膜力的强非线性.
[1]闻邦椿,李以农,徐培民,等.工程非线性振动[M].北京:科学技术出版社,2007.
WEN Bangchun,LI Yinong,XU Peiming,et al.Engineering nonlinear vibration[M].Beijing:Science and Technology Press,2007.
[2]吴敬东,王娜,侯秀阴,等.非稳态油膜力下非线性刚度转子系统的碰摩故障分析[J].中国机械工程,2007,18(15):1850-1854.
WU Jingdong,WANG Na,HOU Xiuyin,et al.Unsteady oil film force nonlinear stiffness of the rotor system under the rubbing fault analysis[J].Chinese Mechanical Engineering,2007,18(15):1850-1854.
[3]黄文虎,武新华,焦映厚,等.非线性转子动力学研究综述[J].振动工程学报,2000,13(4):497-509.
HUANG Wenhu,WU Xinhua,JIAO Yinghou,et al.Nonlinear rotor dynamics research review[J].Journal of Vibration Engineering,2000,13(4):497-509.
[4]WAMG J K,KHONSARI M M.Application of hopf bifurcation theory to rotor-bearing system with consideration of turbulent effects[J].Graphology International,2006,39(7):701-714.
[5]陈子恕,丁千,孟泉.非线性转子的低频振动失稳机理分析[J].应用力学学报,1998,15(1):113-117.
CHEN Zishu,DING Qian,MENG Quan.Mechanism of suhsyn-chmnous vibration for a nonlinear rotor[J].Chinese Journal of Applied Mechanics,1998,15(1):113-117.
[6]JEFFCOT H H.The lateral vibration of loaded shafts in the neighborhood of a whirling speed the effect of want of balance[J].Phsophical Magazine Series 6,1919,37:304-318.
[7]NEWKIRK B L,TAYLOR H D.Shaft whipping due to oil action in journal bearings[J].General Electric Review,1925,28:559-568.
[8]MUSZYNSKA A.Whirl and whip-rotor/bearing stability problems[J].Journal of Sound and Vibration,1986,110(3):443-462.
[9]EHRICH F F.Some observations of chaotic vibration phenomena in high speed rotor dynamics[J].Transactions ASME Journal of Vibration and Acoustics,1991,113:51-60.
[10]ADILETTA G,GUXLO A R,ROSSI C.Chaotic motions of a rigid rotor in short journal bearings[J].Nonlinear Dynamics,1996,10(3):251-269.
——以匀加速直线运动公式为例

