基于Dirichlet过程的非参数贝叶斯方法研究综述

易莹莹

（南京邮电大学，南京 210046）

0 引言

贝叶斯方法通过利用现有的样本信息和某具体的先验信息来推导参数的后验分布，从而得出更为合理的推断。它是由英国学者T.贝叶斯的死后发表的一篇论文《论有关机遇问题的求解》最先提出，随着Jeffreys、Wald、Savage、De Finetti等贝叶斯学者对贝叶斯方法在观点、方法和理论上不断的完善，使得贝叶斯方法渐趋成熟。

在贝叶斯方法中，先验分布的选择是至关重要的，无论选择何种分布，都必须以合理性和计算的方便性作为选择标准。然而，目前并没有统一的先验分布构造方法，理想状态下，先验分布应该能够容纳主观地表达个人信念，但将其定量化并不容易，特别在高维情形下非常困难。一旦所作的假设或选择是不恰当的，就会得到不恰当的后验估计。由于很难在参数空间上找到恰当的先验分布，因此，有学者转而寻求非参数方法。Dirichlet过程是基于Dirichlet分布而生成的，虽然从Dirichlet过程抽取的分布都是离散分布，但是由于不能仅使用有限个参数对它进行描述，因而把它归类为非参数分布。

本文根据国内外的大量文献，对现有的基于Dirichlet过程的非参数贝叶斯方法进行了系统的综述，介绍了这一领域的最新进展，并讨论了进一步研究的方向。

1 基于Dirichlet过程的非参数贝叶斯方法研究

1.1 概述

非参数贝叶斯方法由Ferguson在1973年发表的一篇论文《A Bayesian Analysis of Some Nonparametric Problems》正式提出。基于Ferguson的观点，对于非参数问题，对先验分布有两方面的要求：（a）样本空间中，先验分布必须有足够大的支撑，甚至是包括空间中所有的分布。这就保证了先验选择的灵活性与广泛性，以便于找到最适合模型的分布函数。（b）在真概率分布中，给定样本观测值的后验分布必须易于分析。这就要求后验分布或者是共轭分布，或者是容易分析，从而保证在实际中的应用价值。然而这两个要求常常是相悖的。Ferguson证明Dirichlet过程满足这两个要求，且它具有一些优良性质。

设G是可测空间(ℜ,Ω)上的有限非零测度，Ω是由ℜ的子集构成的σ代数。令α是正实数，如果对任意j=1,2,…,k和ℜ的任意有限可测剖分(Β1,Β2,…,Βk)，随 机 向 量 (G(Β1),…,G(Βk)) 服 从 参 数 为(αG0(Β1),αG0(Β2),…,αG0(Βk))的 Dirichlet分布，将它记作(G(Β1),…,G(Βk))～Dir((αG0(Β1),αG0(Β2),…,αG0(Βk)))，那么 ，称G是 (ℜ,Ω) 上 的 Dirichlet过 程 ，记 为G～DP(α,G0)。Dirichlet过程的灵活性就在于它允许模型参数的实际先验分布G随机偏离基础测度G0。并且，Dirichlet过程的后验分布依然是Dirichlet过程这就使得其后验推断的计算比较易于分析。从直观上讲，它是先验分布G0和经验分布估计的加权平均，前者的权重为，后者的权重为很明显可以看出，当α→0时，Dirichlet的后验分布也就是其经验分布。

1.2 构造Dirichelt过程的方法

针对Dirichlet过程的诸多优良性质，有许多学者（Ferguson,1973;Blackwell&MacQueen,1973;Aldous,1985;Sethuraman,1994）提出构造Dirichlet过程的方法。

12.1 通过对Gamma过程一般化构造

既然可以用Gamma分布表示Dirichlet分布，那么同样道理，也可以利用Gamma过程来表示Dirichlet过程（Ferguson,1973）。Gamma分布 Γ(α,1)(α＞0)的特征函数为：（1）其中，现在定义一组新的变量J1,J2,…，它满足分布：

令式（1）中的α=α(ℜ)，P是 (ℜ,Ω)上的随机概率测度，(Β1,Β2,…,Βk)

是ℜ的任意可测剖分，那么有(P(B1),…,P(Bk))∈Dirichlet(α(B1),…,α(Bk))③Ferguson（1973）[17]给出了证明。证明如下：由于，则 Mj=(δVj(B1),…,δVj(Bk))服从独立多项分布 (Q(B1),…,Q(Bk))，且与具 有相 同 的 分 布 。 这 里 的是 Gamma 过 程 ，G(t)满 足因此，是独立随机变量，且有根据 Z是这些独立 Gamma 变量的和，所以有1，因此，P满足Dirichlet过程的定义。

1.2.2 使用波里亚罐子模型构造

许多概率分布可以通过使用罐子模型获得，对应Dirichlet分布的罐子模型是Pólya罐子模型（Blackwell&MacQueen,1973）。在有限域中，从Dirichlet分布抽样等价于产生一个Pólya序列。Blackwell&MacQueen证明这个结果可以扩展到无限域情形，从Dirichlet过程抽样等价于产生一个Pólya序列。

假设一个罐子中总共装了α个球，颜色为j的球最初个数为αj④这里假设αj是整数。（1≤j≤k）。现在每隔单位时间随机地从罐子中取出一个球后把原球放回，并同时加入一个与该球颜色相同的球。假设第i次从罐子中取出球的颜色为j的概率为p(Xi=j)，很容易知道有：

通过不断重复从给定X1,…,Xn-1下抽取Xn的过程构造序列X1,…,Xn-1的分布，令n≥1，有:

这个随机序列是无穷可交换的，即P(X1,…,Xn)=P(Xξ(1),…,Xξ(n))，符号ξ表示任意顺序。根据de Finetti定理⑤de Finetti（1935）定理：如果序列 y1,y2,…,yn是无穷可交换的，那么存在一个随机分布G，使得该序列服从独立同分布G：

，随机分布

P

(

G

)的先验分布是Dirichlet过程

DP

(

α

,

G

0

)，因此，这也就证实了Dirichlet过程的存在性。

1.2.3 使用中国餐馆过程构造

Dirichlet过程与中国餐馆过程紧密联系（Aldous,1985）。假设一个中国餐馆里有无数张桌子1,2,…，每张桌子能容纳下无数个顾客。进入餐馆中的每个顾客用i表示，第一个顾客1进入餐馆后选定第一张桌子坐下。第二个顾客2进入餐馆后要么会和第一个顾客坐在一起，要么会另选一张桌子坐下。……。第n个顾客会以的概率选择已经占有的桌子，其中c表示选择该桌子坐下的人数；以的概率选择另一张新桌子。α是此过程的标量参数，θi表示顾客i占有的桌子，每种座位排列构成一个剖分。

从上可以看出，任何两种座位排列只要它们包括相同的成份个数并且每个成份个数的大小相等，则这两种座位排列的概率相等。比如，有10个顾客进入一个餐馆，排列（1，3，8），（2，5，9，10），（4，6，7）⑥其概率为：和排列（1，4，6），（2，3，5，7），（8，9，10）⑦其概率为：的概率相等。因此，该序列是无穷可交换序列。根据de Finetti定理，也证实了Dirichlet过程的存在性。

如果将每张桌子看成是一个群，选择该桌子坐下的顾客看作是具有相同的取值，令所有的顾客表示为X1,…,Xn，将其中唯一的取值表示为X*1,…,X*m，具有该相同取值的顾客人数分别为n1,…,nm，那么，第Xn+1个顾客选择的预测分布为：

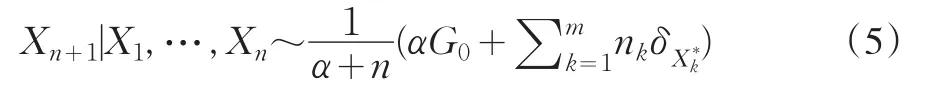
从式（5）中可以看出，nk越大，第Xn+1个顾客越有可能选择已选择过的桌子坐下，即越大的群越容易变大（richer-gets-richer）。这个构造表明Dirichlet过程具有“集群（clustering）”性质。

1.2.4 通过stick-breaking模型构造

Sethuraman（1994）给出了另一种Dirichlet过程的构造方法。假设某棍子单位长度为1。先在β1的长度将棍子折断，β1为刚刚折断的棍子长，剩下的棍子长为1-β1，然后每次将剩下的棍子以的长度折断，因此，在第i次折断后棍子的长度变为重复无穷次，由此构造的序列满足条件因此，我们可以定义随机测度G为：

Sethuraman证明用这个方法构造的随机概率测度G满足Dirichlet过程DP(α,G0)。

1.3 后验计算算法

尽管基于Dirichlet过程的非参数贝叶斯模型形式灵活，但是由于灵活所付出的代价是其计算相当复杂。这极大地阻碍了其发展，直至最近随着计算机性能的提高和计算算法的改进，该方法开始得到了广泛的应用。将其算法进行归纳可以分为两种，分别是蒙特卡罗抽样（MCMC sampling）算法和变分推断（Variational inference）算法。

1.3.1 蒙特卡罗抽样算法

由于蒙特卡罗算法可以获得模型的“精确”推断，它逐渐成为人们估计Dirichlet过程的首选。利用蒙特卡罗算法计算需要建立马尔可夫链对未知变量进行抽样模拟，当马尔可夫链达到稳态分布时即得到所求的后验分布。它实现了由计算机从后验分布模拟抽样然后用样本估计值来推断总体特征，其基本思想是：依据马尔可夫链性质，从条件后验概率分布中连续抽取出多组样本，则这些样本最后将会各自收敛到某种分布，由这些模拟的抽样值计算的各种特征值，如期望值、方差等，可直接用来描述各该参数后验概率分布的特征，而不必再通过多重积分求解边际后验概率分布。于是，如何基于蒙特卡罗的稳态分布从概率密度函数中抽样，成为运用蒙特卡罗算法的关键。

Escobar（1994）和 Escobar&West（1995）提出波里亚罐子Gibbs抽样法（Pólya urn Gibbs sampler），虽然该方法能产生一条遍历的马尔可夫链，但是该链收敛于稳定分布的速度会很慢，这是由于许多观察值可能会具有相同的分布值。为此，MacEachern&Müller（1998）提出加速波里亚罐子Gibbs抽样法（accelerated Pólya urn Gibbs sampler），该方法能提高抽样效率，但是它只适用于先验分布是共轭分布情形。Neal（2000）在MacEachern&Müller的研究基础上，将先验分布扩展到了非共轭情形，当增加的变量个数为1时，它等价于MacEachern&Müller（1998）中的“no gaps”算法。其它研究包括Bush&MacEachern（1996）、Walker&Damien（1998）、Ishwaran&James（2001）、Green&Richardson（2001）、Dahl（2005）、Jain&Neal（2007）、Dahl et al.（2008）等等。在最新的研究中，Papaspiliopoulos&Roberts（2008）和 Walker（2007）分别提出了回顾抽样（retrospective sampling）和切片抽样（slice sampling），这两种方法都是基于条件增加（conditional augmentation）的基础上，使得复杂的多层结构变得更加灵活，抽样结果更加精确。蒙特卡罗算法的不足之处是其抽样速度比较慢，特别对于大量高维数据。

1.3.2 变分推断算法

变分推断算法广泛应用于渐进概率的推断。它的基本思想是使用Jesen不等式⑧对于可观察变量x和隐变量h，Jesen不等式是指：来得到对数似然函数的一个可变下界。本质上说，就是使用带索引的变分参数得到一个下界函数族，然后通过使两者的KL距离最小，从而得到一个最紧的下界。Blei&Jordan（2006）和Kurihara et al.（2006）提出了stick-breaking变分推断算法。Wang&Blei（2009）在前人基础上提出了嵌套中国餐馆变分推断算法。这些学者发现变分推断算法使用易处理的一簇分布来逼近模型中间隐变量的后验分布，从而一方面能够加快计算速度，另一方面可以避免最大似然估计的参数奇异问题。但与蒙特卡罗算法相比，它的缺陷是其抽样结果的精确度要更差些。

2 未来发展方向

目前，Dirichlet过程在贝叶斯统计和机器学习中都是研究的热门领域。它放松了先验分布为参数分布的限制，将先验分布扩展到了非参数分布，从而使得后验分布的推断更为灵活。它正处于不断发展研究的阶段，还有许多问题可以进行拓展分析，主要体现在以下几个方面。

（1）改进计算算法。如前所述，蒙特卡罗抽样算法的精确度较高，但是抽样速度较慢，而变分推断算法虽然速度较快，但是精确度不太高。因此，设计出一种既能在精确度方面也能在抽样速度方面都改进的算法是值得深入分析的问题。

（2）扩展非参数先验分布Dirichlet过程。比如对Pitman-Yor过程、层级Dirichlet过程（hierarchical Dirichlet process）、嵌套Dirichlet过程（nested Dirichlet process）、印第安蝴蝶过程（Indian buffet process）以及依赖Dirichlet过程（dependent Dirichlet process）等等的分析，使得非参数贝叶斯估计方法更加的完善。

（3）应用非参数贝叶斯方法。目前非参数贝叶斯方法的应用研究领域主要是密度估计、分层线性模型、有序数据以及生存数据的分析。除了进一步在这些领域进行深入分析以外，还可以将其应用于探索聚类分析、空间统计估计、分位回归估计等等。

3 结语

非参数贝叶斯估计方法结合了贝叶斯方法和非参数方法的许多优点，既充分利用样本信息，又将一些信息不充分的变量纳入模型，因而，它可以充分描述和概括模型的特点，随着计算算法的提出和计算技术的提高，它的研究具有广阔的前景。

非参数贝叶斯估计方法有着广阔的理论研究和实际应用前景，其研究才刚刚起步，但它自出现以来一直是相关领域的研究热点，相关的非参数过程以及新的算法是近年来的研究重点。非参数贝叶斯方法具有许多优势，能够解决更复杂的问题。本文综述了非参数贝叶斯方法的发展，并说明了其未来研究的关键问题和发展方向。

[1]茆诗松.贝叶斯统计[M].北京：中国统计出版社，2005．

[2]Kotz&吴喜之.现代贝斯统计学[M].北京：中国统计出版社，2000．

[3]Ferguson,T.A Bayesian Analysis of Some Nonparametric Problems[J].The Annals of Statistics,1973,1(2).

[4]Blackwell,D.,MacQueen,J.B.Ferguson Distribution via Pólya urn Schemes[J].The Annals of Statistics,1973,（1）.

[5]Aldous,D.J.Exchangeability and Related Topics.In P.-L.Hennequin(ed.),Ecole d É té de Probabilités de Saint-Flour XIII.Lecture Notes in Math.1117[M].Berlin:Springer-Verlag,1999.

[6]Sethurman,J.A Constructive Definition of Dirichlet Priors[J].Statisti⁃ca Sinica,1994,（4）.

[7]Doss,H.Bayesian Nonparametric Estimation for Incomplete Data Via Successive Substitution Sampling[J].Annals of Statistics,1994,（22）.

[8]Muliere,P.,Tardella,L.Approximating Distributions of Random Func⁃tional of Ferguson Dir-ichlet Priors[J].Journal of Statistics,1998,26(2).

[9]Geweke,J.Evaluating the Accuracy of Sampling-based Approaches to Calculating Posterior Moments[M].Oxford:Clarendon Press,1992.

[10]Escobar,M.D.Estiamting Normal Means with a Dirichlet Process Pri⁃or[J].Journal of the American Statistical Association,1994,（89）.

[11]Escobar,M.,West,M.Bayesian Density Estimation and Inference Us⁃ing Mixture[J].Journal of the American Statistical Association,1995,90(7).

[12]MacEachern,S.N.Estimationg Normal Means with a Conjugate Style Dirichelt Process Prior[J].Communications in Statistics:Simulation and Computation,1994,（23）.

[13]MacEachern,S.N.Müller,P.Estimating Mixtures of Dirichlet Process Models[J].Journal of Computational and Graphical Statistics,1998,7(6).

[14]Müller,P.,Quintana,F.Nonparametric Bayesian Data Analysis[J].Sta⁃tistical Science,2004,19(1).

[15]Neal,R.M.Markov Chain Sampling Methods for Dirichlet Process Mixture Models[J].Journal of Computational and Graphical Statistics,2000,9(2).

[16]Bush,C.A.,MacEachern,S.N.A Semiparametric Bayesian Model for Randomized Block Designs[J].Biometrika,1996,（83）.

[17]Walker,S.,Damien,P.Sampling Methods for Bayesian Nonparametric Inference Involving Stochastic Processes[M].New York:Springer-Ver lag,2001.

[18]Ishwaran,H.,James,L.F.Gibbs Sampling Methods for Stick-breaking Priors[J].Journal of the American Statistical Association,2001,（96）.

[19]Green,P.J.,Richardson,S.Modelling Heterogeneity with and without the Dirichlet Process[J].Journal of Statistics,2001,（28）.

[20]Dahl,D.B.Sequentially-allocated Merge-split Sampler for Conju⁃gate and Nonconjugate Diric-hlet Process Mixture Models[J].Jour⁃nal of Computational and Graphical Statistics,2005,(11).

[21]Jain,S.,Neal,R.M.Splitting and Merging Components of a Nonconju⁃gate Dirichlet Process Mixture Model[J].Bayesian Analysis,2007,2(3).

[22]Dahl,D.B.Mo,Q.,Vannucci,M.Simultaneous Inference for Multiple Testing and Clustering Via a Dirichlet Process Mixture Model[J].Sta tistical Modelling,2008,8(1).

[23]姚宗静.基于Dirichlet过程的非参数贝叶斯分析[D]成都：西南交通大学，2007．

[24]Papaspiliopoulos,O.,Roberts,G.O.Retrospective Mcmc for Dirichlet Process Hierarchical Models[J].Biometrika,2008，(95).

[25]Walker,S.Sampling the Dirichlet Mixture Model with Slices[J].Comm.Statist.Sim.Comput，2007，(36).

[26]Blei,D.,Jordan,M.Variational Inference for Dirichlet Process Mix⁃tures[J].J.Bayesian Anal，2006，（1）.

[27]Kurihara,K.,M.Welling,N.A.Vlassis.Accelerated Variational Dirichlet Process Mixtures[Z].In NIPS，2006.

[28]C.Wang,D.Blei.Variational Inference for the Nested Chinese Res⁃taurant Process[Z].Neural Information Processing Systems,2009.

[29]Ghahramani,Z.Nonparametric Bayesian Methods[EB/OL].http://www.gatsby.ucl.ac.uk,1998.