中国通货膨胀预测:基于AR和VAR模型的比较
张卫平
(复旦大学 经济学院,上海 200433)
0 引言
通货膨胀率是宏观经济最重要的指标之一。对通货膨胀率做出准确可靠的预测不仅是政府政策部门和中央银行宏观经济决策的重要依据,而且也是企业和居民经济活动以及预期形成的重要参考。随着计量经济学在时间序列方面的发展,已经有了一系列可以选择的模型来预测通货膨胀。在形形色色的模型当中,究竟哪类模型对通胀的预测更加准确呢?考虑一定“结构”的模型能够胜过简单的随机游走式的预测吗?货币量或者GDP(名义的或者实际的)可以改善通胀的预测精度吗?这些问题,都是关于通货膨胀预测有待寻求答案的问题。
本文将利用中国1996Q1~2010Q2的季度数据,分析两类最基本的时间序列模型——AR模型和VAR模型在预测中国通胀上的表现,以弥补国内研究的不足。我们重视基本模型,是因为,既然连最简单的随机游走模型都有可能在通胀预测方面击败其他复杂模型,我们没有任何理由忽视简单的基本模型的预测能力。有关通货膨胀预测的实证研究有必要回归简单的基本模型,认真和系统地分析它们对通货膨胀的预测能力,而不是仅仅偏好复杂的“花哨”模型。
1 模型预测能力的评价标准
本文用πt表示季度通货膨胀率(年率),即πt=400ln,其中,P为CPI定基指数。用表示到t期为止前h期的平均通胀率(年率),即用πt+h|t表示在t期对t+h期通胀πt+h的预测,用表示在t期对t+1到t+h期共h期的“平均通货膨胀率”的预测。当h=1时,;当h>1时,可以有两种方法得到样本为T的样本外预测一种是直接法,即直接把作被解释变量建立模型,直接通过模型方程计算另一种是间接法,即把πt+1做被解释变量建立模型,在得到1步向前样本外预测πT+1|T之后,可以通过迭代方法得到样本T之外其它期的预测πT+s|T,s>1。然后计算πT+1|T到πT+h|T共h期的平均值,即可得到本文采用第二种方法。
本文利用样本外预测表现来作为评价模型预测能力优劣的标准。在整个样本区间通过一定的方法构造多个子样本,对每个子样本,都可以对给定模型的参数进行估计,并利用模型对子样本外的观测进行预测,然后比较该预测值与该子样本外观测的真实值。为了评估某类模型的预测能力,我们将考虑该模型下所有子样本集合的预测值与真实值之间的“平均”误差。
对时间序列数据而言,有两种较为常用的构造子样本的方法:迭代法和滚动法。迭代法固定样本窗口左边界,并通过移动窗口右边界来改变样本;滚动法固定样本窗口的宽度,通过移动窗口的位置(同时改变窗口的左边界和右边界)来构造不同的样本。本文将同时考虑两种方法。每种方法下,当窗口右边界从t1移动到t2时,我们可以得到(t2-t1+1)个预测值,然后计算均方根误(RMSE),其数学形式为

本文通过比较不同模型的RMSE来比较不同模型的预测能力。
2 模型选取、估计以及预测方法
我们认为在研究清楚“简单”模型对中国通胀的预测方面的表现之前,放弃较为复杂的模型是研究的正常道路。本文做出的这种模型选择除了是因为这两类模型是非常基本和重要的时间序列模型之外,也是因为它们通常被认为是预测效果较好的模型,而且易于进行参数估计(只需要线性优化,比如最小二乘,而不需要非线性优化方法)。借助于这两类模型,本文试图回答如下问题:(1)AR类模型和VAR类模型在预测中国通货膨胀方面,是否能够胜过简单随机游走模型么;(2)引入其他变量的VAR模型能否改善单变量AR模型的预测效果么;(3)VAR模型中,引入不同变量的预测效果有什么差异,什么变量的效果最好;(4)在这两类模型中,哪种具体形式的模型在通胀预测方面表现最好。
除了AR和VAR模型外,本文在实证部分对各种模型的预测能力进行比较和评价的过程中,采用的基准预测模型是最为简单的随机游走模型,即下期通胀预测值就等于当前期的通胀率,对于本文的季度数据而言,即

下面,我们对AR和VAR模型进行简要的说明,并对后文实证部分用到的的参数估计和变量预测方法进行简要的描述。
2.1 AR模型:设定、估计和预测
本文考虑的第一类模型为AR模型,它的形式如下
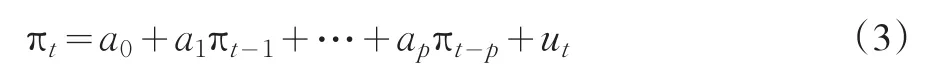
其中πt为通货膨胀率,本文选择的是剔除了季节性的定基比的消费者价格指数的对数差分;πt-1,…,πt-p是滞后1期到滞后p期的通货膨胀率;ut为t期的扰动项;a1,…,ap为p个AR参数,a0为常数项。
对式的估计可以用最小二乘(OLS)法,即对每个给定的用于参数估计的子样本,我们把前p个观测用于构造πt-1,…,πt-p,剩余的部分作为被解释变量,用π表示。假定数据长度为T,时间起止为[t1,t2]。令Z=[πt-1,,它是(T×p)维矩阵。用(p+1)维列向量a表示参数集合,那么参数a的OLS估计量为

由于本文关注的只是各种模型预测的样本外表现,不涉及单个预测的标准差问题,所以这里不讨论扰动项ut的分布假定或者参数估计量的分布。给定子样本,得到参数的估计值之后,可以形成对该子样本之外的一步预测,即对第一个通货膨胀率πt2+1的预测,其值为

通过递归方法,可以得到2步预测πt2+2|t2,3步预测πt2+3|t2,……,直到h步预测πt2+h|t2。根据前文,我们可以根据1步到h步的预测值计算在t2期对未来1至h期的通胀预测,并计算其与真实值的误差。通过改变[t1,t2]区间,我们可以得到误差序列,并根据式计算RMSE。对任何给定的p的具体模型,都可以计算该模型的RMSE。
2.2 VAR模型:设定、估计和预测
本文考虑的第二类模型为VAR模型,该模型自Sims(1980)以来,被广泛应用于宏观经济中的实证研究,这里用它来考虑通货膨胀预测问题。VAR模型的具体形式为

其中,π与上面讨论的AR模型一样,表示通货膨胀率;A1,…,Ap为p个VAR参数矩阵;A0为常数项矩阵,(本文用符号“|”表示变量的串联)为扰动项向量,其中et对应πt方程,vt对应xt,或者为标量或者为向量;x表示其他某个变量或者由其他变量组成的向量,本文考虑如下变量,名义GDP增长率(DNGDP)、实际GDP增长率(DRGDP)、货币供给增长率(DM0、DM1、DM2)、生产者价格指数衡量的通货膨胀率(DPPI)。它们或单独进入x,此时该变量和π构成两变量VAR系统;或每次选取两个进入x,此时该变量对和π构成三变量VAR系统。对于每个具体模型(包括滞后阶数),我们都将进行参数估计、预测以及RMSE的计算。
用yt表示方程的左边,即它为K维列向量。用表示方程右边的扰动项向量,它也是K维列向量。采用Lütkepohl(2006)的符号表示方式:

模型可以写为

参数A的OLS估计量为

同样,这里不讨论参数的分布。给定子样本区间[t1,t2],可以得到参数估计值,然后就可以对yt中的变量进行一步预测,即对yt2+1的一步预测为

yt2+1|t2的第一个元素即为通货膨胀率的一步预测πt2+1|t2,同AR模型一样,我们可以用递归方法计算2到h步预测,并得到t2期对未来1至h期的通胀预测,变动样本,最终可以得到该具体VAR模型的RMSE。
3 数据及其简单的统计性质
本文的全部变量的数据总样本区间为1996Q1~2010Q2,数据频率为季度。数据起点选择1996年,是因为从1996年起,狭义货币M1和广义货币M2正式成为货币政策的调控目标,这种统一的制度环境,使得我们在分析货币量是否有助于改善通胀预测时,可以避免受制度环境变化的影响;同时也便于在与单变量的模型进行比较时,有个统一的时间范围,这使得我们不去分析更长时间范围的单变量模型,即便CPI度量的通胀数据可以获得更长的序列。我们用CPI指数计算得到的通货膨胀率作为本文预测的对象。其中的CPI指数以2005年1月为基期,利用2005年其他月份的月度环比以及其他年份的月度同比,可以计算月度CPI定基指数;选取每个季度最后月份的月度CPI定基指数,可以得到季度CPI指数,用P表示,然后计算得到通货膨胀率选取每季度最后一个月的货币量作为季度货币量数据,可以构造货币量增速利用季度的名义GDP数据可以构造名义GDP增速DNGDPt=400ln(NGDPt/另外,根据国家统计局公布的GDP实际同比增速,我们可以构造GDP定基比指数,根据此指数可以构造实际GDP增速全部数据均用X11方法剔除了季节性因素。对这些变量的简单统计性质的描述见表1。
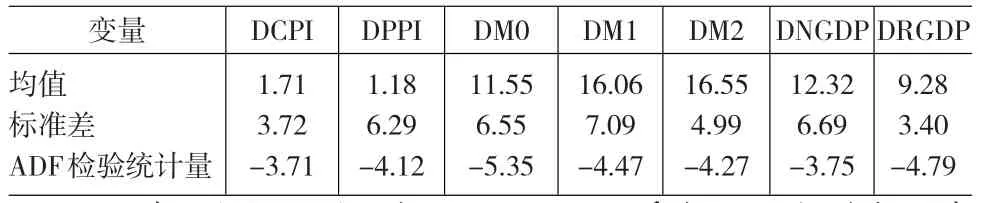
表1 简单统计描述和ADF单位根检验
用CPI度量的通货膨胀是否含有单位跟,是进行通货膨胀预测首先会考虑到的问题。这将帮助我们决定,在构建通货膨胀预测模型时,是直接对通货膨胀本身建模,还是对一阶差分后的通货膨胀进行建模。另外,在本文考虑的VAR模型中,其他变量是否平稳也是我们关心的数据特征。表1最后一行给出了本文用到的变量的时间序列的ADF单位根检验的t统计量值。由于所有的时间序列都没有明显的确定的一阶时间趋势,所以检验都采取只含有常数项的检验形式,所有检验统计量的值均在1%的显著水平上拒绝原序列含有单位根的零假设(本文没有给出临界值)。因此我们直接对通货膨胀水平,而不是通货膨胀的差分建模。
4 实证结果
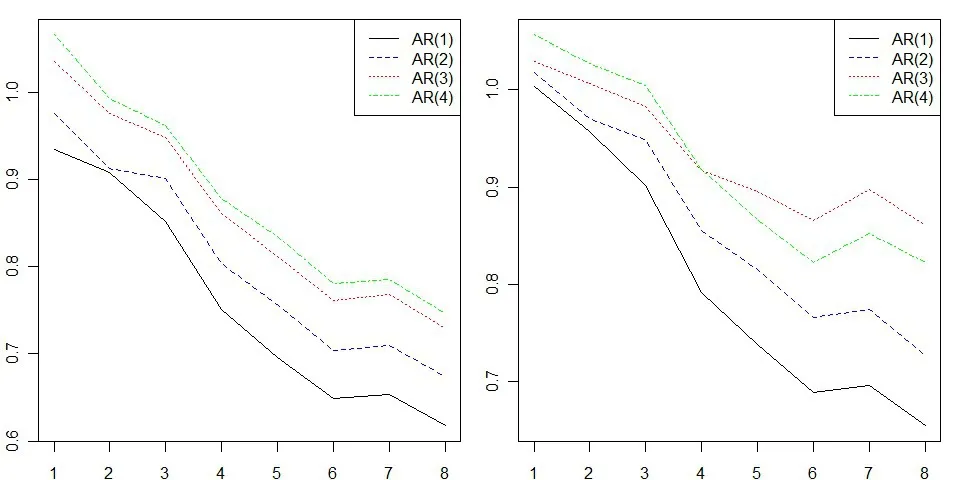
图1 AR模型在不同p和h下的相对RMSE
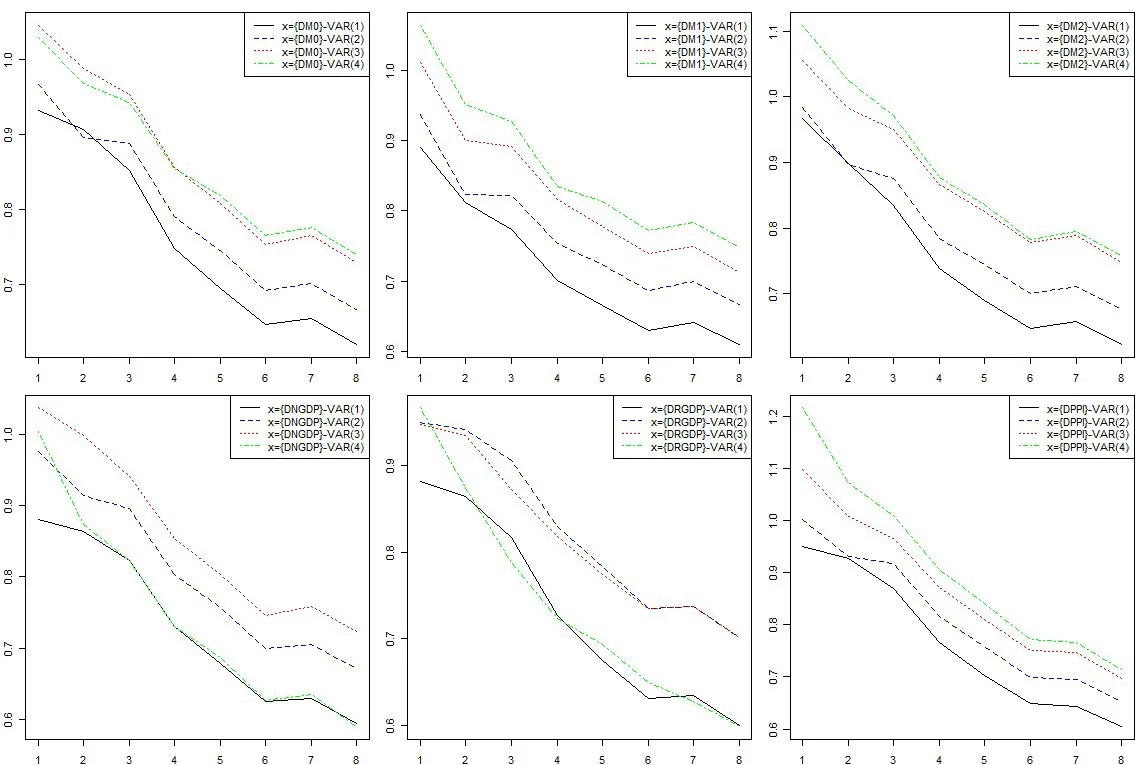
图2 两变量VAR模型在不同p和h下的相对RMSE(基于递归方法)

图3 两变量VAR模型在不同p和h下的相对RMSE(基于滚动方法)

图4 三变量VAR模型在不同p和h下的相对RMSE(基于递归方法)
为了更清楚地说明在预测中国通货膨胀方面,各种模型的预测能力,本文将分几个方面来总结实证结果。我们首先考虑AR和VAR模型中选择不同滞后阶数p以及在不同预测期h上的表现;其次考虑两变量和三变量VAR模型中,随着x变量选取的不同,模型之间的预测能力的比较。图1~图5包含了本文全部实证结果的信息。图6~图8则是为了模型比较的方便,对实证结果从特殊视角的展示。所有的图形横轴坐标均表示h,即预测期,本文h的取值范围为1~8,这相当于一个季度到两年。纵轴坐标都是不同模型的RMSE的相对于参考模型的RMSE的比值,其中图1~图5参考模型为随机游走模型,图6、图7参考模型为AR(1),图8参考模型为包含M1增速的两变量滞后1阶的VAR模型。

图5 三变量VAR模型在不同p和h下的相对RMSE(基于滚动方法)

图6 两变量VAR模型x变量不同选择下与AR(1)的相对RMSE

图7 三变量VAR模型x变量不同选择下与AR(1)的相对RMSE

图8 三变量VAR与两变量VAR模型的比较
4.1 不同滞后阶数以及预测期的比较
从图1~图5可以看出,绝大部分具体形式的模型在绝大部分的预测期上都优于简单的随机游走式的预测,即纵轴的值大都小于1;而且预测期越长,AR或者VAR模型相对于随机游走式的简单预测的优势就越明显,即随着h的增加,纵轴的值倾向于减少。大部分情况下,滞后阶数越少,模型的表现越好,这符合AR和VAR模型在预测方面的一般特征。下面给出各个图形其他方面的具体表现或者特殊情况。
图1是单变量AR模型预测表现的汇总,其中左图为递归方法下的结果,右图为滚动方法下的结果。AR模型在预测未来一个季度的通胀上,对随机游走模型的优势并不明显,左图中只有AR(1)和AR(2)模型的RMSE略低于随机游走模型的RMSE;右图,所有1至4阶的AR模型的表现均不如随机游走模型。但在2~8个季度上,除了滚动方法下的个别形式的AR模型,包括AR(3)模型在h=2时的预测、AR(4)模型在h=2,3时的预测,剩余所有形式的AR模型的表现均优于随机游走模型。
图2和图3是两变量的VAR模型在递归方法和滚动方法下的表现。通货膨胀π始终是两个变量之一,两变量的另一个变量x则有不同选择。这里,含有名义GDP增速和实际GDP增速的模型表现稍微有些特殊,此时的VAR(4)虽然仍旧不如VAR(1),但大部分情况下优于VAR(2)和VAR(3),这有可能是因为产出对历史产出的依赖性更强,也有可能是数据在进行季节调整时,调整过度或者不足②本文更多关注的是“典型”特征,对这种近似于个案的情况不做深入。。
图4和图5是三变量VAR模型在递归方法和滚动方法下的表现。π依然是三变量中必选的一个。另外两个变量,一个是货币量增速(DM0或DM1或DM2),另一个是产出增速(DNGDP或DRGDP)。由于PPI信息在预测通胀方面较差的表现,我们在三变量VAR模型中,不考虑PPI度量的通胀率。总的来说,滞后1阶的VAR表现最好。在基于递归方法下的结果中,VAR(4)虽大部分情况不如VAR(1),但通常比VAR(2)和VAR(3)要好。
4.2 VAR中x变量不同选择的比较
为了更清楚地比较VAR模型中x的不同选择对模型预测能力的影响,我们只关注表现最好的滞后阶数为1的模型。用图6和图7来分别比较两变量VAR(1)模型和三变量VAR(1)模型各自内部的比较,与图1~图5不同,这里参考模型为AR(1)。用图8来看在x为DM1时,引入DNGDP或者DRGDP的是否能进一步改善预测精度。
从图6可以看出,引入额外的信息,未必会改善对通胀的预测。能否改善单变量中表现最好的AR(1)的预测精度,取决于所选变量是什么。如果x是DM1或DNGDP或DRGDP,那么该变量带来的额外信息将有助于提高通货膨胀的预测精度;反之,如果x是DM0或者DM2或者DPPI,那么引入额外信息,基本不会改善AR(1)的预测精度。如果一个拥有历史通胀数据的人被允许可以另外选择一个变量,以便对未来通胀做出预测,那么这个人会考虑他要预测多久的通胀,如果是未来一个季度,那么他最优的选择是名义GDP或者实际GDP;如果是2~5个季度,那么最优的选择是M1;如果更长期的,比如两年,那么他的最好选择是名义GDP;无论多长时期的通胀预测,额外拥有M0、M2或者PPI数据,不会帮助他得到基于历史通胀数据本身得到的结果更好的预测。
从图7可以看出,三变量模型中,M1的表现依然优于M0和M2,M1无论与名义GDP还是实际GDP组合,其中包含的信息对预测通胀而言,都是三种货币量中表现最优的。在与M1的组合中,另一个变量是名义GDP增速在大部分情况下要比另外一个变量是实际GDP增速要有更好的表现。
从图6和图7可以知道,单独引入DM1的VAR模型,或者同时引入DM1和产出增速(DNGDP或DRGDP)的VAR模型,都可以改善仅借助于历史通胀的AR(1)预测。我们很容易想到一个问题,即后者能够进一步改善前者的预测精度吗?图8给出了这一问题在实证中的不甚清楚的答案。从图中可以看出,基于递归方法和基于滚动方法,对这一问题的回答并是不一致的,前者倾向于肯定三变量模型,后者倾向于否定三变量模型。但可以看到,即便递归方法给出了某些情况下可以进一步改善的结果,改善的幅度也不高,尤其是2或者2个季度以上的预测,改善的幅度至多2%左右。
5 结论
本文没有采用复杂模型,而是选取最为简单和基本的AR以及VAR模型,来分析和比较它们在预测中国通货膨胀的表现,以求弥补中国通胀预测方面研究的不足,并且得到了以下几点结论:(1)通常,滞后阶数较少的模型对通胀的预测准确度较高;(2)预测期越长,考虑一定“结构”信息的模型的预测表现越优于简单的随机游走式预测;(3)若只要引入一个变量作为额外信息,并且基于VAR模型进行预测,绝大多数情况下,M1增速、名义GDP增速和真实GDP增速都能改善仅仅依赖历史通胀信息形成的预测,但M0增速、M2增速以及PPI通胀,均不能提高单变量的AR(1)模型的预测精度;(4)若引入两个变量作为额外信息,并且基于VAR模型对通货膨胀进行预测,绝大部分模型都能优于单变量的AR(1)模型,但相对含有M1增速的两变量VAR(1)模型则没有明显的改进。
良好的中国通货膨胀的预测,不仅可以为中国的货币政策制定提供“前瞻”依据,而且可以成为某些理论研究的实证材料。目前,中国通货膨胀预测方面的研究程度与该问题本身的重要性很不相称。本文虽然分析了时间序列模型当中最为重要和基本的两类模型:AR和VAR模型,并得到了一定的结论。但仍有许多方面值得进一步的深入研究,比如,如何对季节性部分进行预测,考虑到通胀某种形式的非线性行为,考虑到通胀的条件异方差能否提高预测精度等等。另外,本文的模型比较仅仅利用了RMSE,没有考虑其他的基于统计量的模型预测比较方法。这些都是值得进一步研究的问题。
[1]陈彦斌,唐诗磊,李杜.货币供应量能预测中国通货膨胀吗[J].经济理论与经济管理,2009,(2).
[2]王少平,彭方平.运用SETAR模型对我国通货膨胀的拟合与预测[J].统计与决策,2006,(7).
[3]Andrew Ang,Geert Bekaert,Min Wei.Do Macro Variables.Asset Mar⁃kets or Surveys Forecast Inflation Better?[J].Journal of Monetary Eco⁃nomics,2007,(54).
[4]Atkeson,A.,L.E.Ohanian.Are Phillips Curves Useful for Forecast⁃ing Inflation?[J].Federal Reserve Bank of Minneapolis Quarterly Re⁃view,2001,(25).
[5]Gosselin,Marc-André,Greg Tkacz.Evaluating Factor Models:An Ap⁃plication to Forecasting Inflation in Canada[Z].2001.
[6]Hamilton,J.Time Series Analysis[M].New Jersey:Princeton University Press,1994.
[7]Lütkepohl,Helmut.New Introduction to Multiple Time Series Analysis[M].Berlin:Springer,2006.
[8]Marcellino,M.,James H.Stock Mark W.Watson.Macroeconomic Forecasting in the Euro Area:Country Specific Versus Area-wide In⁃formation[J].European Economic Review,2003,(47).
[9]Moser,Gabriel,Fabio Rumler,Johann Scharler.Forecasting Austrian Inflation[J].Economic Modelling,2007,(24)

