灵活选取参考系
孙冬子 贾安娜
(陕西省永寿县中学,陕西 永寿 713400)
描述物体运动状态的物理量如位移、速度、加速度等都具有一定的相对性,其原因是上述各物理量必须相对于某一参考系才具有实际意义.对同一物体而言若选择不同物体为参考系上述各物理量可以不同,在解决直线运动类问题时大多数同学习惯选择地面或相对地面静止的物体为参考系,但对相对运动类问题这样做可能不利于解题,我们不妨选择其中相对运动的物体为参考系.
如图1所示,在水平地面上甲乙两物体分别以初速度v1、v2,加速度a1、a2作匀变速直线运动,在运动过程中任意时刻他们的瞬时速度大小分别为v甲、v乙,则有
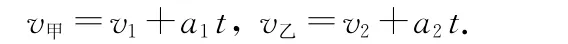

图1
如果我们选择甲物体为参考系可得任意时刻乙物体相对甲物体的速度为

上式类比匀变速直线运动基本公式vt=v0+at可得,若以甲物体为参照系,则乙物体的初速度v0相、加速度a相分别为

由此我们可以得到一个很重要的结论:若以运动的物体为参考系时,必须把其自身所具有的速度以及加速度反向叠加到研究对象上去.在此结论基础上我们很容易推导出任意时刻乙物体相对于甲物体发生的位移s.
设甲、乙在时间t内的经过的路程分别为s甲、s乙,则有
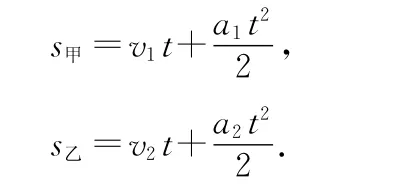
可得
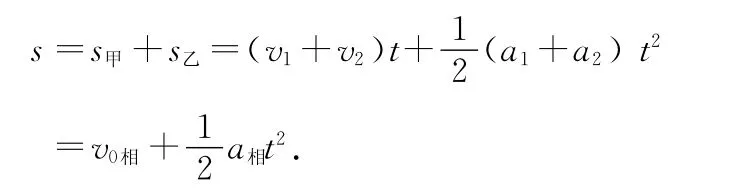
由上可见,此种思想方法解决物体的相对运动类问题比较方便.
例1.如图2所示,一平板车以初速度v0向右匀速行驶,某时刻将一货箱(可视为质点)无初速度的放置于平板车上,货箱离车后的距离L=3m,在货箱放在车上的同时,平板车开始刹车,平板车在刹车的过程中可视为做加速度a=4m/s2的匀减速直线运动,已知货箱与平板车间的动摩擦因数μ=0.2,取g=10m/s2,为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
解法1:货箱无初速度放在平板车上,由于惯性会相对于平板车向后滑动,在此过程中货箱则在摩擦力的作用下向右作初速度为零的匀加速直线运动,而平板车作匀减速直线运动,当两者速度相等时若货箱没从平板车上掉下来,则此后货箱将相对于平板车向右滑动,所以当货箱速度与平板车速度相等时还未从平板车上掉下则以后将不会从车上掉下来.

图2
设经时间t后两者速度相等,以货箱为研究对象,由牛顿第二定律得货箱向右的加速度a′=μg,则货箱向右发生的位移
以平板车为研究对象其向右发生的位移为s=v0t-又a′t=v0-at,为使货箱不从平板车上掉下来则应满足s-s′≤L,联立以上几式解得

代入数值得v0≤6m/s.
解法2:以平板车为参考系,应将平板车所具有的速度以及加速度反向叠加到货箱上,因此以平板车为考系后货箱具有向左的初速v0,向右的加速度a相=a+μg,因此货箱相对于平板车向左做初速为v0的匀减速直线运动,要使货箱不从平板车上掉下来,应满足货箱速度减为零时相对于平板车发生的位移小于等于L,则由

其中s≤L得

代入数值得v0≤6m/s.
例2.A、B两辆汽车在笔直的公路上同向行驶.当B车在A车前L=84m处时,B车速度为4m/s,且正以a=2m/s2的加速度匀加速运动;经过一段时间后,B车加速度突然变为零,A车一直以20m/s的速度匀速运动.经过12s后两车相遇.问B车加速行驶的时间是多少?
解法1:设A车的速度为va.B车加速行驶时间为t,两车在t0时相遇,相遇时两车行驶的路程分别为sa、sb,则有

依题意有
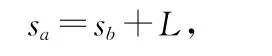
由以上3式得

代入数据有

解得 t=6s或18s.
t=18s不合题意,舍去.因此,B车加速行驶的时间为6s.
解法2:以B车为参考系,将B车所具有的速度以及加速度反向叠加到A车后,A车经历两个运动过程,先经过匀减速运动再经过匀速运动直到相遇,设B车加速行驶的时间为t,A车相对于B车作匀减速运动与匀速运动时行驶的路程分别为sa、sb,则有

依题意有

由以上几式解得t=6s或18s.
t=18s不合题意,舍去.因此,B车加速行驶的时间为6s.
由以上两例可见,解决相对运动类问题参考系的选取非常重要,参考系选取恰当可以使问题在很大程度上得到简化,相反,若参考系选取不当可能使问题变得更加繁琐,甚至解不出正确答案.
——兼谈参考系与坐标系的关联关系

