让学生通过实例推演来领会卫星变轨问题

毛小平

（贵州省盘县二中，贵州 盘县 553500）

卫星变轨问题是中学物理教学的一个难点，其原因在于学生对变轨问题的理论推演较难理解.如果我们将卫星变轨问题的理论推演改为实例推演，那么学生在老师的引导下通过自己的推演就能很快的掌握卫星变轨的有关问题.

图1

由开普勒第二定律知

设卫星在半径为2R的圆形轨道上做匀速圆周运动的速度为V3，则

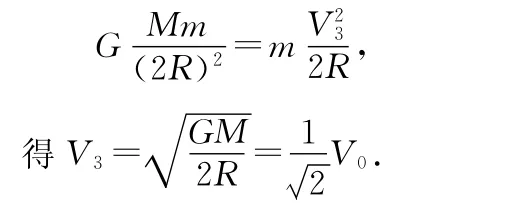
通过以上计算可知，欲使卫星从椭圆形轨道2进入圆形轨道3需让卫星在运行到椭圆形轨道的远地点B时点火加速，使其速度由增大到

学生在教师的引导下完成了以上卫星变轨问题的实例推演后，自然就会对卫星变轨的相关问题搞清楚了.

实例推演的关键在于给定合理的数据，也就是欲从半径为r1圆形轨道进入长轴为（r1＋r2）椭圆形轨道时，其速度需要从增大到多少.

卫星从近地点A运动到远地点B的过程中机械能守恒.

由开普勒第二定律知

由（1）～（3）式就可求出我们需要的VA.

如将r1＝R，r2＝2R代入，即可求得（其中V0为第一宇宙速度）.即欲使卫星从近地圆轨道进入近地点距地心为R、远地点距地心为2R的椭圆形轨道，需要卫星在近地点点火加速，使其速度由V0增大到这就是我们给学生的合理的数据.我们还可以用上面的计算方法给出其它的合理数据以供学生推演卫星变轨之用.如欲使卫星从半径等于地球半径两倍的的圆形轨道进入近地点距地心为2R，远地点距地心为3R的椭圆形轨道，需要卫星在近地点点火加速，使其速度由增大到有了这些合理的数据，学生就可以推演卫星变轨的过程了，通过自己的推演去理解“卫星从低轨道到高轨道历经两次加速后，其速度为什么不但不增反而减小”等变轨问题，这对中学物理突破卫星变轨的教学难点是很有帮助的.