基于不同安全间距的元胞自动机交通流模型的研究

梁文家， 关 可 ， 吴潜蛟， 盛 春

（1.长安大学 电子与控制工程学院，陕西 西安 710064；2.长安大学 信息工程学院，陕西 西安 710064）

随着社会经济的发展，交通问题越来越成为被关注和研究的焦点，对交通流的模拟和交通流特性的理解是解决交通问题的前提和基础。传统的交通流模型有流体力学模型、气体动力学模型、跟驰模型等[1-2]，这些模型在理论研究和实际应用中都已经发挥了重要作用。然而由于交通流在时间、空间上具有高度的随机性、动态性和复杂性，交通系统表现出丰富的非线性特征。另一方面，真实交通系统的一般路网规模巨大，道路使用者众多，传统的微观仿真方法面临着计算资源的约束，因此要求有结构简单、计算迅速的交通流模型。

目前基于元胞自动机（Cellular Automata，CA）的交通流模型研究取得了很大进展。Cremer和Ludwig[3]于1986年最早将元胞自动机理论应用于车辆交通系统的研究，为研究交通流系统开辟了新的途径；Wolfram[4-5]同时期提出了184号CA模型用于交通流的模拟。以Wolfram命名的184号CA模型为基础，Nagel和Schreckenberg于1992年提出了用于研究高速公路交通的NaSch模型[6]，同一年，Biham等人提出了用于研究城市网络交通的BML模型[7]。

因为涉及到车辆、司机、行人、道路条件等因素以及它们之间的相互作用的影响，交通系统通常被看作是一个由多粒子构成的复杂的巨大系统。CA模型在保留了交通流系统的非线性特征和其他物理特征的同时，CA模型的时间、空间、状态变量均为离散量，元胞的状态并行更新，适合在计算机上实现，能够实现大规模路网的快速计算。由于大量车辆组成的交通流从本质上说是离散量，而元胞自动机又是一个完全离散化的模型，所以用元胞自动机原理来研究交通流的问题就具有独特的优越性，可以用元胞自动机来研究各种具体的交通现象。由于CA模型的这些特性，其非常适合用于交通流的仿真模拟，而且，如果演化规则设计合理，并考虑到真实的交通条件，交通流的很多特性可以通过仿真模拟出来，从而可以解释很多的交通现象。

元胞自动机模型在交通流仿真中的各种优点，已经引起很多学者的重视和研究。研究方向有：改进CA模型相关的规则，考虑各种真实的交通条件，对仿真结果的时空图和基本图进行分析；CA模型中随机参数的标定的研究；基于CA模型的交通流的在线模拟等。

1 NaSch模型

作为184号模型的推广，1992年Nagel和Schreckenberg提出了著名的用于描述高速公路交通流的NaSch模型[6]。在模型中，时间、空间以及速度都被整数离散化，道路被划分为离散的格子（即元胞），每个元胞或者是空的，或者被一辆车占据，每辆车的速度可以取 0，1，2，…，vmax，其中vmax为最大车速。所有车辆由左至右编号，其中第n辆车的位置记为xn，而它的速度vn∈{0，1，2，…，vmax}，其中n∈1，2，…，N，且假定所有车辆具有相同的最大速度vmax（≥1）。车辆n+1在车辆n前方，两车间距dn=xn+1-xn-1表示第n辆车和其前面的近邻车辆第n+1辆车之间的空元胞数。单元格长7.5 m，时间步长1 s。

在t→t+1的过程中，Nasch模型按照如下的规则同步并行更新：

1） 加速过程，vn→min（vn+1，vmax）；司机希望以最大的车速行驶。

2） 减速过程，vn→min（vn，dn）；司机为了避免和前面的车发生碰撞而采取的减速措施。

3） 随机慢化，以概率p，vn→max（vn-1，0）；因为各种不确定因素（如前面路况不好、司机的不同心态等等）造成的车辆随机减速。

4）车辆向前运动，xn→xn+vn；车辆按照调整后的速度向前行驶。

这4步是能够反映真实交通现象的最小化规则集，缺少任何一条规则或者改变执行的顺序都不能产生真实的交通行为。

NaSch模型虽然具有十分简单的形式，但是却可以描述一些实际的交通现象，比如NaSch模型能够再现阻塞的自发形成和自发消失，拥挤交通情况下时走时停的现象等等。NaSch模型的基本图如图1所示，包括自由流和拥挤流两个分支。该模型考虑到了车辆的加速、减速和随机慢化的影响，在时空图上能显示出车辆从自由运动相到局部阻塞相的相变，从而引起了广泛的注意和研究。

图1 NS模型的基本图Fig.1 Basic diagrams of NS model

在上面的基本图中，vmax=4，即对应实际的车速为108 km/h，系统有300个元胞，即车道由300个离散格点，记录在[101～300]时间范围内的200个时间步长。图中流量达到最大值时对应的密度值称为临界密度，记为ρc。注意到当p=0时，临界密度 ρc=1/（Vmax+1），这与确定性 NS 模型（p=0）是一致的。 当p>0时，临界密度ρc要比p=0时的临界密度要小。

对于不同的减速概率来说，当密度小于ρc时，车辆的行驶为自由流状态，相互之间不受影响，以最大速度行驶。当密度大于ρc时，系统出现自发的局部堵塞，且堵塞随时间的推移向上游传播，堵塞流和自由流在系统中共存。但值得注意的是，慢化概率p对NaSch模型的模拟结果有很大的影响，慢化概率p是引起车辆自发堵塞的原因。

董力耘等人[8]提出一种改进的CA跟车模型，除考虑前后车的相对速度外，通过引入定值的安全间距dsafe来描述车辆的减速行为。

Li X B等人[9]提出了一个能近似考虑前车速度效应的CA扩展模型，建模时考虑了前车速度可能的影响，对减速条件进行了改进，然后再计算本车的车速，并且保持了更新规则的同步并行性。

在VDR模型中，随机慢化概率不再是固定不变的，而是车辆速度的函数，采用下式来计算随机慢化概率：

并且取p0>p，这是考虑到在上一时刻静止的车辆在新时刻的随机慢化概率要大于上一时刻运动的车辆。确定随机慢化概率要放在加速步的前面来运行，也就是说，随机慢化步的慢化概率是由上一时刻更新结束后的车辆的速度决定的。

在VDR模型中，随机慢化步的规则为：如果vn=0，那么以概率p0，vn→max（vn-1，0）；如果vn>0，那么以概率p，vn→max（vn-1，0）。

2 改进的元胞自动机交通流模型

考虑车辆间距的跟驰行为，在一队汽车中，后车驾驶员总不愿意落后很多，而是紧随前车前进，这就是“紧随要求”。从安全角度考虑，跟驰车辆要满足2个条件：1）后车的车速不能长时间地大于前车车速，只能在前车速度附近摆动，否则会发生碰撞，这是“车速条件”；2）前后车之间必须保持一个安全距离，即在前车刹车时，有足够的时间供后车驾驶员做出反应，采取制动措施，这是“间距条件”。显然，当车速高时，制动距离大，跟车距离也应加大。紧随要求、车速条件和间距条件构成了车队跟驰行驶的制约性，即前车车速制约着后车车速和两车间距。驾驶员对前车运行状态的改变要有一个反应过程，这个过程需要一定的时间，即反应时间。一般来讲，人脑对一个输入的信息作出判断大约需要1 s左右。

文中在NaSch模型的基础上提出一个改进的元胞自动机模型来模拟周期性边界条件下高速公路上的车流运动。考虑到车辆速度的差异，对速度不同的车辆设置不同的安全车间距，根据车辆与前方紧邻车辆之间的间距和车辆的速度来确定该车的运动，这样就可以间接地反映出前方紧邻车辆对当前车辆的影响。通过引入不同的安全间距可以描述以不同速度运动的车辆接近前方车辆时的减速行为。文中采用了不同的安全车间距，并且考虑到速度的差异，因而改进后的交通流模型可以较好地描述交通流中的现象，对车辆微观运动进行合理地描述。

文中的改进模型定义由L个格点组成的一维离散点列上，每个格点上可能有vmax+2个状态：空格点（即无车），或者有一辆以速度v运动的车，其中vn∈{0，1，2，…，vmax}，n∈1，2，…，N，且假定所有车辆具有相同的最大速度vmax（≥1），车辆n+1在车辆n前方。

改进后的交通流模型考虑到车辆当前速度的差异，对速度不同的车辆设置不同的安全车间距。车辆的演化规则为：

确定随机慢化概率：考虑到慢启动规则，慢化概率不再是固定不变的，而是车辆速度的函数，采用下式来计算随机慢化概率：

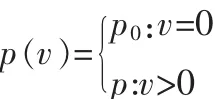
1） 加速步：vn→min（vn+1，vmax）；司机希望以最大的车速行驶。

2） 减速步改为：whilevn=0，1，2；vn→min（vn，dn）；

whilevn=3，4；vn→min （vn，dn-1）；（如果dn=0，那么vn→min（vn，dn））；

whilevn=5，6；vn→min （vn，dn-2）；（如果dn=1，0，那么vn→min（vn，dn））。

dn=xn+1-xn-1表示第n辆车和其前面的近邻车辆第n+1辆车之间的空元胞数，xn+1表示第n+1辆车的位置，xn表示第n辆车的位置。

3）随机慢化步：其规则是如果vn=0，那么以概率p0，vn→max（vn-1，0）；如果vn>0，那么以概率p，vn→max（vn-1，0）。

4）车辆运动步：xn→xn+vn；车辆按照调整后的速度向前行驶。

从上面的车辆运动的演化规则可以看出，该模型与NaSch模型不同之处在于：

考虑到车辆速度的差异，对速度不同的车辆设置不同的安全车间距，根据车辆与前方紧邻车辆之间的间距和车辆的速度来确定该车的运动，这样就可以间接地反映出前方紧邻车辆对当前车辆的影响。另外，通过引入不同的安全间距可以描述以不同速度运动的车辆接近前方车辆时的减速行为。当车速高时，制动距离大，跟车距离也应加大，这也符合实际情况和日常经验。

同时，在改进的模型中的随机慢化步采用了VDR模型，对不同速度的车辆采用不同的慢化概率，在上一时刻静止的车辆在新时刻的随机慢化概率要大于上一时刻运动的车辆。

3 仿 真

为了对改进后的模型有一个直观的认识，笔者用改进的模型并利用Matlab工具对单车道交通流进行仿真。模拟过程中，系统长度L=300个元胞，记录在[501～1 000]时间范围内的500个时间步长，采用周期边界条件。由于系统是封闭的，则平均密度ρ=N/L，N是道路上的车辆数目。初始状态时N辆车随机分布在L个一维离散的元胞表示的路段上，其速度从0到vmax随机选取一个整数值，从左到右车辆依次从1到N标记。在每个更新时步，N辆车的速度按照更新规则并行刷新。为了模拟比较方便，选取更新时间步为1 s。一个元胞长+500 s之后开始记录数据，以消除初始状态暂态过程的影响。

图2，图3，图4为交通流时空演化图，水平方向自左向右为车辆的运动方向，垂直方向自上而下为时间演化方向。仿真的结果表明，在低密度区是自由交通流，在高密度区，出现交通拥挤。图2为低密度时自由流的时空图，流量随密度的增加而增加。图3，图4表示高密度时的时走时停的交通流时空图，颜色较浅的区域对应于没有拥挤的自由流，颜色较深的区域表示出现拥挤。

图2 改进模型的自由交通流时时空演化图vmax=6，p=0.3，p0=0.6，ρ=0.05Fig.2 Free traffic flow space-time evolution of the improved model

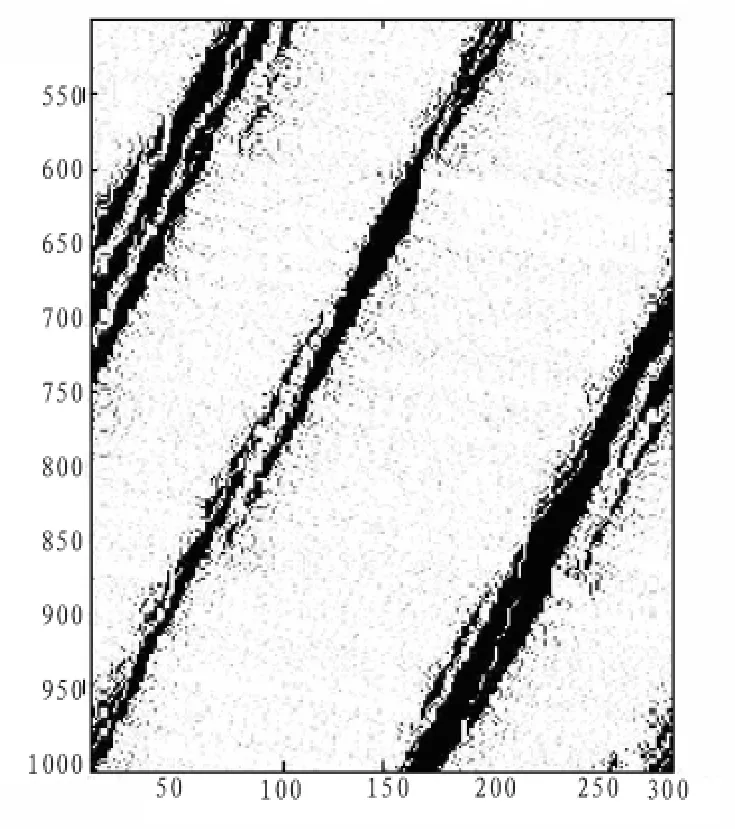
图3 改进模型的时走时停交通流的时空演化图vmax=6，p=0.1，p0=0.6，ρ=0.2Fig.3 Stop-go traffic flow space-time evolution of the improved model

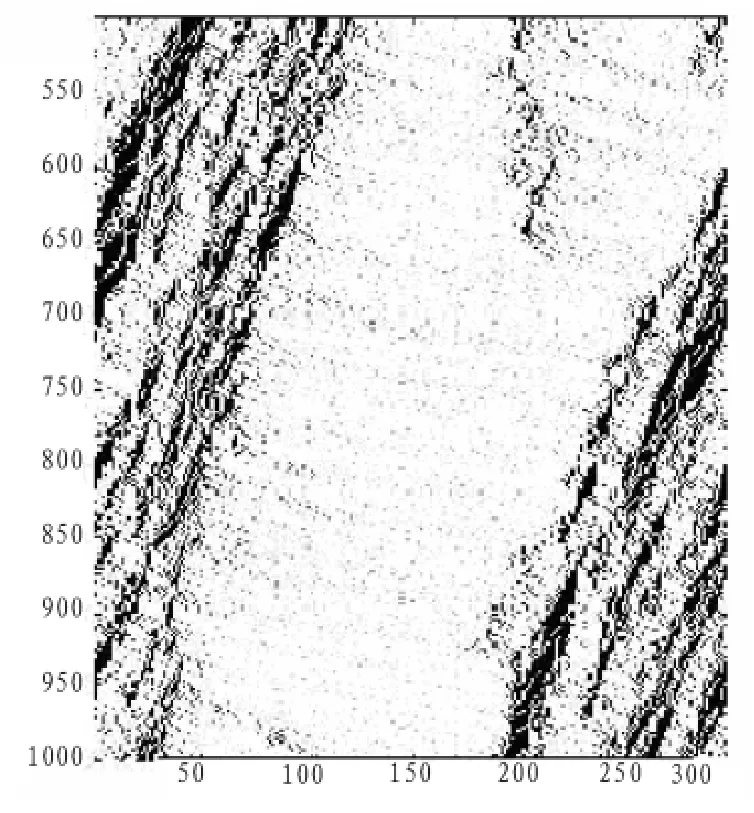
图4 改进模型的时走时停交通流的时空演化图：vmax=6，p=0.5，p0=0.6，ρ=0.2Fig.4 Stop-go traffic flow space-time evolution of the improved model

从图3，图4中可以观察到自由流和堵塞流交替出现，堵塞向后传播。车辆由最初车速较高的自由流，随着车头间距减小、车速降低，逐渐形成堵塞。如果速度进一步降低，堵塞的范围将增大。在堵塞流的内部，车辆会与前车保持一定间距行驶，或者处于静止状态。在堵塞流外面的颜色较浅的自由流区域，车辆间距比较大，车辆会以较高的速度自由行驶，而不会发生碰撞，直到间距变小，形成另外一个堵塞流。从图3，图4还可以观察到减速概率p对模拟结果的影响，在其它参数不变的情况下，由于减速概率p的增大，局部更容易形成堵塞。

改进模型中驾驶员反应的敏感性增强，相接近的车辆间会根据不同速度来保持不同的间距，避免急刹车情况，从而保障交通安全。

这一结果对交通的控制和管理具有一定的参考价值。

图5为改进模型和NS模型的基本图的对比。评价一个交通流模型的最重要的指标就是基本图。仿真结果表明，在低密度区流量随密度的增大而增大，流量达到最大值之后，随着密度的进一步增大，流量持续减小。

图5 改进模型和NS模型的基本图Fig.5 Basic diagrams of improved model and NS model

从图5中还可以观察到，改进模型中的基本图曲线在大于临界密度之后的下降趋势比NaSch模型的基本图曲线要大。这也说明改进模型中驾驶员的反应敏感性增强，驾驶员的加、减速反应都比NaSch模型中的要快，所以流量的变化就越明显。

4 结束语

文中对NaSch模型进行了改进，建立了一个扩展的元胞自动机模型来模拟单车道交通流。该模型通过设置不同的安全间距，根据车辆与前方紧邻车辆之间的间距和车辆的速度来确定该车的运动，这样就可以间接地反映出前方紧邻车辆对当前车辆的影响。

通过对改进模型的仿真后，可以看到驾驶员的反应敏感性增强，能迅速地做出决策，保证了交通的安全。数值仿真结果显示：流量随密度的变化显著，基本图曲线下降的趋势更明显了。

由于改进模型只是修改了NaSch模型的局部规则，并不影响原来模型的计算的并行性，所以保持了NaSch模型原有的计算速度快等诸多优点，对智能交通的设计具有一定的参考价值。

[1]Kerner B S.Three phase traffic theory and highway capacity[J].Physica A，2004（333）：379-440.

[2]Schadschneider A.Traffic flow：a statistical physics point of view[J].Physica A，2002（313）：153-187.

[3]Cremer M，Ludwig J.A fast simulation model for traffic flow on the basis of Boolean operations[J].Mathematics and Computers in Simulation，1986（28）：297-303.

[4]Wolfram S.Theory and applications of cellular automata[M].Singapore：World Scientific，1986.

[5]Wolfram S.Statistical mechanics of cellular automata[J].Rev.Mod.Phys，1983（55）：601-644.

[6]Nagel K，Schreckenberg M.A cellular automaton model for freeway traffic[J].Journal of Physics I France，1992（2）：2221-2229.

[7]Biham O，Middleton A A，Levine D A.Self-organization and a dynamical transition in traffic flow models[J].Physical Review A，1992（46）：6124-6127.

[8]董力耘，薛郁，戴世强.基于跟车思想的一维元胞自动机交通流模型[J].应用数学和力学，2002，23（4）：331-337.

DONG Li-yun，XUE Yu，DAI Shi-qiang.One-dimension cellular automaton model of traffic flow based on car-following idea[J].AppliedMathematicsandMechanics，2002，23（4）：331-337.

[9]LI X B，WU Q S，JIANG R.Cellular automaton model considering the velocity effect of a car on the successive car[J].Physics Review E，2001（64）：66-128.