二维图形封闭区域自动识别算法
艾迪,周云燕,万里兮
(中国科学院微电子研究所 北京 100029)
微电子领域,常用的商用仿真软件如Cadence,HFSS,对于实体、层、网格等等单元的操作都会大量使用到多边形处理的各种算法。比如鼠标点击选中相应单元的操作需要用到点是否在多边形内的算法;绘制版图时需要大量用到多边形的合并,分割、删除等算法。这些软件只能对已经存在的多边形进行这些操作。然而有些时候从DXF文件导入的版图中仅含有线段信息,不含多边形信息;或者需要对椭圆、圆弧等其他实体围成的封闭区域进行这种类似多边形操作。对于这些情况这些软件就无能为力。本文在实际电磁仿真软件开发的基础上提出的图形封闭区域识别算法很好的解决了这个问题。
这种识别算法输入可以是任意的线段、圆弧信息,输出则为所有的封闭区域(包含多边形)。在处理过程中首先需要对于已知线段集合求出所有交点信息。而这种求交点已经有了快速高效的算法。本文应用了这种高效的算法,并增加了它的适应性以支持圆弧。在封闭区域的搜索过程中,本文采用了一种类似于计算机图形学中广泛应用的图的广度优先遍历搜索算法。该算法原本目的是路径搜索发现,本文在算法实现过程中加以修改,拓展了图的相邻表储存结构,使之能够发现图中封闭的区域,同时又保持了算法本身低时间复杂度的特性。
1 基本理论
在二维的计算几何学问题中,每个输入单元都用一个点的集合{pn}来表示,其中每个 pi=(xi,yi),xi∈R,yi∈R。 输入单元可以是简单的点、线段、圆弧或是多边形,在本文的算法中还有可能是一段折线。用点集表示多边形P时,可以按照在P的边界上出现的逆时针或是顺时针顺序排列的顶点序列来(p1,p2,…,pn)表示。
对于圆弧,一般计算机中需要用3组信息来储存,分别是圆弧的起点、终点以及弧度值大小。圆弧可能是圆的一部分,也有可能是一段任意的曲线。在本文的算法中,对圆弧的处理只会用到圆弧与其他单元的交点,以及圆弧上点的次序。因此在计算完交点后,圆弧可以当作一般线段处理,即可用圆弧上顺序排列的点(p1,p2,…,pn)来表示。
本算法与一些其他图像识别算法(如文献[1])不同之处在于输入为点集{pn}表示的线条信息,输出结果为一系列顶点(p1,p2,…,pn)表示的封闭区域。 这种结果的表示形式可以用来做很多后续计算。因此本算法可以成为很多其他图形算法的接口。例如:多边形的剪裁[2-3],判断点与多边形的位置关系[4]等。
文中讨论的多边形都属于简单多边形。简单多边形具有下列性质:1)所有顶点各不相同, 即:坌i≠j⇒v≠v;2)任何顶点都只属于它所在的边;3)任意两条边都不相交。本文算法输出的封闭区域结果也符合上述性质。
1.1 求交点
在输入任意线段、圆弧等信息后,本文算法第一步为求出它们之间所有的交点。方法如下:
第一步:先求出所有线段的交点。输入的线段可能存在很多特殊情况,如两条线段有一部分重合,或是互相垂直。文献[5]中的Bentley-Ottmann(1979)算法能够很好应对这些情况。如果N条线有K个交点,该算法能在O(N+K)log N的时间复杂度下计算完所有的交点,而不会有遗漏。文献[6]给出了求单个交点的方法,它与上述算法结合使用。
第二步:增加圆弧的处理。由于圆弧的特殊性,一段圆弧与一条线段可能有多个交点,并且第一步算法中采用的扫描线判断线段顺序的方法对于圆弧不再有效,因此需要单独计算出每个圆弧与其他部分交点。
所有交点都计算出后,可以根据这些信息构建出一个图G=(V,E),如图 1(a),V 为交点,图中用圈表示,E 为其中 2个交点相连的边界。对于圆弧则可以忽略其弧度信息,当作普通的线段边界E进行处理。

图1 无向图和对应的扩展邻接表结构Fig.1 An undirected graph and its extended adjacency-list representation
1.2 扩展的邻接表表示法
在本文算法中采用了图G=(V,E)的邻接表[7]表示方法。这种方法的好处是表示稀疏图(图形的边界数E远小于顶点数V的平方)比较简洁紧凑。一般版图结构中多边形结构占了主要部分,因此属于稀疏图的范畴。另一种好处是本算法需要从一个源点进行广度遍历向外扩展搜寻,而发现的封闭区域信息则就地储存在节点中。邻接表节点的链表结构,在本例中稍加修改和扩展就能满足一些封闭区域识别的需求,如存储封闭区域的路径信息。
在本文算法中,将邻接表结构扩展如图1(b)所示。将每个节点增加了4种数据结构。它们分别作用为:COLOR代表节点的颜色,这样是为了保持搜索的轨迹;P代表这个节点的父节点;D代表本节点到源节点的距离;M是个链表结构,它记录着已发现的封闭区域相关信息。4种数据缺一不可。
1.3 基于广度优先算法的封闭区域发现算法
广度优先算法又可以叫宽度优先算法,在计算机图形学中广为应用,是最简便和直观的图的搜索算法之一,在文献[7]中有详细介绍。它的直接目的是遍历搜索图和寻找最短路径。本文算法采用了和广度优先搜索算法类似的思想用于搜索图中封闭区域。原理如下:
已知图G=(V,E)和一个源顶点s,广度优先算法以一种系统的方式搜索G的边,从而遍历s能达到的所有顶点。这种算法一直通过一条已找到和未找到顶点之间的边界扩展。具体做法为将位于这条边界的点着上灰色,表明下一步要从这些点向外搜索;将已经经过的点着上黑色作为标识,使搜索不致走回头路。其它未探索的点为白色。图2(a)所示为算法初始阶段。经过一轮搜索,灰色边界点附近的白色点都被发现并标上灰色,而之前的灰色点由于完成了对附近点的搜索就被标上了黑色,如图2(b)。算法继续重复这个过程以发现更多的外围点,如图 2(c)。

图2 广度优先搜索算法Fig.2 Breadth-first-search procedure
这样如此反复,最终所有可到达的白色点都被发现。因此这种广度搜索算法的由内向外遍历所有点的性质满足了本文算法需要搜索出图中所有封闭区域的基本要求。
更进一步观察,这种广度搜索算法就如向纵横交错的沟渠中倒一桶水,水沿着沟渠的路径向四面八方扩展开去,最终到达所有位置。如果图中有封闭区域,就像沟渠中一个环路,在水流向四周蔓延时肯定会有两股水流于某一时刻在环路另一端相遇。如在图2(b)的封闭区域1旁,探索分支s→m与 s→n 在 E(m,n)这条边“相遇”;在图 2(c)的封闭区域 2旁,探索分支m→r与n→r在同一个r点“相遇”。
由于图中有封闭环路时两个探索分支会“相遇”,并且走在最前的点一定是灰色点,因此在广度优先算法遍历过程中,如果两个灰色点“相遇”,那么就可以判断发现了一个封闭区域。
2 封闭区域分离算法
本文封闭区域分离算法的关键就在如何对图进行广度优先遍历时两个灰色点相遇的情况进行判断和记录。在最后,算法还需要通过这个相遇信息完整提取出所有封闭区域信息,并以在这些区域边界上按顺序排列的顶点集{Pn}的形式表示出。
2.1 记录相遇点
在对图进行广度优先搜索时,灰色点相遇会存在2种情况。这2种情况可以分别用图3的(a)、(b)来表示。

图3 灰色点相遇的两种情况Fig.3 Two cases of grey points encounter
直观上来看,第一种情况是灰色边界中有两个或两个以上灰色点“相邻”,如图 3(a)中的 n、x、y这 3个点。 有 2 个边分别连接n、x与x、y;另一种是两个或两个以上灰色点会通向同一个白色未探索点,如图3(b)中的r、n、x这 3个点。这3个点没有直接连接,但是下一步它们会同时向y点去探索。
可以看出由于组成封闭区域顶点的个数可能是偶数,也可能是奇数,才会导致这两种情况。由于算法每次只是从一个灰色点开始依次向外探索扩展,所以无论哪种情况,当相遇发生时,总是会有个灰色点a发现它要探索的下一个点b已经被另一个灰色点所占据。这时只用在点b对应的相遇链表数据结构M中增加点a这一项,表示从点a过来的搜索分支也到达了b处。这个链表M存放在本文1.2所述的邻接表扩展结构中。
例如对于图3(a)所述的相遇第一种情况,搜索记录过程如下:
假设在n、x、y这3个灰色点中从n最先开始向外探索。n发现它的临界点x已经成了灰色,那么在x对应的相遇链表结构M[x]中增加一条对于n记录,用于构建封闭区域Ⅰ。n探索完毕,自己由灰色变成了黑色,如图4(a)。接着节点x开始向外探索,它对于已经变黑的n节点不作理会,而发现了灰色的y节点。因此在y的链表M[y]中增加一条记录x用于构建封闭区域Ⅱ。x探索完毕变成黑色,如图4(b)。图中的虚线代表了相遇情况。至此两个封闭区域都Ⅰ、Ⅱ被探索出来,分别在 M[x]和 M[y]中有所记录,如图 4(c)。
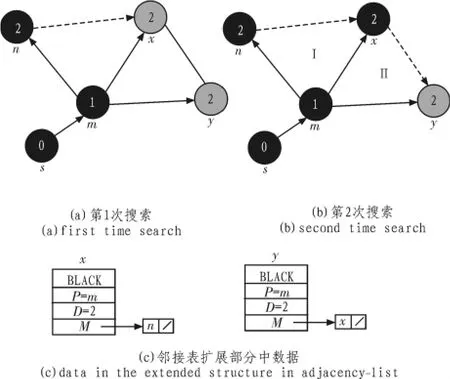
图4 对于图3(a)的搜索记录过程Fig.4 Search and record process for fig.3 (a)
对于图3(b)的第2种情况,搜索过程如下:

图5 对于图3(b)的搜索记录过程Fig.5 Search and record process for fig.3 (b)
假设在r、n、x这3个点中从n最先向外搜索。n发现了白色节点y。作为广度搜索的正常步骤,y节点变成灰色以表示被搜索发现。n搜索完成,如图5(a)。接着r、x在各自的搜索过程中都发现了灰色点y,如图5(b)。它们分别在y的链表 M[y]中添加了 r、x这两条记录,如图 5(c)。 这两条记录分别对应着左、右两个四边形区域Ⅰ、Ⅱ。
通过对这两种情况的分析,可以发现在记录两个灰色点相遇的过程中,一个灰色点在完成搜索记录后就变成了黑色。这样另一个点就不会对同一个封闭区域进行重复记录。同时,由于对相遇点的记录M采用链表结构,能够记录同一点上的多次相遇,这样就能反映出多个封闭区域共用一个顶点的情况。
2.2 需要记录的额外信息
为了在读取记录时能够知道是在上述哪种情况下 “相遇”,需要在广度搜索时记录下每个顶点到源点的距离值D。在图3~5中,节点中的数字代表这个距离值D。源节点s的D值为0。当节点a探索到一个新节点b,b的D值会在a的D值上加1。 如图 5(b)中从n搜索到y,则D[y]=D[n]+1=3。
如果只知道在哪一点相遇,还不足以形成由顶点序列(p0,p1,…pn)来表示的完整的封闭区域信息。因此假设从顶点u开始向外搜索时,每发现一个白色顶点v,就需要将u作为v的父节点存在v的邻接表结构P中。在图3~5中,实心箭头表明了节点之间的“父子”关系。例如5(b)中,m为n的父节点,故P[n]=m;n为y的父节点,故P[y]=n。因为一个节点最多只能被发现一次,所以任何节点最多只有一个父节点。通过这种记录,在搜索完成后,对任意一个节点,都能重现一条返回源节点的路径。如对于图5(b)中的y,就有y→n→m→s。
上述两个额外信息:距离与父节点,都储存在邻接表扩展结构中,如图 4(c)、图 5(c)。 它们都用于搜索完成后重构封闭区域信息。
2.3 输出封闭区域信息
当搜索完成后,选出一个含有相遇链表信息M的节点u。u自身有一条不断通过u的父节点直到源节点构成的主路径{u→P[u]→P[P[u]]→…→s}。而M[u]指向的每一个节点也都各自有一条主路径。u的主路径和任意一条M[u]指向节点的主路径都围成了一个封闭区域,因此这两条路径会有一个相同的起始点。找到这个起始点,即可知道围成的封闭区域的所有顶点信息。
找到这个起始点的方法为,首先判断构成封闭区域的顶点数为奇数还是偶数。例如对于图4(b),点y的M表中含有x点,比较距离值D[x]与D[y],它们相等表明区域Ⅱ由奇数个点组成。因此直接从y和x的主路径y→m→s与x→m→s同时往回寻找,直到找到了相同的起始点m,即可出构建区域Ⅱ(x,y,m)。实现方法为比较 P[y]、P[x],再比较 P[P[y]]、P[P[y]],…直到它们相同为止。对于图5(b)中的y与M[y]中的x,比较D[x]与D[y]不相同,表明区域Ⅱ由偶数个点组成。这时沿y的主路径y→n→m→s先返回一级到n→m→s,再与x的主路径x→m→s一起同时往回寻找,就能找到相同的起始点 m 并构建出封闭区域Ⅱ(x,y,n,m)。
2.4 算法过程综述
步骤:
1)计算所有线段和圆弧的交点,用交点和线段信息建立邻接表结构。
2)初始化每个节点 u。颜色值 COLOR[u]=白;距离值D[u]=无穷大;父节点P[u]=空;相遇点链表M[u]=空。
3)任意选取一点作为源节点 s。初始化 s:COLOR[s]=灰,D[s]=0,P[s]=空,M[s]=空。
4)将s加入先进先出队列Q。
5)只要Q中还有元素,取出Q队列的首元素u。
6)通过邻接表找到u的一个相邻的点v。
7)如果 v 为白色,设置 v 的值:COLOR[v]=灰,D[v]=D[u]+1,P[v]=u。然后将v作为新的一轮探索起点加入队列Q的尾部。
8)如果v为灰色,将节点u添加到v的相遇点链表M[u]中。9)如果v为黑色,跳过这一情形。
10)返回第6步,对u其余相邻的点作第 7)~9)这 3步的判断。
11)至此u的全部相邻点都已搜索完。将u的颜色COLOR[u]设为黑。返回第5步,对队列Q中剩余的点进行搜索。
12)至此源节点s所能达到的节点都已搜索过。如果还有点没有被探索,那么它是从s无法到达的点。选择这个未探索点作为新的源节点s,回到第3步进行新的遍历。
现在整个图都遍历过,所有节点都已为黑色,所有的封闭区域也已找到。以下步骤为输出这些封闭区域。
13)从所有节点中依次取出一个点u。
14)如果u的相遇点链表M[u]为空,那么返回13继续判断下一个点。
15)如果u的相遇点链表 M[u]不为空,那么从 M[u]中取出一个点v。新建一个含有节点信息的初始为空的双向链表L,用来存放构成封闭区域的点集信息。
16)如果D[v]等于D[u],则将u与v按次序加入双向链表L中。调用执行第20步。
17)如果 D[v]比 D[u]小 1,则将 u的父节点 P[u]、u与 v这3个点按次序加入双向链表L中。 取u=P[u],调用执行第20步。
18)至此双向链表L中已含有封闭区域边界上按顺序排列的点。返回执行第13步构建剩余封闭区域。
19)算法结束。每一个双向链表L含有一个封闭区域信息。
第 20)步以后为第 16)、17)步所调用执行。
20)如果父节点P[u]与P[v]为同一个点,那么把这个点P[u]加入 L 队首,返回调用处(16)或 17)步)。
21)取 u=P[u],v=P[v],再将 u 加入 L 队首,v加入 L 队末。返回执行第20步。
3 结果演示
图6(a)为读取含有线段圆弧信息的DXF文件后绘制的版图。对其应用本文的封闭区域分离算法后,再对封闭区域着色,结果如图6(b)。可以看到在本例中算法效果为去掉了布线部分,凸显出了板块布局。
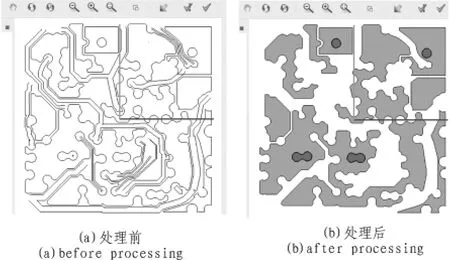
图6 封闭区域分离结果演示Fig.6 Presentation of the enclosed area separation result
4 结 论
本文介绍了一种封闭区域的发现算法。算法适应性强,只用给出二维平面中所有线段圆弧等基本元素的信息,就能够找出所有它们围成的任意形状的封闭区域。算法采用被广泛应用和证明了正确性的广度优先算法作为基础,这样最大化提高了算法的准确度和效率。应用在图形处理仿真软件中,为原本无法实现的任意封闭区域的选中,着色,切割合并等操作提供了快速可靠的解决方案。
[1]武运兴.二维图形内侧边界自动识别的研究[J].华北水利水电学院学报,1997,18(1):39-44.
WU Yun-xing.Research on automatic identification of 2D graphics medial border[J].Journal of North China Institute of Water Conservancy and Hydroelectric Power,1997,18 (1):39-44.
[2]杜月云,周子平,张云龙.一种任意多边形裁剪快速算法[J].计算机应用与软件,2009,26(6):265-267.
DU Yue-yun,ZHOU Zi-ping,ZHANG Yun-long.A quick algorithm for discretionary polygon clipping[J].Computer Applications and Software,2009,26(6):265-267.
[3]蔡志杰.一般多边形的切割[J].计算机辅助设计与图形学学,1998,10(3):248-252.
CAI Zhi-jie.General polygon cutting[J].CAD&CG,1998,10(3):248-252.
[4]陈瑞卿,周健,虞烈.一种判断点与多边形关系的快速算法[J].西安交通大学学报,2007,41(1):59-63.
CHEN Rui-qing,ZHOU Jian,YU Lie.Fastmethod to determine spatial relationship between point and polygon[J].Journal of Xi’an Jiaotong University,2007,41(1):59-63.
[5]Franco P P,Michael I S.Computational geometry:an introduction[M].New York:Library of congress, 1985.
[6]王舒鹏,方莉.混合积判断线段相交的方法分析[J].电脑开发与应用,2006,19(10):34-35.
WANG Shu-peng,FANG Li.An analysis of two segments intersection judgment with mixed product[J].Computer Development&Applications,2006,19(10):34-35.
[7]Thomas H C,Charles E L,Ronald L R.Introduction to algorithms[M].US:The MIT Press,1990.

