无穷小不可越“阶”

闫瑞玲

（大同大学浑源师范分校， 山西 大同 037400）

引言

在数学分析中，有不少计算和判断的问题的结论都与无穷小的阶数的高低有关。但初学者很难弄清楚怎样来把握这个“阶数”。本文以各实例从正反两个方面来分析如何正确地寻找合适的无穷小的阶，以得出正确的结论。

数学分析是数学系的一门基础课，以极限为主要研究方法，无穷小是一种特殊的极限。

无穷小有一些相关概念，分别是一阶（标准）无穷小、无穷小的阶数、高（低）阶无穷小。

不同的无穷小量收敛到“0”的速度有快慢之分，无穷小的阶数越高，收敛到“0”的速度越快。数学分析中有许多和无穷小的阶关系密切，如果越“阶”就会出错！下面的几个问题逐步说明。

一、极限的计算问题。

看课本上的一个习题：当a，b为何值时，

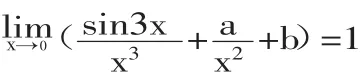
a=3，b=1.

误解原因：sin3x～3x仅仅是一阶近似公式，而分母的最高次项是3。造成错误的原因是用错无穷小的阶。

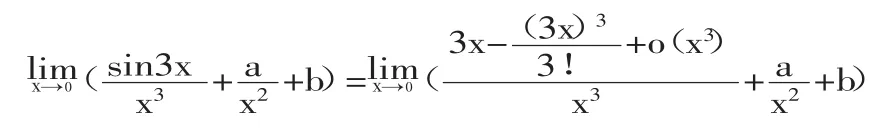
可以把题目修给为：

例1问a与b取何值时，

所以分子必为分母的高阶或同阶的无穷小。

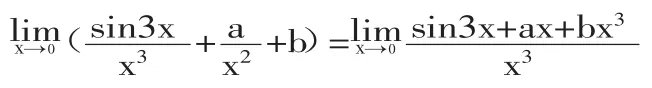
结合已知条件，有a=-3，

（若a≠-3，则一次项系数不为0，此时分子式分母的低阶无穷小，与题意相悖。）

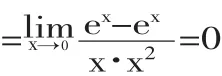
误解原因：除 x 外的其他形式（ex，etanx，tan2x）都是无穷次多项式，用错无穷小的阶。

正解：先求 ex，etanx，tan2x 的表达式，再代入计算。

解释一下，所谓“合适的表达式”就是对分子和分母找到合适的无穷小的阶。

同阶无穷小量在正项级数和无穷积分的敛散性判别法中有广泛的使用，若用错阶，就得不到正确的结论。

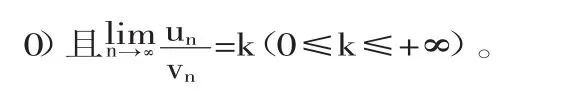
法则1）显然是同阶无穷小量性质的一个应用，法则2)中，由知 un=o（vn）（n→∞）

这是由高阶无穷小量判敛。法则3)是低阶无穷小量的性质。

[1]华东师大数学系.数学分析[M].

[2]钱吉林.数学分析解题精粹[M].