基于单体型重建的一种改进启发式聚类算法研究

侯 锟

（吉林师范大学 计算机学院，长春 136000）

0 引言

如今，随着时代的发展，科技的进步，生物工程建模已成为计算机理论及应用领域内最具吸引力、最具挑战性的一个方向之一。随着人类基因组图谱的基本完成[1]，人们对遗传的差异性、由基因突变引起的疾病复杂性有了更精确的阐释[2]。现在人们普遍认为，DNA序列中少数的差异是导致遗传疾病的主要原因。单核苷酸多态性(SNPs)，DNA某一位置碱基的变化[3]，被认为是一个物种不同个体表型的主要遗传来源[4]。研究SNPs对基因的研究、遗传疾病的诊断和药物研制有着重要作用。

现存研究成果主要集中与相关理论研究。依赖于不同的数据错误类型，主要有几种不同的解决模型。其中主要有最少片段删除模型、最少SNP去除模型和另外一种被普遍应用的模型、最少错误纠正模型。其中MER模型首先被Lippert等人证明是NP-hard问题[5]。实际上单体型重建问题可以被看作是一个聚类问题，这便是本文的落脚点。

本文首先将分析并给出单体型重建问题的形式化描述，设计一些必要的字符、公式定义。参考现存相关研究成果，提出另外一种基于k最近邻算法和粒子群优化算法的具有较好结果和效率的启发式的聚类方法。进行针对性的数据模拟实验，验证所提出算法的科学性与高效性。

1 单体型建模过程分析

SNP位点是一个物种的基因组DNA序列中不同个体可能出现不同碱基的位置。位于一个SNP位点的碱基称为等位基因。对于任意一个SNP位点来说，若两条同源染色体上的碱基相同，则称为纯和位点；若不相同，则称为杂合位点。几乎所有的SNP位点上的碱基都只有两种取值，为方便起见，我们用字符集{0,1,-}上的字符序列来表示单体型，而不必用真正的碱基字符，其中“-”表示该位点的取值未知，被称为空。因此单体型可看作是一个字符串序列。

人类的DNA序列是按染色体成对出现的，每一条染色体上SNP位点上的碱基序列叫做单体型，所以人类等二倍体生物都有一对单体型。在医学研究中，单体型数据通常比单个SNP携带更多的信息。基于单体型在遗传分析上的重要性，现在人们较为关注的是单体型的检测问题。

2 基于k最近邻和粒子群优化的聚类算法

2.1 单体型模型构建

定义P=(C1,C2)，集合C1和集合C2描述了片段划分到的两个集合。定义h1=(h11,h12,…,h1n)和h2=(h21,h22,…,h2n)为一对原始的单体型，用h'=(,)表示通过算法构造的单体型。用算法对片段进行分类后，可以通过叠加同一集合中的片段构造h1'。

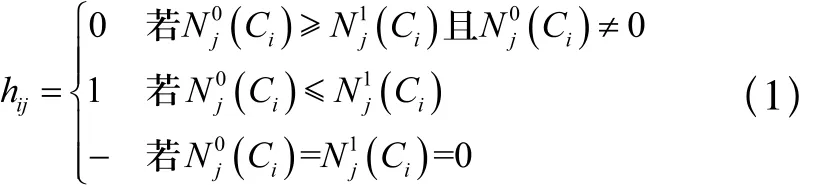
其中：i∈ (1,2)，j=1,2,…,n。

最后，用重建率(RR)来衡量单体型重建的正确度。重建率说明了重新构建的单体型h'=(,)与原始单体型h=(h1,)之间的相似程度。定义如下：

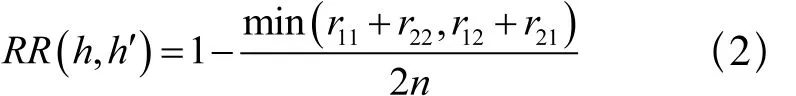
其中：rij=D(hi,)，i=1,2；j=1,2， 并且有：

2.2 改进算法分析

本文所提出的算法思路是基于粒子群算法与k最近邻分类算法的。其中，粒子群优化算法是近年来发展起来的一种新的进化算法。PSO算法和遗传算法相似，也是从随机解出发，通过迭代寻找最优解；也是通过适应度来评价解的品质，但比遗传算法规则更为简单，本算法没有遗传算法的“交叉”和“变异”操作，本算法通过追随当前搜索到的最优值来寻找全局最优。与遗传算法相比较，粒子群算法在大多数情况下，能较快的得到最优化的解。

k最近邻分类算法，是较成熟和较简单的聚类分析算法之一。该方法的思路是：选取一个待分类样本在特征空间中的k个最相似(即特征空间中最邻近)的样本，如果这k个中的大多数样本属于某一个类别，则该待分类样本也属于这个类别。

2.3 改进算法描述

将粒子群算法和部分的k最近邻算法结合起来达到优化结果的目的。

首先，计算出任意两条SNP片段之间的距离，找出距离最大者，并将相对应的两条片段分别放到集合C1和C2中，作为集合划分的初始值。接下来，在每次分配过程中，通过粒子群算法为未划分的每一条片段分别从集合C1和C2中选取k'条片段。其中k'的取值可由以下公式决定：

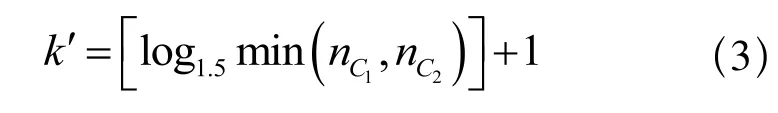
3 实验设计与结果分析

试验中采用真实数据和模拟数据来检验算法的准确性。并在四核中央处理器、内存最低为2GB的微机系统上用Java语言运行。

3.1 模拟数据实验

首先，用模拟数据来测试本文提出的改进算法。首先，随机生成10条不同的单体型，每条单体型长度为60，并通过相似度参数s来生成对应的10条单体型，其中：

s表示一对单体型中两条单体型之间的相似度。然后采用著名的shotgut测序模拟数据生成器Celsim来生成实验所需片段。通过设置参数片段数m=100；s=0.5；SNP缺失率g分别为0.25；0.5和0.75；错误率e分别为0.1，0.2，0.3，0.4来产生每对单体型的12个实例。然后用以上相同的参数设置，除了s设置为0以外，产生另外120个实例。改进算法运行模拟数据的结果显示在图1中，纵坐标代表重建率(RR)，横坐标代表错误率(e)。

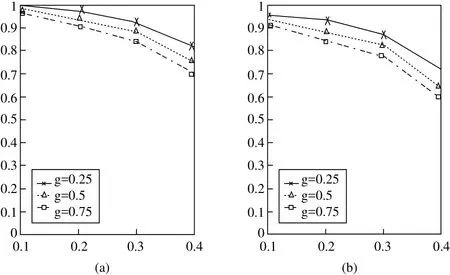
图1 不同参数下改进算法的重建率

图1中的(a)、(b)图分别是针对相似度参数S=0.5和S=0时，该算法在不同的错误率，不同缺失率下相对应的结果。图1表明单体型之间的相似度越高，重建率越高。同时也表明随着片段错误率、SNP缺失率的增大，算法的重建率逐渐降低。

3.2 真实数据实验

实验中用到的真实数据采用来自公开数据库的真实的单体型，该数据来自于国际人类基因组单体型图计划2006年7月发布的数据文件件中包含了CEPH样本(祖籍是北欧或西欧的美国犹他州人)中60个个体的单体型，每个单体型有SNP位点193,333个，本文实验随机选择一个个体指定长度的一对单体型。

本文采用著名的shotgun测序模拟数据生成器Celsim来生成实验所需片段。其中所需设置的参数 m：40，160，300；g：0.25，0.5和 0.75；e：0.1，0.2，0.3，0.4。表1是利用真实数据，在相同的条件下，把本文提出的算法与现存聚类算法进行比较的实验结果。

从表1中可以看出，在相同的缺失率、错误率的情况下，本文提出的算法能得到更好的实验结果。尤其是在错误率很大的情况下，该算法较现存算法依然能取得较好的实验结果。

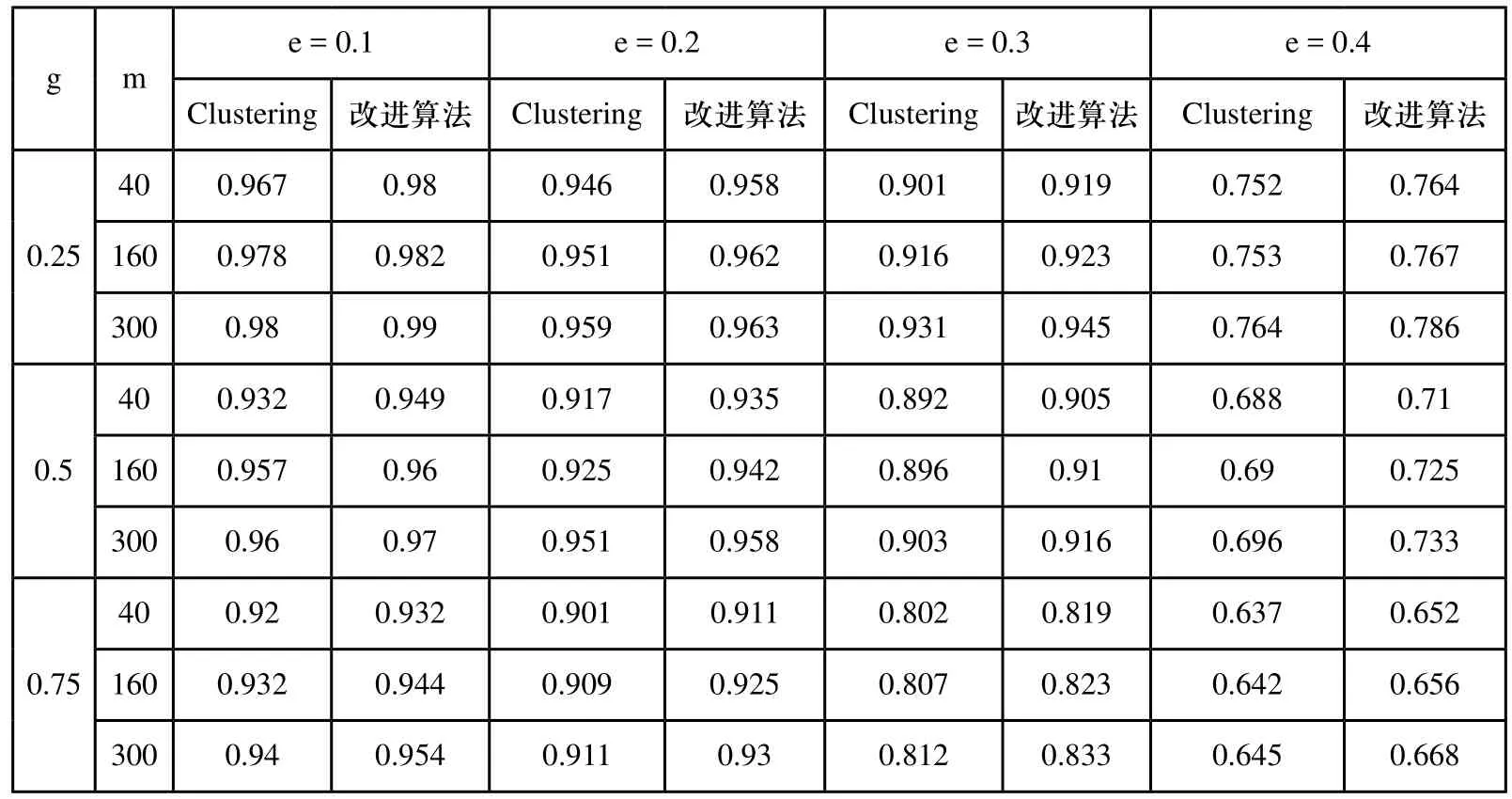
表1 现存算法与本文提出改进算法的结果比较

4 结束语

本文设计了一种启发式的数据聚类算法，从两个集合中同时选择k1条片段作为片段划分的依据是对现存相关聚类算法的改进，通过采用模拟数据和真实数据检验了改进算法的有效性。实验结果表明，该改进算法能取得更好更精确的结果，同时也提高了执行效率。

[1] The International HapMap Consortium. A haplotype map of the human genome. Nature, 2005, 437: 1299-1320.

[2] Z. Li, W. Zhou, X. Zhang and L. Chen. A parsimonious tree-grow method for haplotype inference. Bioinformatics,2005, 21(17): 3475-3481.

[3] R. S. Wang, L. Y. Wu, Z. P. Li and X. S. Zhang. Haplotype re-construction from SNP fragments by minimum error correction. Bioinformatics, 2005, 21(10): 2456-2462.

[4] X. S. Zhang, R. S. Wang. Models and algorithms for haplotyping problem. Current Bioinformatic, 2006, 1(1):105-114.

[5] 杨广文, 郑纬民, 王鼎兴, 等. 一种有效的启发式聚类算法[J]. 电子学报, 1999,27(2): 90-91.

[6] 金萍, 宗瑜, 李明楚,等. 共有信息引导的启发式聚类算法[J]. 计算机工程与应用, 2010, 46(31):50-53, 71. DOI:10.3778/j.issn.1002-8331.2010.31.014.

[7] 徐选华, 范永峰. 改进的蚁群聚类算法及在多属性大群体决策中的应用[J].系统工程与电子技术, 2011, 33(2):346-349.