阿基米德螺线拟Bernstein基最佳阶数的确定

马 翠，程攀科，周先东，刘悦宁

(1.第三军医大学 a.数学教研室;b.学员旅13队，重庆 400038;2.重庆市垫江县人民武装部，重庆 408300)

CAGD/CAD系统是通过用多项式曲线或曲面来表示零件的形状，进而精确地制造出零件。阿基米德螺线是CAGD/CAD系统中很重要的几何对象，但阿基米德螺线是空间 {1，sint，cost，tsint，tcost}中的曲线［1-5］，因此不能在CAGD/CAD系统中直接利用。通过用拟Bernstein基来表示阿基米德螺线，进而构造出多边形来控制阿基米德螺线，可使其在CAGD/CAD系统中得到很好的利用。由于阿基米德螺线的精度随其拟Bernstein基阶数的增加而增加，而现有的文献只考虑到5阶的情况［6-7］，不一定满足高精度的要求，因此对n阶的情形进行研究具有实际意义。本文通过对n阶情形的讨论，得到相应的多边形的顶点通式，从而确定了多边形。工业生产时，综合考虑经济因素和实际价值得到对应的精度，进而利用多边形的顶点通式及面积差值法即可确定拟Bernstein基的最佳阶数。运用阿基米德螺线来构造凸轮［8-10］，可使凸轮更加接近理想形状，从而体现了阿基米德螺线的实际意义。

1 阿基米德螺线的表示

设R、Q是阿基米德螺线上的2点，O是极点，并且∠ROQ=α，则α是弦RQ对应的张角，其中弦长如图1所示。

阿基米德螺线在直角坐标系中表示为

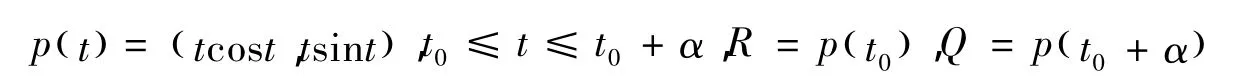
图1 阿基米德螺线的确定

2 拟Bernstein基的确定

由于阿基米德螺线必须要在多边形的控制下才能在CAGD/CAD系统中很好地利用，故接下来首先讨论确定多边形所需要的拟Bernstein基及其相关性质。定义拟Bernstein基的初始基［6-12］如下:

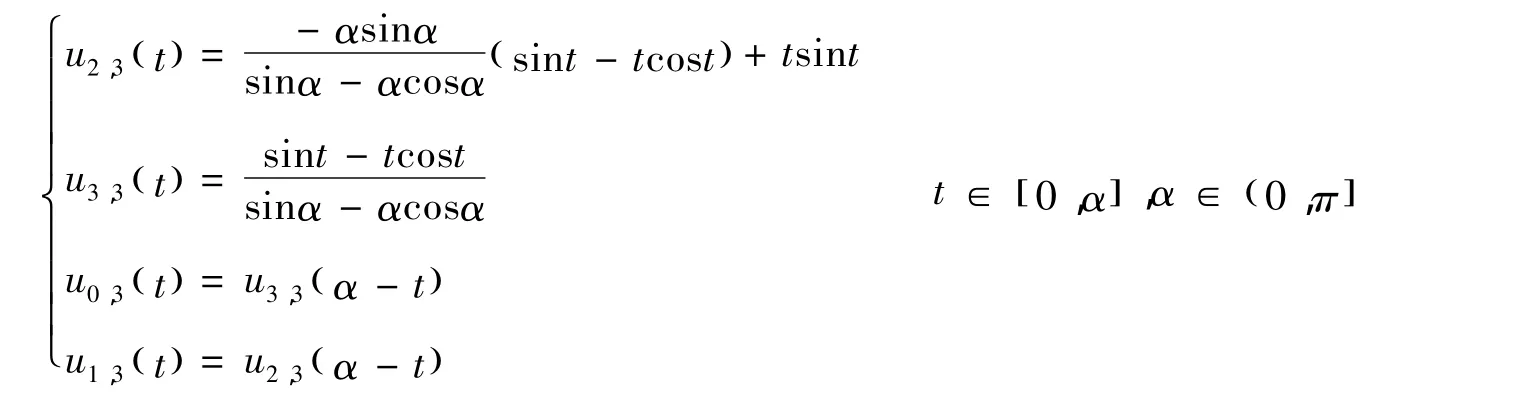
当n≥4时，由文献［8-12］可知:

拟Bernstein基具有如下性质［6-10］:

性质1 端点性质:0 是 ui，n(t)的 i阶零点，α 是 ui，n(t)的(n-i)阶零点，即{ui，n(t)}ni=0在端点处满足:

性质2求导公式

3 多边形的确定

由拟Bernstein基及其相关性质，可推出多边形的顶点表达式，即确定多边形。在直角坐标系中，阿基米德螺线的参数方程可表示为

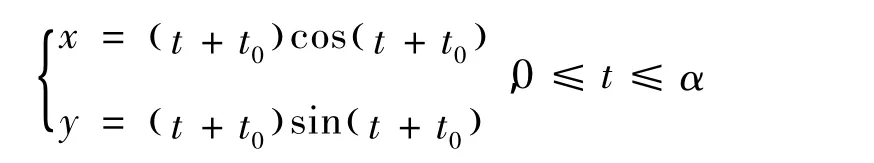
对文献［6-7］中的结论进行拓展，即可得到阿基米德螺线的n阶拟Bernstein基，表示为

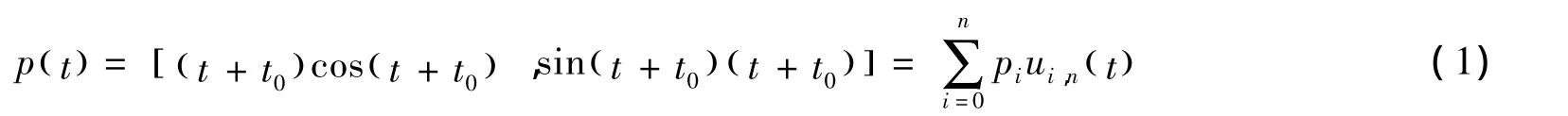
当t=0和t=α时，分别对式(1)求1，2，…，n阶导可得:

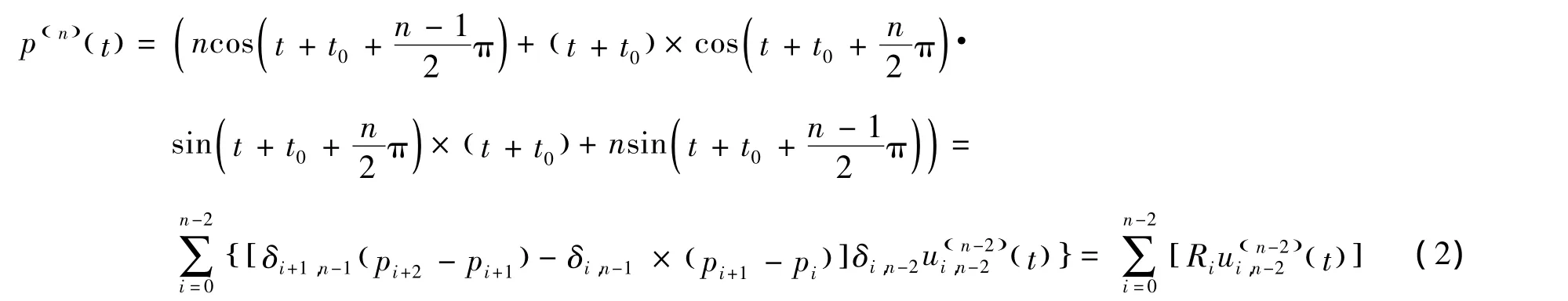
由式(2)可得到用n阶拟Bernstein基表示的阿基米德螺线的多边形顶点的通式为

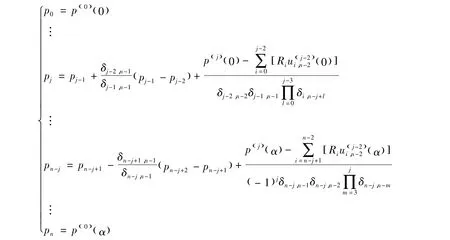
得到多边形的顶点后，利用文献［6］中所述多边形的画法及向量与向量夹角的相关性质，即可确定在n阶拟Bernstein基表示下所得到的多边形。

4 阿基米德螺线拟Bernstein基最佳阶数的确定

阿基米德螺线的精度是随其拟Bernstein基阶数的增加而增加的。从工业生产加工成形的经济性角度出发，在满足精度要求的前提下，确定最佳阶数具有重要的实际意义。

本文以张角为α，弦长为l的阿基米德螺线为例，讨论其拟Bernstein基从4阶向5阶增加时，求出相应的精度，进而推导出求精度的公式。

针对同一段阿基米德螺线，S0是定值，因此拟Bernstein基的阶数由4阶变为5阶后阿基米德螺线的精度

进一步推广，当拟Bernstein基由k阶变为(k+1)阶时，只需将S0求出，即可求得阿基米德螺线的精度

通过上述推导方法(即面积差值法)，在给定精度条件下，即可得到相应阿基米德螺线的拟Bernstein基的最佳阶数。

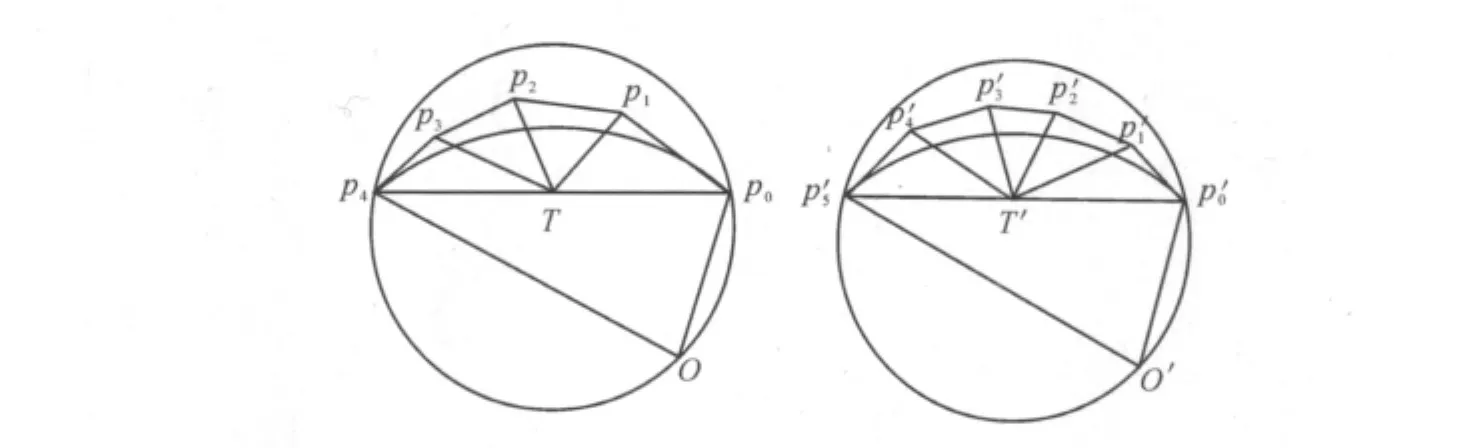
图2 控制4阶和5阶的阿基米德螺线的拟Bernstein基的多边形图形

5 实例验证

阿基米德螺线在CAGD/CAD系统中最重要的运用就是构造凸轮［6-10］。本文利用的一段阿基米德螺线进行凸轮的构造。利用本文方法求出在不同阶的拟Bernstein基表示下的控制该段阿基米德螺线的多边形的顶点，并确定多边形，进而利用面积差值法计算出相应的精度。如表1所示。

从表1明显看出，阿基米德螺线的精度随拟Bernstein基阶数的增加而增加。本文以95%的精度为例，选取相应阶数的拟Bernstein基表示的阿基米德螺线(即7阶)用于构造凸轮。

表1 不同阶数表示的精度

首先画出用7阶拟Bernstein基来表示的阿基米德螺线;然后作出一条与其呈纵轴对称的阿基米德螺线，并连在一起;最后再作出与该2段阿基米德螺线呈横轴对称的曲线，并连在一起，从而构造出凸轮(图3)。

6 结束语

讨论了用n阶拟Bernstein基来表示阿基米德螺线所得到的多边形顶点的通式，进而确定多边形;同时利用面积差值法推导出了在各阶拟Bernstein基表示下的计算阿基米德螺线的精度的公式，从而在给定精度的条件下，确定阿基米德螺线的最佳拟Bernstein基的阶数。实例验证表明，本文的研究具有明显的实际意义。

图3 凸轮及其控制多边形

［1］ZHANG Jien.C-curves:an extension of curves［J］.ComputerAided Geometric Design，1996，13(3):199-217.

［2］MAINAR E，PENA J M，SANCHEZREYES J.Shape preserving alternatives to the rational Bezier model［J］.Computer Aided Geometric Design，2001，18(1):37-60.

［3］胡晴峰，汪国昭.双曲混合多项式形式的Ball曲线［J］.浙江大学学报:理学版，2004，31(6):625-630.

［4］JIN Yiming，WANG Guozhao.Generation and properties about quintic C-Bézier curves［J］.Applied Mathematics A Journal of Chinese Universities Serial A，2005，20(1):91-96.

［5］Paolo Mancosu，Andrew Arana.Descartes and the cylindrical helix［J］.Historia Mathematica，2010，37(1):403-427.

［6］张瑞坤，汪国昭.阿基米德螺线的拟Bernstein基表示［J］.计算机辅助设计与图形学学报，2006，18(7):918-923.

［7］张瑞坤，汪国昭.阿基米德螺线的拟Bernstein基表示［J］.浙江大学学报:理学版，2007，34(2):163-167.

［8］张永岗，姚文席.阿基米德螺线超越离合器的楔角研究［J］.机械工程师，2007，10(11):17-18.

［9］Triantafyllidis G K，Stefanidis N G.Fracture Characteristics of Tensional-Torsional Fatigue Failure of Archimedes Helix［J］.J Fail Anal and Preven，2011，11(1):222-226.

［10］Xinhon Xiong，Haiou Zhang，Guilan Wang，et al.Hybrid plasma deposition and milling for an aeroengine double helix integral impeller made of superalloy［J］.Robotics and Computer-Integrated Manufacturing，2010，26(1):291-295.