有毒素时两竞争鱼群的独立捕获问题
杨海霞
(甘肃联合大学师范学院,兰州 730000)
加拿大著名生态经济学家Clark.C.W[1]在研究可再生资源的最优管理问题方面作出了比较突出的贡献,他系统地阐明了人类对生物种群的开发应追求经济利益和环境利益的统一,这样才能实现可持续发展。毒物对生态群落的影响成为最近几十年人们所关心的主要环境问题之一。海洋环境下的关于生态毒理学问题的数学研究已经开始。最近学者们对由海洋生物种群自己释放的毒物产生的生态毒理学效应很感兴趣[2-3],已成为水生态的一个主要研究方向。Shukla等[4]对这类生态毒理学问题建立数学模型,并研究了毒物对生物种群的影响。
由文献[2-3]知,在一个两种群竞争的Lotka‐Volterra系统中,Maynard Smith加上了毒素物质作用这一项,并且假设只有当对方存在时每个种群就都会向对方释放一种毒物来阻止对方的生长。受文献[2-3]的启发,文献[5]将Maynard Smith的思想推广到两竞争的鱼群中,研究了毒素环境下对两竞争鱼群之一进行捕获的优化问题。本文将进一步研究对两竞争鱼群进行独立捕获的最优策略问题[6-7]。
1 模型的建立
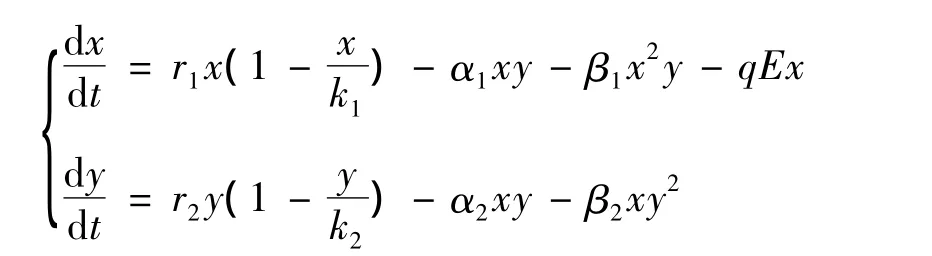
对文献[5]中的模型进行修正,假设两鱼群都遵守Logistic增长规律,且服从的是独立捕获模式,此时增长方程可以写为
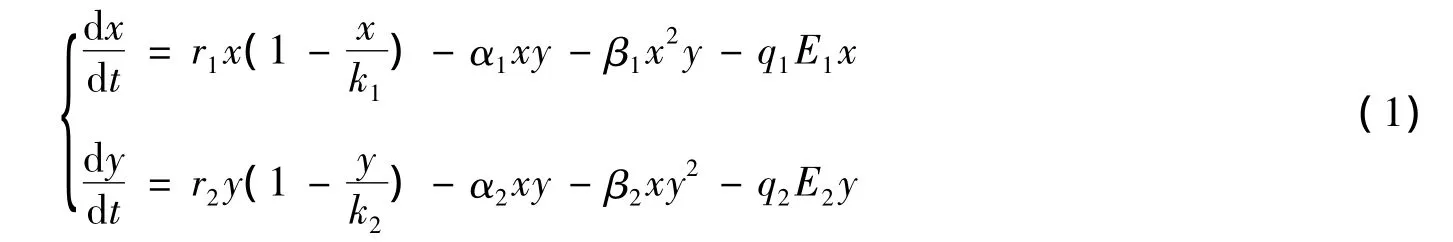
其中:x(t)、y(t)代表两竞争种群在任一时间的 t时刻的种群密度;r1、r2、α1、α2、β1、β2、k1、k2都是正常数;r1、r2代表两种群的内禀增长率,k1、k2是它们的环境容纳量;β1、β2分别是y种群对x种群和x种群对y的毒素作用系数。两种群为了一个外部食物资源而相互竞争,在没有对方时,每个种群都按Logistic增长规律增长。r1/k1和r2/k2是种内竞争系数。β1x2是y种群对x种群密度的一种功能反应,它来自于由y种群为阻止x种群食用共同的的食物资源而产生的一种毒素物质。因为d(β1x2)/dx=2β1x>0和d2(β1x2)/dx2=2β1>0,所以当竞争对手越多时,此种群释放毒素的速率会增大。β2y2可以进行类似的解释。
这种捕获方式是用E1的努力量捕获x种群,用E2的努力量捕获y种群。两种群分别进行捕获。其中q1、q2是两种群的捕获能力系数,q1E1x和q2E2y称为捕获率函数。
2 平衡点及其性态分析
系统(1)可能的平衡点是
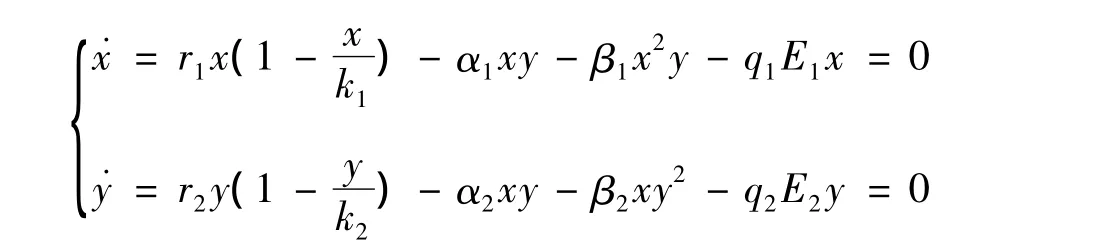
的解,即
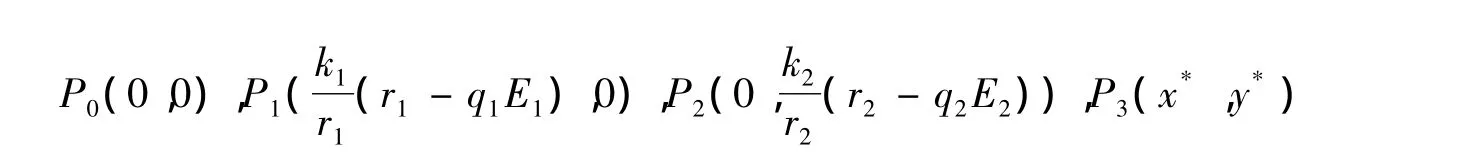
其中点P3(x*,y*)满足方程组:

以下对平衡点稳定性的分析依据的是常微分方程定性理论知识[8],推导过程类似于文献[5]中对平衡点稳定性的分析。内禀增长率r和捕获能力系数q之比r/q称作是种群的BTP,因此,BTPx=r1/q1,BTPy=r2/q2。
定理1 E1>BTPx,E2>BTPy,则平衡点 P0(0,0)是系统(1)的一个稳定结点;若 E1> BTPx,E2<BTPy,则平衡点 P0(0,0)是系统(1)一个不稳定的结点;若 E1< BTPx,E2< BTPy或者 E1< BTPx,E2>BTPy,则平衡点P0(0,0)是系统(1)一个鞍点。
定理2 设
定理3 设
定理4
1)若毒素系数比 β1/β2满足,则系统(1)的正平衡点P3(x*,y*)是局部渐近稳定的。
2)若毒素系数比β1/β2满足或,有A1x*+B1y*+C1>0成立,则系统(1)的正平衡点P3(x*,y*)是局部渐近稳定的。其中:
证明在证明平衡点P3(x*,y*)的局部稳定性之前,首先说明正平衡点的存在性。
因为 P3(x*,y*)是


其中:
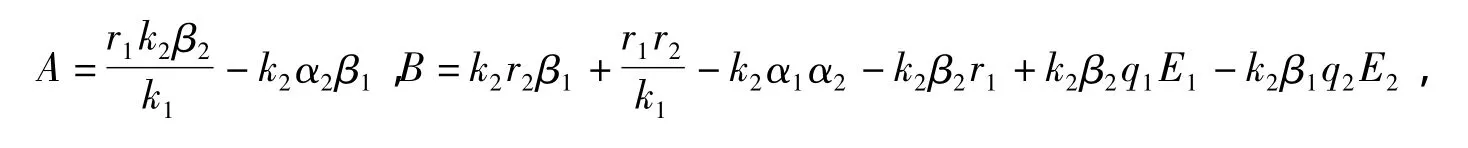
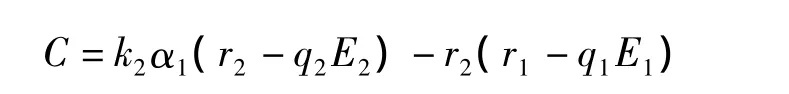
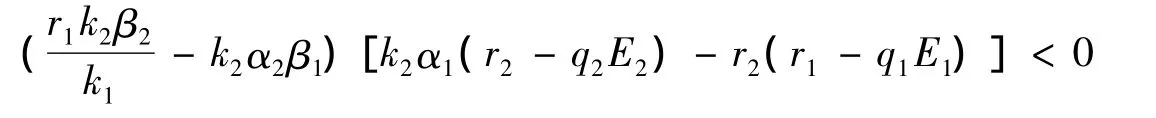
时,x*是上面这个方程的唯一正解。
由x*可得由y*的表达式可以看出,要使y*>0,只有即时,y*>0。当然,为保证x*>0,不等式r1-q1E1>0也应该成立。
由以上的分析知,当不等式
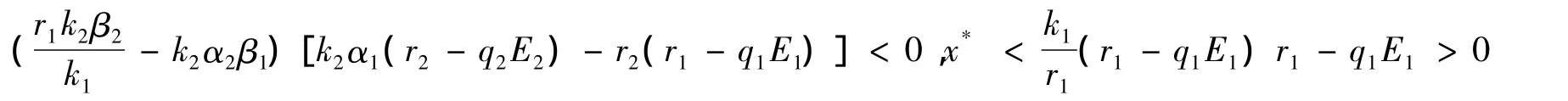
同时成立时,唯一的正平衡点是存在的。
正平衡点P3(x*,y*)的局部稳定性证明过程类似于文献[5]中定理1的证明。
通过上面的讨论分析,得到了以下重要结论:
结论1 毒素物质对动力系统的稳定性有影响,即两种群释放毒素的强度可以改变系统的稳定性(在无毒素释放时系统是不稳定的,而在有毒素释放时系统是可以变成稳定的)。
定理5 若条件成立,则系统(1)的正平衡点P3(x*,y*)是全局渐近稳定的。
此定理的生物意义是:对2个相互见面时释放毒素的竞争种群而言,即使对两种群进行独立捕获,但当参数满足一定条件时,系统不会出现周期振荡,两种群最终将保持在各自的平衡水平,持续生存。
定理6 系统(1)在第1象限内不存在极限环。
定理6表明:对2个相互见面时释放毒素的竞争种群而言,如果对两种群进行独立捕获,系统不会出现周期振荡现象。
定理7 从R2+出发的系统(1)的所有解是一致有界的。
定理7表明:系统有很好的生物性态,从R2+出发的系统的所有解轨线最终都会进入同一个区域内。
3 最优收获策略
在可再生资源的商业开发中,最基本的问题是在现在和将来的收获之间作出一个最优的决策。如果从同这个问题有关的政治社会和哲学领域都去研究的话,这个问题非常困难,可能无法解决。不过,如果仅从经济观点考虑此问题,就必须使用时间贴现这个基本工具来解决跨时间经济效益的问题,这在商业管理中是一种惯用的行为。Clark在文献[1]中证明了应用最大可持续经济租金这个概念是不现实的,因为它相当于使时间贴现率等于零。
要使种群资源开发有长期利润,就需要考虑怎样控制捕获量才能使得一定时间内捕获所得到经济收入最大,并且使种群保持一个正常的生长繁殖能力。因此,为决定一个最优收获策略,本文的目标是使一个连续时间段收入的现值(现值收入)达到最大,此现值由式(2)给出。

其中:J表示总收入的现值;δ表示瞬时年贴现率。此问题通过采用最优控制理论中的Pontryagin最大值原理来求解。
此问题可归结为如下最优控制问题
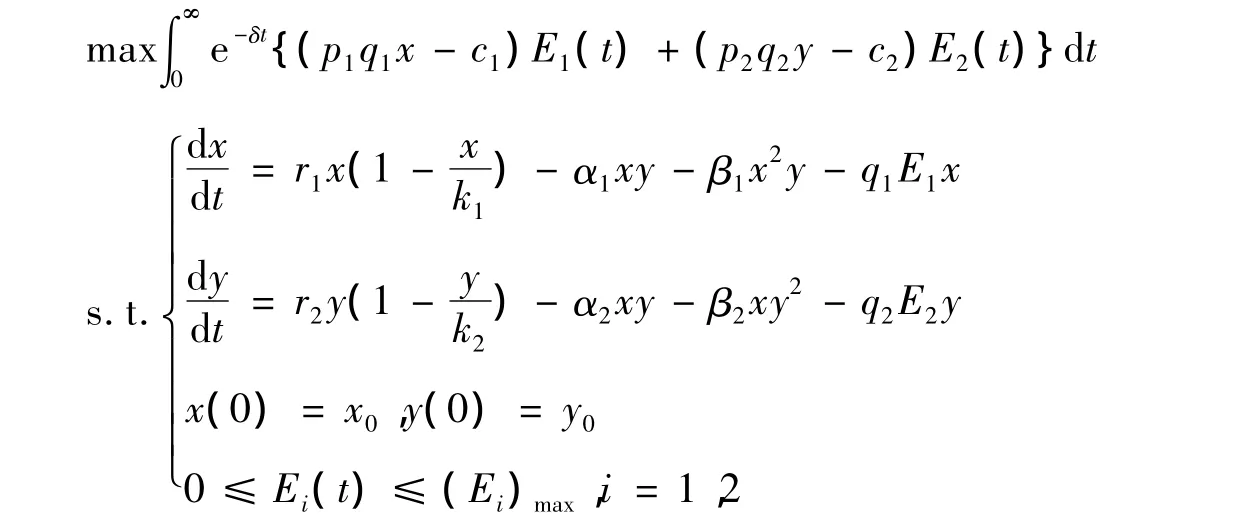
其中:x、y是状态变量;Ei,i=1,2是控制变量。
首先构建这个问题的Hamilton函数:
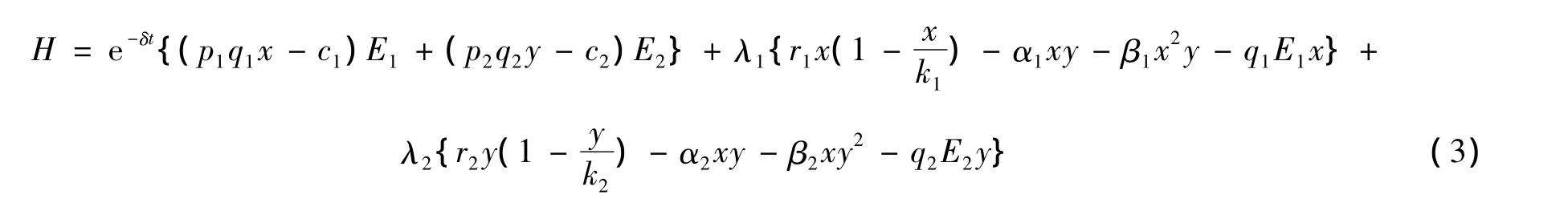
其中:λ1(t)和λ2(t)是伴随变量;控制变量E1、E2在Hamilton函数H中是线性的。
假设控制约束没有起到约束作用,也就是最优平衡点不会出现在(Ei)min或(Ei)max处,就必有奇异控制,它满足,于是有
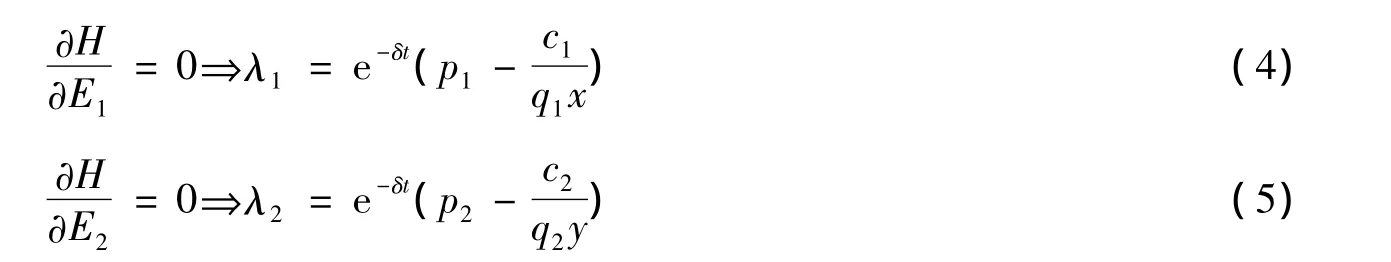
因此,由方程(4)和(5)可以看出影子价格e-δtλi(t),i=1,2在最优平衡点处不会随时间而变化。这样它们满足在无穷大处的横截条件,即当t→∞时,影子价格仍然有界。
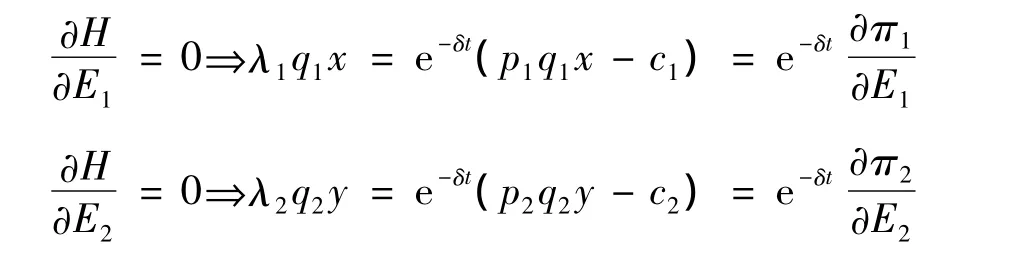
这表明了对每个种群而言,每单位努力量收获的使用者成本必须等于在平衡努力量水平下努力量将来边际利润的贴现值。
这里要导出这个问题的一个最优平衡解。因为要考虑的是一个平衡解,所以x、y、E1和E2在下面的计算步骤中按常数对待。
根据最大值原理,伴随变量λ1和λ2必须满足
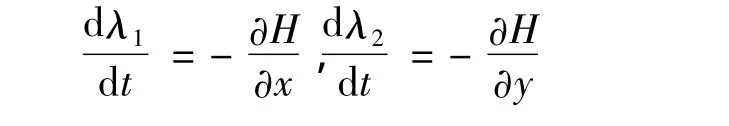
上面这组方程可以重写为
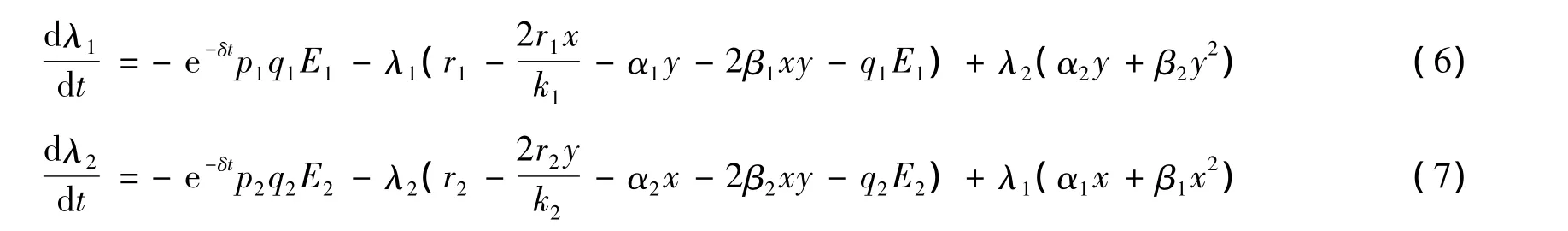
本文考虑的是最优平衡解,因此可以令˙x=˙y=0,从而有

将方程(4)、(5)和(8)代入方程(6),化简后有
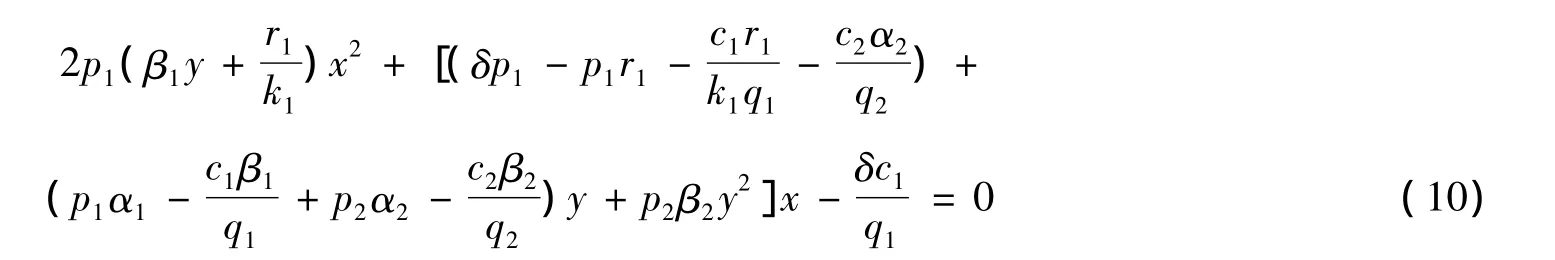
此方程可以看作是关于x的一元二次方程,很容易判断它存在一个正根。
同理,将方程(4)、(5)和(9)代入方程(7),经化简后有
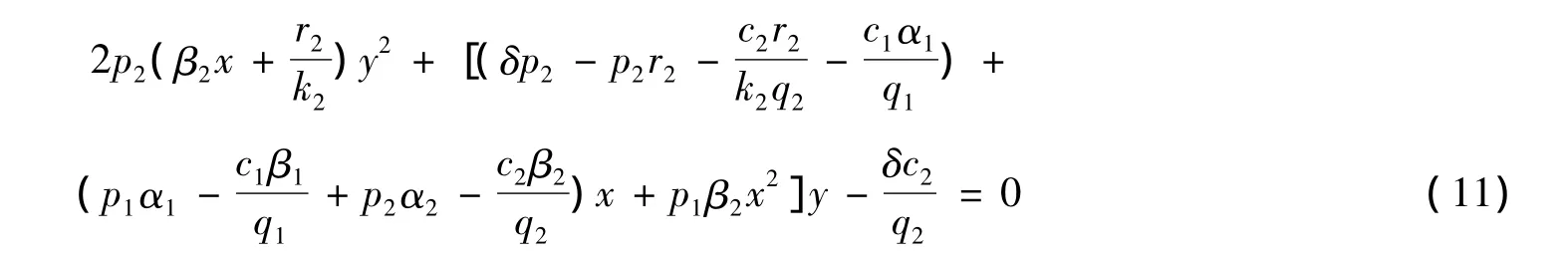
把这个方程看作是关于y的一元二次方程,经判断它存在2个实根,一个为负根,一个为正根。从生态意义考虑,仅对正根感兴趣。此正根为
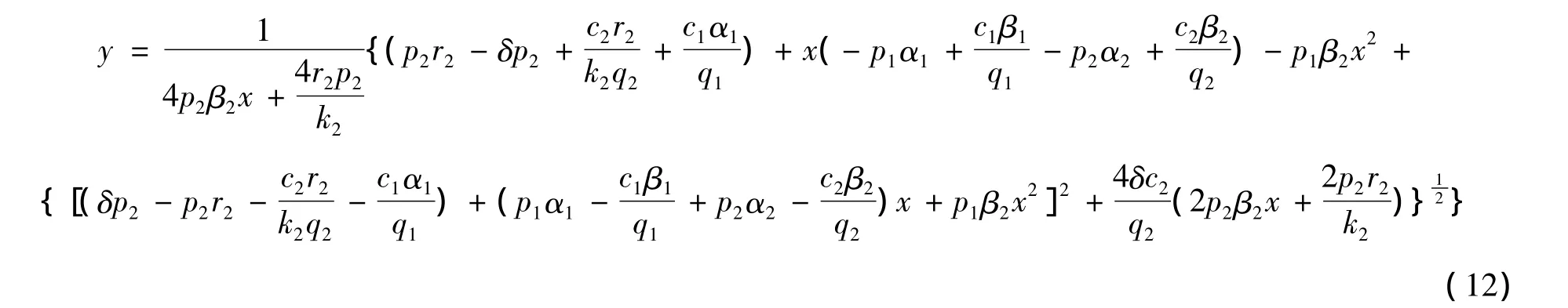
将方程(12)代入式(10),经化简后得
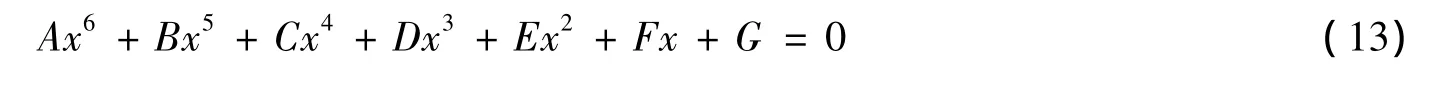
其中:
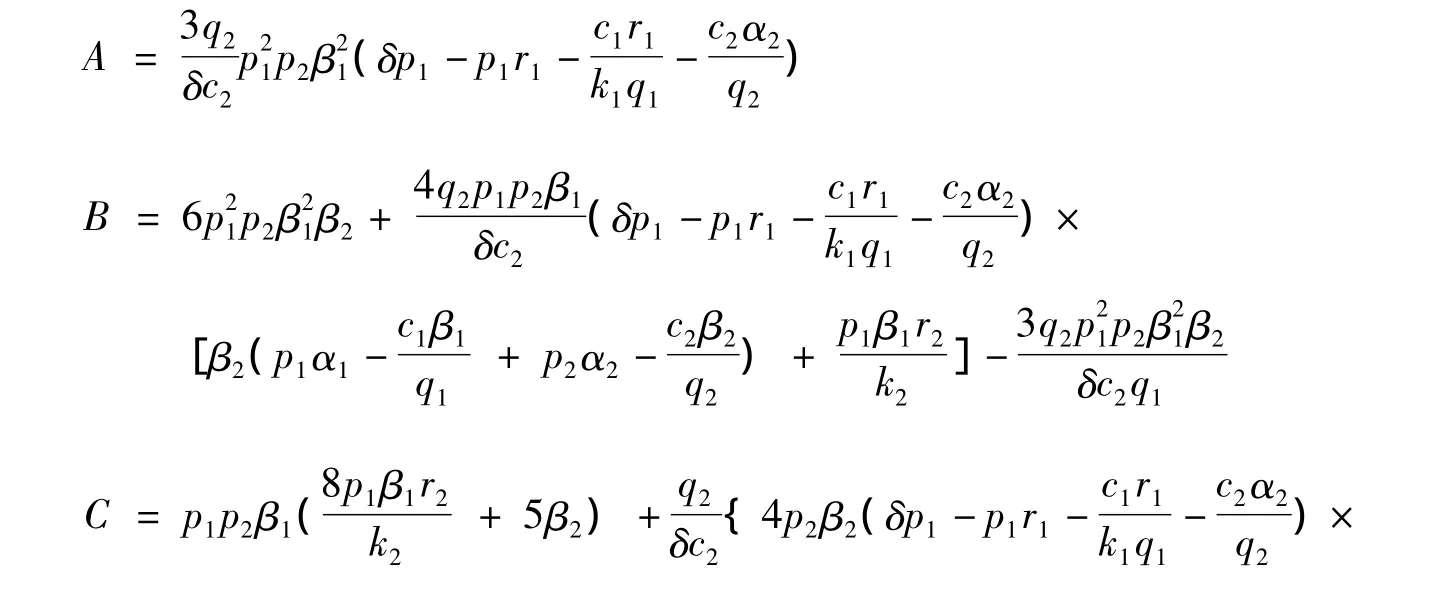

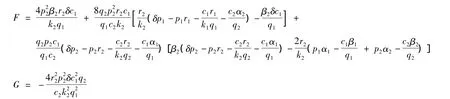
满足方程(13)的正解(如果存在)就是最优解x=x*,然后从方程(12)中可以得到y=y*,从而有
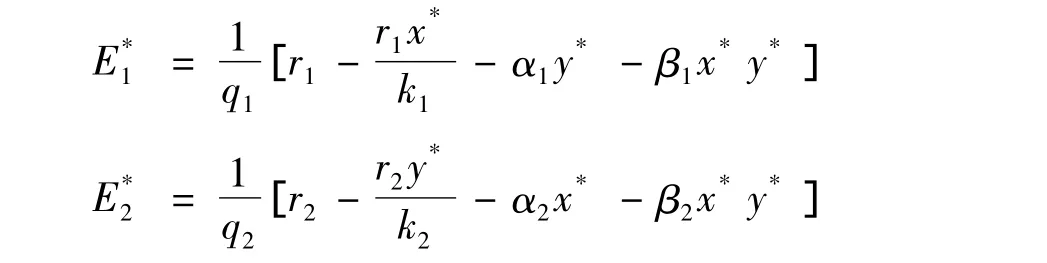
4 结论
无论是对两竞争种群进行独立捕获或是只对其中之一进行捕获,都得到了相似的结论:在一定条件下,可以保证两种群的持续生存;两种群释放毒素的强度可以改变系统的稳定性;毒素物质的释放对平凡平衡点和边界平衡点的局部稳定性没有影响;系统不会出现周期振荡现象;系统的所有解都是一致有界的;利用Pontryagain最大值原理得到了最优的捕获努力量和相对应的最优种群规模。
[1]Clark C W.Mathematical Bioeconomics,the Optimal Control of Renewable Resource[M].New York:John Wiley sons Inc,1990.
[2]Kar T K,Chaudhuri K S.On non-selective harvesting of two competing fish species in the presence of toxicity[J].Ecological Modeling,2003,161:125-137.
[3]Bandyopadhyay M.Dynamical analysis of a allelopathic phytoplankton model[J].Jorunal of Biological Systems,2006,14(2):205-217.
[4]Shukla J B,Agrawal A K,Dubey B,et al.Existence and survival of two competing species in a polluted environment:a mathematical model[J].J Biol Syst,2001,9(2):89-103.
[5]杨海霞.有毒素时两竞争鱼群的最优捕获策略[J].甘肃联合大学学报,2011,25(1):8-13.
[6]赵琳,雒志学,王利红.在容量较小的污染环境中种群的最优捕获问题[J].重庆理工大学学报:自然科学版,2011(2):122-126.
[7]倪春青,胡志兴.一类具有常数收获率的具有功能性反应捕食模型的定性分析[J].重庆工商大学学报:自然科学版,2010(3):235-239.
[8]马知恩,周义仓.常微分方程的定性与稳定性方法[M].北京:科学出版社,2001.

