双电压合成矩阵变换器的新型扇区划分
史明明 周 波 魏佳丹
(南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京市 210016)
1 引言
矩阵变换器是一种具有优良输入输出性能的直接交-交功率变换器,省去了大容量的中间直流储能环节,具有结构紧凑、功率密度高的优点,在工业应用中具有良好的前景[1,2]。
近年来由于功率器件的发展,双向开关Sij(i∈{u,v,w},j∈ {a,b,c})可通过采用两个具有逆向阻断能力的RB-IGBT(Reverse Blocking Insulated Gate Bipolar Transistor)反向并联而组成[3-5],降低了主功率电路的复杂度,如图1 所示。
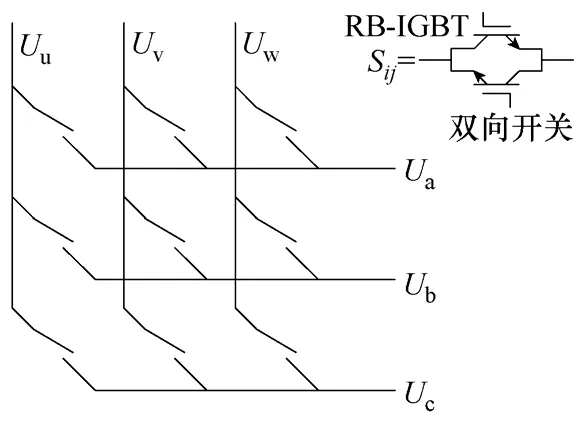
图1 矩阵变换器电路拓扑图Fig.1 Topology of matrix converter
在矩阵变换器的诸多控制策略中,最具有代表性的有双空间矢量调制策略与双电压调制策略。双空间矢量调制策略物理概念清晰,较好地表达了交直-交变换器的控制思想,文献[6-8]的研究工作推进了双空间矢量调制矩阵变换器的实用化进程,但双空间矢量调制对不平衡输入的抑制需要通过补偿的方式才能实现,增加了控制软件的计算复杂度。双电压调制策略能够在输入电压波动时,自动调节占空比,维持输出电压为期望值,并且在不平衡输入时能够进行自动补偿得到对称的输出电压,具有天然的抵抗不平衡输入的能力,在输入电压易受波动的应用中具有独特的优势,自从该方法提出后便受到了很多学者的关注[9-15]。
在双电压调制策略中,一般都要将每个周期输入电压与期望输出电压按照某种规律划分成多个时间段,称为扇区。传统的扇区划分原则是将输入与输出分别划分为6 个扇区,共计36 种扇区组合。文献[14]提出了一种18 个扇区的划分方法简化了双电压调制策略,但该方法在输出扇区划分中以输入相电压作为扇区判断变量进行划分,因此输入三相电压不平衡时该方法失效。为此,本文结合双电压调制策略的特点,利用输入线电压与相电压在扇区划分中的对应关系,通过引入表征相电压扇区特征的变量Y,以输入线电压作为扇区判断变量解决了文献[14]所提方法在不平衡输入时失效的问题,同时将输出线电压扇区数减少为3 个。
2 矩阵变换器双电压控制策略基本原理
双电压控制策略是通过选择两个合适的输入线电压合成期望输出线电压。设三相输入相电压为

式中,Uim为输入相电压幅值;ωi为输入角频率。
文献[12]给出了输入输出电压扇区的最佳划分方式,其输入电压的每个周期被划分成6 个扇区。原则是在每个扇区中输入线电压的最大值、中间值和最小值保持不变,可形象地称为S形扇区划分。
在一个扇区中的三个线电压可定义为Umax、Umid、Umin,如下所示
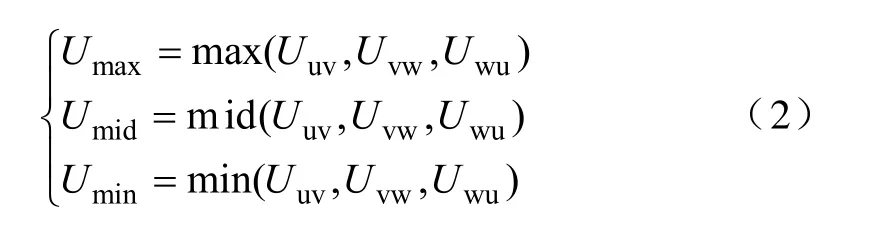
本文以Qi(Qi∈{1,2,3,4,5,6})作为输入电压扇区号标记,如图2 所示。
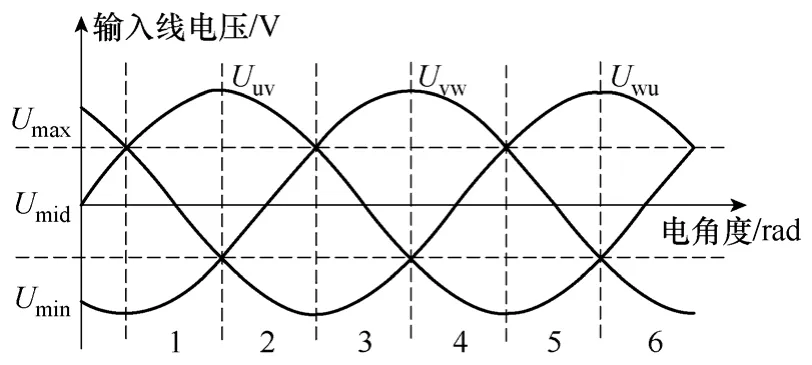
图2 三相输入电压扇区Qi 划分示意图Fig.2 Diagram of the input sectors Qi division
同样,设三相期望输出相电压为
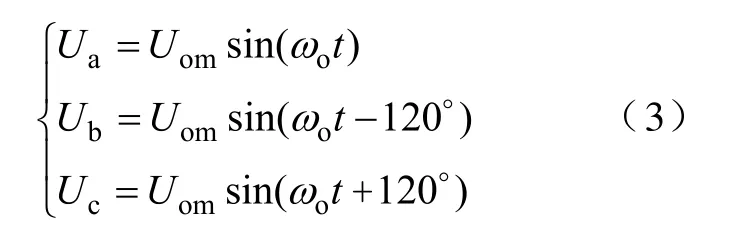
式中,Uom为输出相电压幅值;ωo为输出角频率。
在双电压控制策略中通常将期望输出电压的每个周期也划分为6 个扇区。输出扇区的划分原则是:同一扇区中,输出三相线电压的极性保持不变,可形象地称为X形扇区划分。输出电压扇区以Qo(Qo∈{1,2,3,4,5,6})作为扇区号标记,如图3 所示。

图3 三相输出电压扇区Qo 划分示意图Fig.3 Diagram of the output sectors Qo division
以扇区组合Qi=2、Qo=2 为例,此时期望输出线电压Uab、Uac、Ucb将利用幅值最大的两个输入线电压Uuv、Uuw进行合成,用Uuu输出零电压。具体的占空比计算在文献[9]中有详细推导,在此就不做赘述。
扇区划分的目的是规律化出每个扇区组合内的占空比计算公式。传统双电压控制策略中的输入输出扇区划分方法很直观,但该方法中存在36 种扇区组合,并且每个扇区组合中用于合成输出的两个输入线电压均不同,其实现过程较为复杂。为解决这个问题,本文提出一种新型扇区划分方法,将扇区组合数减少一半,并在此基础上推导出用于合成期望输出线电压的两个输入线电压的选取数学规则,简化了实现算法。
3 新型扇区划分方法
3.1 新型扇区划分规则
本文对于输入线电压的划分采用与文献[11]相同的S形扇区划分,由于线电压与相电压在相位上互差30°,因此输入线电压的S形扇区划分对应于输入相电压的X形扇区。
由双电压合成理论可知:当输入相电压的极大值相在一个扇区内保持不变时,此时合成期望输出极性均为正的两个线电压;当输入相电压的极小值相在一个扇区内保持不变时,此时合成期望输出极性均为负的两个线电压。
为了深入分析输入与输出扇区之间的关系,引入变量Y表征S形输入线电压扇区划分下对应相电压的特征:Y=1 表示输入相电压扇区的极大值在整个扇区内保持不变;Y=-1 表示输入相电压扇区的极小值在整个扇区内保持不变,如图4 所示。

图4 输入线电压扇区与相电压扇区划分 之间对应关系图Fig.4 Diagram of input sector relationship
由于矩阵变换器9 个开关均为双向开关,因此能够合成输出三相系统的任意6 个线电压,即Uab、Ubc、Uca、Uba、Ucb、Uac。Y值确定任一时刻合成输出的两个极性相同的线电压:Y=1 表示选择合成的两个期望输出线电压极性都为正,Y=-1 表示选择合成的两个期望输出线电压极性都为负。根据线电压极性同正或同负可以得到两种不同的扇区划分结果,如图5 所示。
图5a 所示的Y=1 情况下的120°扇区划分规则可由下式表示
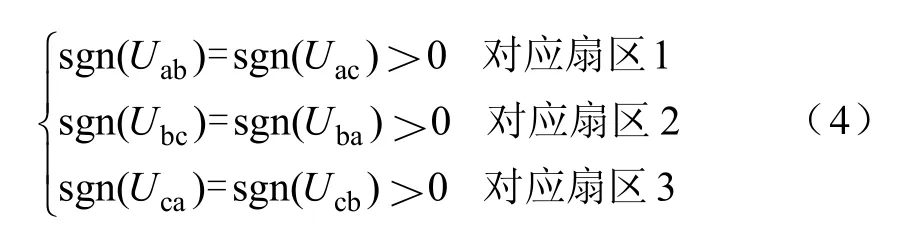
以图5a 中标号为1的120°扇区为例,Uab在120°内始终为正,Uca在120°内始终为负。由于Uca与Uac反相,则Uac在120°内始终为正,因此选择合成输出的线电压为Uab、Uac。同理,图5b 中Uab与Uac、Ubc与Uba、Uca与Ucb在120°扇区内极性为负的,对应于Y=-1的情况。
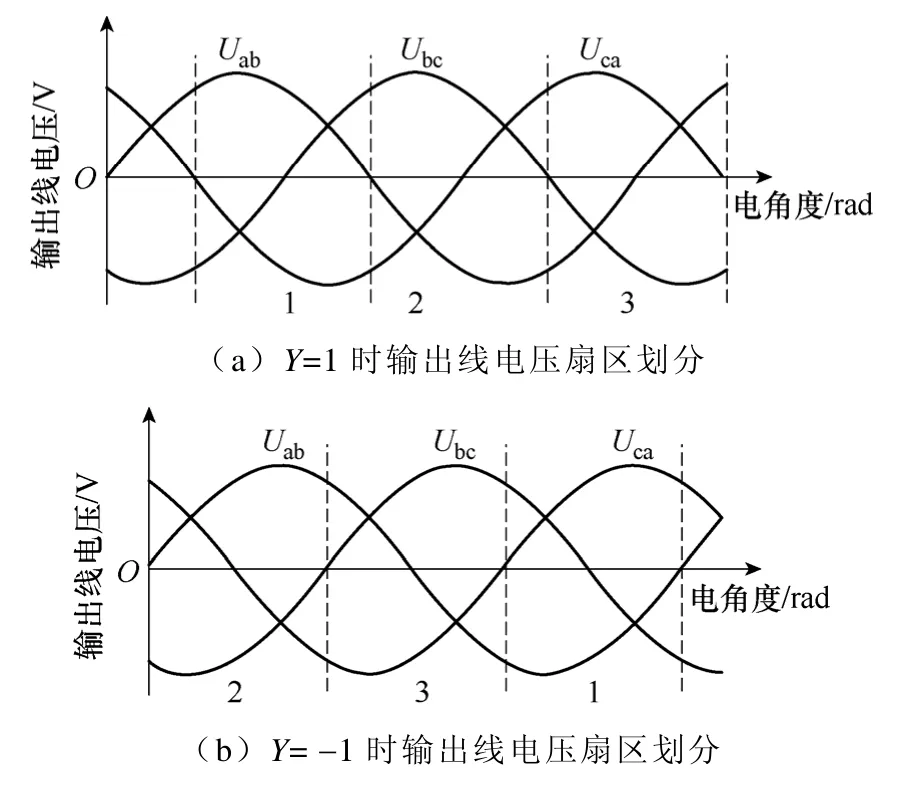
图5 输出线电压的120°扇区划分示意图Fig.5 Diagram of output sector with 120°region
为使Y=1 与Y=-1 两种情况下输出线电压扇区划分统一,将变量Y综合到输出线电压的判断规则中,得到最终用于扇区判断的数学表达式,如下所示
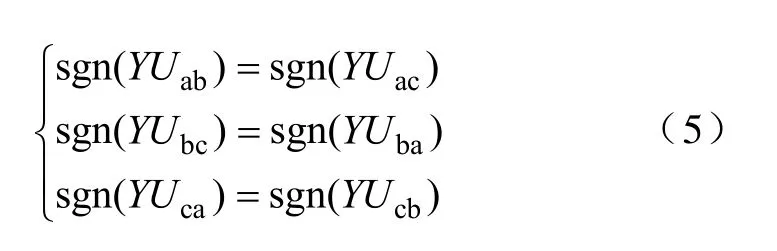
式(5)将图5a 和图5b 所示的Y=1 与Y=-1两种120°区域的输出线电压扇区模式统一在一个数学规则下,将输出线电压划分为3 个扇区,输出线电压扇区由6 种状态减少为3 种状态,输入输出扇区的组合数由36 种减少为18 种,简化了双电压的数字化实现。
3.2 新型扇区划分模式下占空比计算公式推导
通过对文献[9]传统双电压控制中占空比系数表达式的分析可知,占空比系数公式可分解为输入因子、输出因子以及常数因子k。
为使占空比计算公式更简单,本文将输入因子与输出因子均用恒大于零的表达式表示。输入因子可表示为(Umax,Umid)、(Umid,Umin),定义输出因子为U1、U2。U1、U2为选择期望输出的两个线电压的幅值,在不同扇区下的取值如下表所示。

表 输出线电压扇区所对应的变量取值Tab. Variables in different sectors of output voltage sector
通过上文的分析,归纳出新的扇区划分方法下通用的占空比表达式
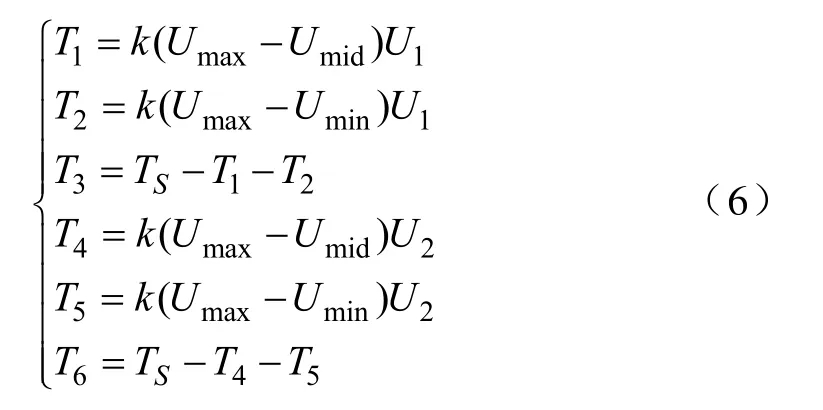
式中,TS为矩阵变换器的开关周期;T1~T6分别为所对应开关的导通时间。为减少开关次数,采用锯齿波作为载波进行调制,对应开关时间调制模式如图6 所示。

图6 开关时间调制模式示意图Fig.6 Diagram of switching pattern
为与矩阵变换器中双向开关Sij(i∈{u,v,w},j∈{a,b,c})定义一致,定义Ui表示输入扇区中取得极值的相电压,Ui-表示超前Ui相120°的相电压,Ui+表示滞后Ui相120°的相电压,Ui,i-、Ui,i+分别表示合成的两个输入线电压,Ui,i表示零线电压。同理定义Uj,j-,Uj,j+表示期望输出的两个极性相同的线电压。新型扇区划分下输出线电压合成的通用表达式如式(7)和式(8)所示。
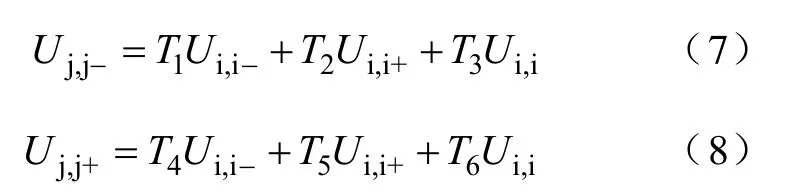
4 仿真与实验
为验证上文所提出的新型扇区划分模式的正确性,搭建了Matlab 仿真模型,其系统框图如图7 所示。输入相电压为 220V、100Hz,输出相电压为160V、50Hz,负载为20Ω、45mH 感性负载,呈星形联结方式。输入LC 滤波器为0.6mH,9.4μF,电感并联阻尼电阻为 50Ω,输出滤波器为 2.5mH、8.8μF,电容串联阻尼电阻为12Ω。
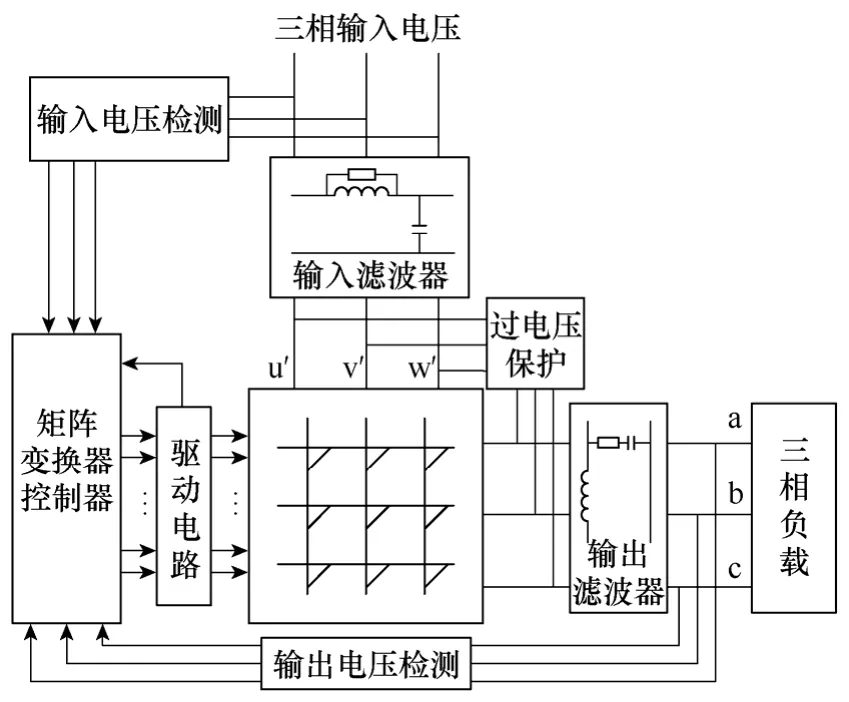
图7 矩阵变换器系统框图Fig.7 System Diagram of Matrix Converter
图8 所示为矩阵变换器新型扇区划分模式下的仿真波形。从上至下依次为输入电流、输入电压、输出电流和输出电压。输入、输出滤波器中加入阻尼电阻抑制LC 滤波器中存在的欠阻尼振荡。
从仿真波形可以看出,在新型扇区划分模式下很好地实现了矩阵变换器的控制。系统的谐波含量低,输入、输出都具有较高的正弦度。
在仿真研究的基础上制作了一台矩阵变换器的原理样机,该样机采用RB-IGBT(IXRP15N120)反向并联构成主功率电路的双向开关,以 DSP(TMS320F2812)与 CPLD(M4A5-192/96)为控制核心。DSP 用于计算占空比,CPLD 用于实现4 步换流与不同扇区组合下的占空比分配。
实验与仿真条件相同,实验时所有波形均是使用HIOKI8861~50 存储记录仪进行记录,波形的纵坐标均为实际的电压电流值。输入源采用CHROMA公司的AC source,实验平台照片如图9 所示。
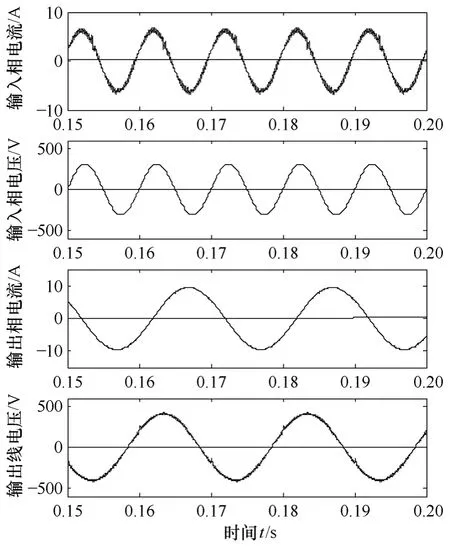
图8 新型扇区划分方式下矩阵变换器的仿真波形Fig.8 Simulation figure of matrix converter

图9 矩阵变换器实验平台Fig.9 Experimental bench of matrix converter
输入与输出的电压电流实验结果如图10 所示。图10a、10b 分别为输入和输出电流、电压波形。从实验波形可以看出在新型扇区划分方法下矩阵变换器具有较好的输入输出性能,系统主功率电路的效率为89.5%。
图11 所示为矩阵变换器的输入电流的频谱分析图,从上至下分别对应输入的电压与电流波形、输出的电压与电流波形。从波形可以看出基波成分占主导,谐波含量低,验证了本文所提出方法的有效性。
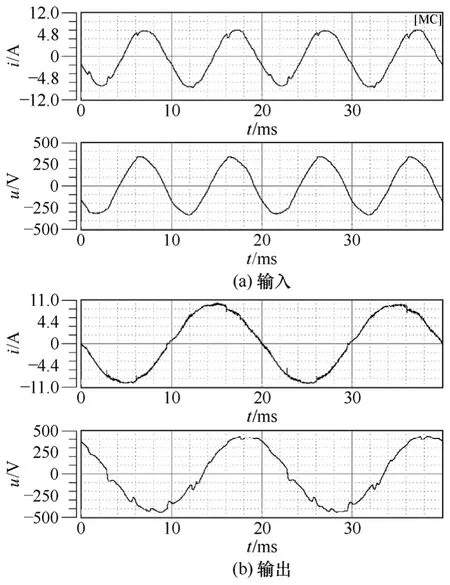
图10 新型扇区划分方式下矩阵变换器的实验波形Fig.10 Experimental waveforms of matrix converter
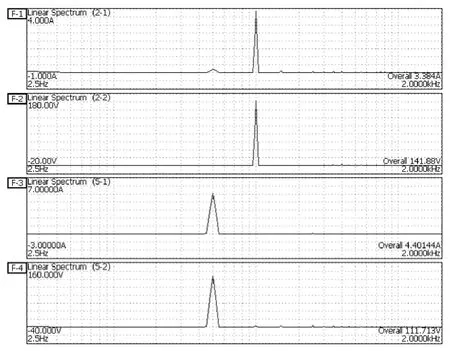
图11 输入输出波形的FFT 频谱图Fig.11 FFT analysis of input and output waveforms
为验证所提出的新型扇区划分方法在不平衡输入下的可行性,本文在三相输入电压的一相串入10Ω电阻模拟不平衡输入电压,实验波形如图11 所示。CH2-1、CH2-2、CH5-2 为矩阵变换器输入侧线电压的波形,CH5-1 为矩阵变换器的输出电压波形。从实验波形可以看出,在不平衡的输入电压下同样能够得到正弦度较高的输出电压波形(见图12)。
从实验结果可得出,本文所提出的新型扇区划分模式的正确性与可行性,该方法通过简单的逻辑判断将输出划分为3 个扇区,将扇区组合数由36个减少到18 个,简化了矩阵变换器的实现算法,同时也能够使矩阵变换器在不平衡的输入下得到了较好的输入输出性能。

图12 不平衡下的输入输出电压波形Fig.12 Experimental waveforms under unbalance supply
5 结论
(1)本文在双电压控制策略的基础上,通过分析扇区组合与占空比表达式之间的关系,提出了一种新型的输入输出扇区划分模式,并得出了对应扇区的输出电压合成表达式,降低了双电压调制策略算法的复杂程度。
(2)本文所提出的新型扇区划分方法能够在不平衡的输入下得到对称的三相输出电压,使其在双电压合成控制策略应用中具备通用性。
[1]Wheeler P W,Rodriguez J,Clare J C,et al.Matrix converters:a technology review[J].IEEE Transac-tions on Industrial Electronics,2002,49(2):276-288.
[2]孙凯,周大宁,梅杨.矩阵式变换器技术及其应用[M].北京:机械工业出版社,2007.
[3]Hidenori Hara,Eiji Yamamoto,Kang Junkoo,et al.Improvement of output voltage control performan-cefor low-speed operation of matrix converter[J].IEEE Transactions on Power Electronics,2005,20(6):1372-1378.
[4]Kai Sun,Daning Zhou,Lipei Huang,et al.A novel commutation method of matrix converter fed induction motor drive using RB-IGBT[J].IEEE Transactions on Industrial Applications,2007,43(3):777-786.
[5]梅杨,孙凯,黄立培.基于逆阻式 IGBT的三相/单相矩阵式变换器[J].电工技术学报,2007,22(3):91-95.Mei Yang,Sun Kai,Huang Lipei.Three-phase to single-phase matrix converter using RB-IGBT[J].Transactions of China Electrotechnical Society,2007,22(3):91-95.
[6]孙凯,梅杨,黄立培.矩阵式变换器驱动异步电机调速系统的非线性自抗扰控制[J].电工技术学报,2007,22(12):39-45.Sun Kai,Mei Yang,Huang Lipei.A nonlinear auto-disturbance rejection control for matrix converter fed induction motor drive system[J].Transactions of China Electrotechnical Society,2007,22(12):39-45.
[7]权建洲,吴保芳,孙容磊,等.基于前馈补偿的SPWM 矩阵变换器控制策略研究[J].中国电机工程学报,2006,26(5):88-94.Quan Jianzhou,Wu Baofang,Sun Ronglei,et al.A compensation method for SPWM matrix converter based on feed-forward control[J].Proceedings of the CSEE,2006,26(5):88-94.
[8]何必,张晓锋,林桦,等.采用零矢量补偿的矩阵变换器电流控制策略[J].中国电机工程学报,2007,27(13):53-57.He Bi,Zhang Xiaofeng,Lin Hua,et al.Current control strategies for matrix converter using zero vectors[J].Proceedings of the CSEE,2007,27(13):53-57.
[9]Ishiguro A,Furuhashi T,Okuma S.A novel control method for forced commutated cycloconverters using instantaneous values of input line-to-line voltages[J].IEEE Transactions on Industrial Electronics,1991,38(3):166-172.
[10]Junichi Itoh,Ikuya Sato,Akihiro Odaka,et al.A novel approach to practical matrix converter motor drive system with reverse blocking IGBT[J].IEEE Transactions on Power Electronics,2005,20(6):1356-1363.
[11]陈希有,丛树久,陈学允.双电压合成矩阵变换器特性与电压扇区的关系分析[J].中国电机工程学报,2001,21(9):63-67.Chen Xiyou,Cong Shujiu,Chen Xueyun.The analysis of the relationship between the voltage sectors and performances of matrix converter based on two-voltage synthesis[J].Proceedings of the CSEE,2001,21(9):63-67.
[12]郭有贵.矩阵变换器双电压合成定理及其自动调节能力研究[J].中国电机工程学报,2006,26(21):71-75.Guo Yougui.Research on double input line-to-line voltages composition theorem and its self-adjustability[J].Proceedings of the CSEE,2006,26(21):71-75.
[13]王毅,陈希有,徐殿国.双电压合成矩阵变换器闭环控制的研究[J].中国电机工程学报,2002,22(1):74-79.Wang Yi,Chen Xiyou,Xu Dianguo.The research on closed-loop control method for matrix converter based on double line-to-line voltage synthesis[J].Proceedings of the CSEE,2002,22(1):74-79.
[14]仇红奎,周波,史明明.矩阵变换器双电压简化控制策略[J].中国电机工程学报,2008,28(36):23-27.Qiu Hongkui,Zhou Bo,Shi Mingming.Simplified control strategy of input line-to-line voltages for matrix converter[J].Proceedings of the CSEE,2008,28(36):23-27.
[15]马星河,谭国俊,汪旭冬,等.一种改进的矩阵变换器双电压合成控制策略[J].电工技术学报,2009,24(4):126-132,138.Ma Xinghe,Tan Guojun,Wang Xudong,et al.An improved two line voltage synthesis control strategy of matrix converter[J].Transactions of China Electro-technical Society,2009,24(4):126-132 ,138.

