基于自抗扰控制的开关磁阻电机转速闭环性能

昝小舒 陈 昊

（1.中国矿业大学电力工程学院 徐州 221116 2.中国矿业大学信电学院 徐州 221116）

1 引言

集成起动/发电系统（Integrated Starter and Generator，ISG）是混合动力汽车采用的一种驱动方式，它将起动机和发电机用一种电机来代替，减少了车辆的体积、重量和维护，增加了系统的可靠性，并且通过低速和高速的助力，提高了燃油效率、降低了尾气排放[1,2]。开关磁阻起动/发电系统由于起动转矩大、速度范围宽、发电效率高，是近年来的研究热点[3]。20世纪80年代，美国GE公司成功研制出功率达250 kW的开关磁阻ISG系统[4]。国内也于21世纪初开始了开关磁阻 ISG 系统的研究，南京航天航空大学研制出了6kW样机[5,6]，西北工业大学也进行了理论和样机研究[7]。近几年来，江苏大学对开关磁阻ISG在车辆上的应用进行了较多尝试[8,9]。

助力是ISG 系统的一种重要功能，主要分为两种情况：一是在市区，车况复杂，红绿灯多，起停频繁的情况下，发动机没有点火，车辆在怠速以下，全靠ISG 系统带动车辆低速运行；二是在上坡或者负载较重的情况下，在发动机正常运行的同时，ISG系统进行助力。车辆要求ISG 助力控制系统转速响应快、抗干扰能力强、稳定性能好。开关磁阻电机由于其特殊的双凸极结构和脉冲电流供电方式，是一个严重非线性的系统[10]，采用传统PID 控制为代表的线性控制方法不能满足其较高的动静态特性要求。自抗扰控制是20 世纪90年代由韩京清研究员提出来的一种新型控制方法[11]，它把控制系统参数的变化看成系统的内部和外部扰动的总和，并进行观测补偿。自抗扰控制能够实现快速、无超调响应，具有非常强的鲁棒性，能够解决传统PID 控制器的快速性与超调性之间的矛盾。本文以开关磁阻ISG助力系统为研究背景，对基于自抗扰控制的开关磁阻电机转速闭环性能进行了研究。

2 基于ISG 助力系统的开关磁阻电机转速闭环控制系统

本文研究的开关磁阻电机转速闭环系统是基于开关磁阻ISG助力控制系统的。该系统主要由发动机、开关磁阻电机、负载、功率变换器、控制器、电流检测、电压检测、位置检测、电池等组成，如图1所示。开关磁阻电机首先由蓄电池供电电动运行，带动发动机转动到怠速以上，发动机点火起动；然后开关磁阻电机由发动机带动进入发电运行，为用电设备供电和电池充电；如果电池允许，在怠速以下或者正常运行时，可以进行助力；在车辆制动或减速时，可以实现发电制动，回收能量。开关磁阻ISG系统可以实现发动机怠速以上起动，并且在低速时可以进行助力控制，可以避免燃油发动机低速不完全燃烧的尾气排放，提高车辆的动力性能，提高燃油利用率。

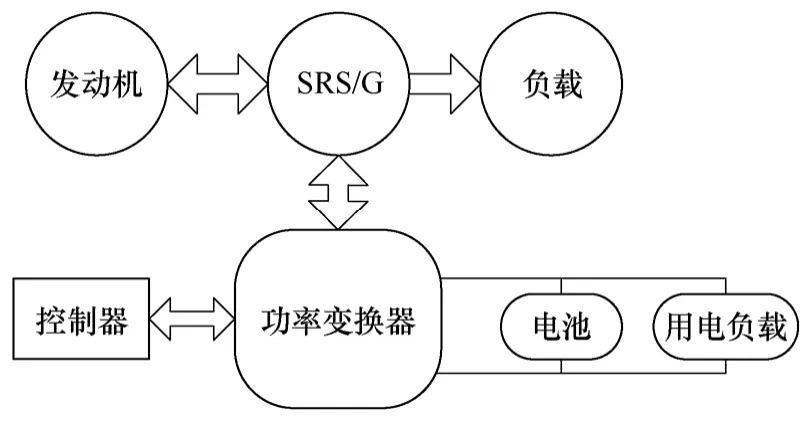
图1 开关磁阻ISG 系统Fig.1 Reluctance switched ISG system

3 基于自抗扰控制转速闭环系统设计

3.1 自抗扰控制的基本原理

传统的PID 控制采用对控制对象的输出误差进行削减控制，可以忽略控制对象的数学模型，实现简单，在调速、运动等控制领域得到广泛的应用。但是 PID 控制是基于线性控制系统的一种控制策略，对于控制系统的不同状态需要调整控制参数。而非线性系统是一个参数和结构时变的系统，单一状态的PID 参数很难在整个控制范围内得到理想的控制效果。自抗扰控制是在吸取了传统的PID 控制的优点，并且克服了PID 控制缺点的基础上提出来的一种新型控制策略[12]。它对控制系统的外部和内部扰动进行补偿，不依赖于被控对象的精确数学模型，使系统线性化为积分串联型结构，便于控制。

文献[12]的自抗扰控制原理如图2 所示，它由非线性跟踪微分器(TD)[13]、非线性误差反馈控制律(NLSEF)[14]和扩张状态观测器(ESO)[15]三部分组成。非线性跟踪微分器(TD)可以避免经典PID 控制中因给定的突变而造成的控制量的变化过大，最终输出量有较大超调的缺点。扩张状态观测器(ESO)是自抗扰控制器的核心控制部分，它以控制对象的输入和输出量作为判断依据，估算出模型的误差变化以及外部扰动，并且将这些扰动变成补偿加入到反馈中，从而稳定控制效果。非线性状态误差反馈控制律(NLSEF)能使误差以指数形式呈数量级减小，由于只用比例和微分环节设计控制器，避免了传统PID 控制中积分的副作用。

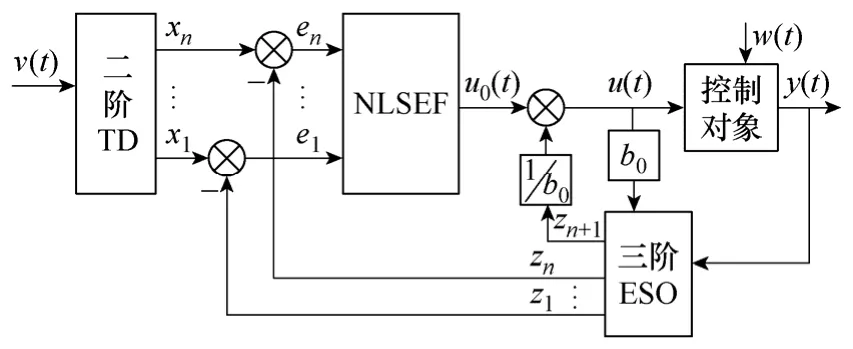
图2 自抗扰控制原理图Fig.2 Auto disturbance rejection control schematic

3.2 开关磁阻电机的数学模型

根据文献[7]，开关磁阻电机电压平衡方程为

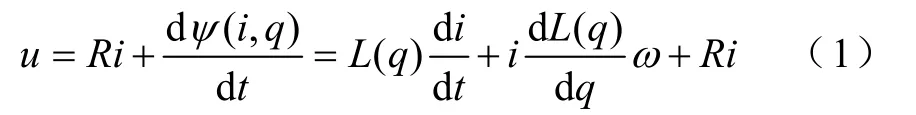
式中u—绕组电压；

R—绕组电阻；

i—绕组电流；

ψ—绕组磁链；

L—绕组电感；

ω—电机转速。

电磁转矩方程为

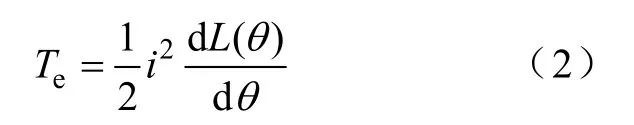
机电联系方程为

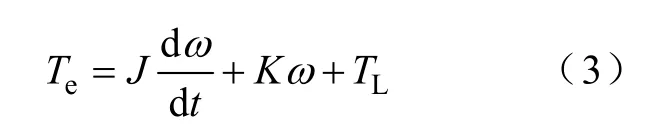
式中J—转动惯量；

K—阻尼系数；TL—负载转矩。

式（1）～式（3）构成了开关磁阻电机的数学模型。

3.3 基于自抗扰控制的开关磁阻电机转速闭环设计

以开关磁阻ISG 助力控制系统为控制对象，本文取电机转速为控制量来进行自抗扰控制器的设计，由式（3）可以得出

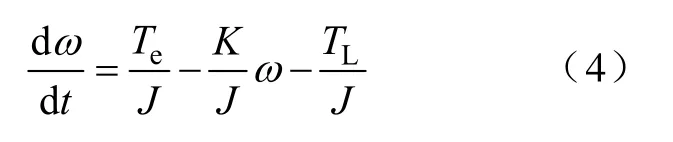
式（4）可以进一步变成

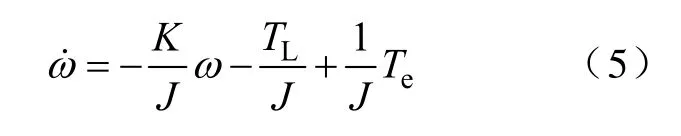
因此，开关磁阻电机转速闭环控制系统可以表示为

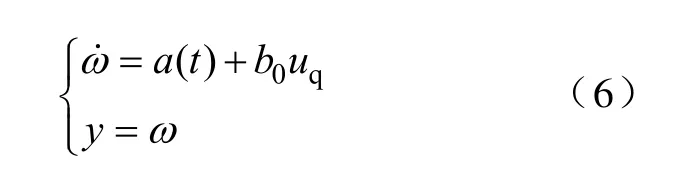
如果a(t)能够被自抗扰控制器精确的反馈，则开关磁阻电机转速闭环控制系统则可以转换成一个一阶系统控制问题。

开关磁阻ISG 助力系统中，随着车辆运行状况的不一样，电机的转速给定是多变的，自抗扰控制器的TD 模块可以让控制器的给定更加迅速的逼近实际要求的转速，并且过滤掉噪声的影响。

取电机的给定转速ω*为输入，通过TD 滤波器可以得到适当的过度过程ω1，TD 滤波器离散化后为

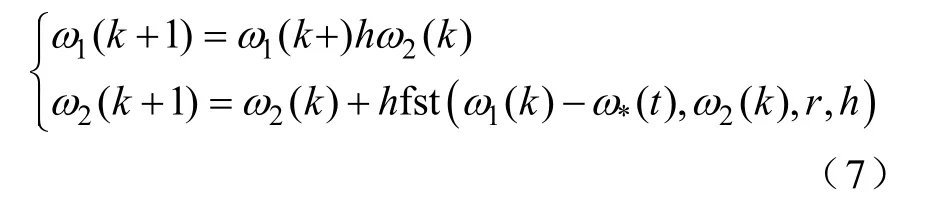
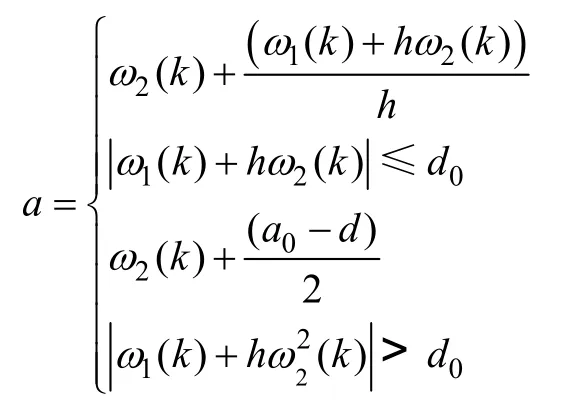
r为跟踪速度参数，r越大，输出ω1越接近给定ω*，跟踪越好；h为积分步长，h越大，滤波效果越好；fst 为离散时间系统最优控制函数。

为了简化控制结构，本文采用一个二阶的ESO和一个一阶的NLSEF 来进行开关磁阻电机转速闭环控制系统的设计，如图3 所示。

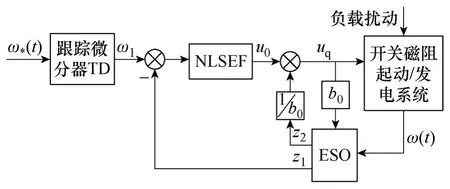
图3 基于自抗扰开关磁阻起动/发电系统控制Fig.3 Reluctance switched ISG system by auto disturbance rejection control

二阶ESO 根据系统的测量转速ω(t)和系统的输出量u(t)来估测系统总扰动的实时作用量a(t)。ESO离散方程为

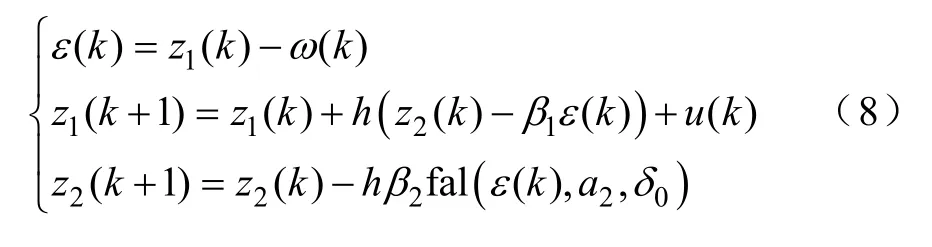
式中，β1，β2，δ0都是可调参数；fal()为非线性函数，且

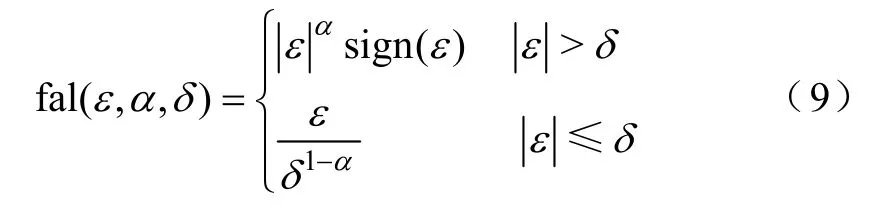
一阶离散NLSEF 为

最终的输出控制量为

式中，u0为非线性反馈；u0=β0fal（-y1（t），α0,δ0）；-z2/b0为内部和外部的扰动的补偿。

当ESO 最终收敛时，第二个输出z2就可以跟踪包含了内部和外部的扰动a(t)，实现了开关磁阻电机转速闭环控制中内部和外部的扰动的补偿。

实际控制中，为了控制方便，取自抗扰控制器的最终输出为电压PWM 占空比。通过调节PWM占空比的大小最终控制电机的转速。

4 仿真研究

4.1 仿真模型

仿真研究可以完成实际系统中难以实现、工作量大或者危险的工作，为实际电机的设计提供可靠的依据。本文采用Matlab 仿真软件对开关磁阻ISG系统进行了仿真建模，利用仿真模型对开关磁阻转速闭合系统的自抗扰控制性能和参数进行估算。仿真模型中开关磁阻电机功率为 500W，额定转速504r/min，供电电压24V 定子相绕组电阻R=0.45Ω，系统转动惯量J=0.001kg·m2，电机系统粘滞系数ζ=4μN·s/rad。仿真模型中包括开关磁阻电机模型、自抗扰控制模块、PWM 控制模块、机电转化模块等。

4.2 助力自抗扰控制仿真结果

为了验证自抗扰控制在开关磁阻ISG 助力系统转速闭环控制中的效果，分别对外部扰动中系统的起动，突加、突卸负载情况，转速跟随情况和内部定子绕组电阻的变化情况进行了仿真实验。并对相同情况下PID 控制的起动、突加、突卸负载情况进行了各方面的仿真结果比较。

4.2.1 起动情况仿真

图4 和图5 分别是400r/min 和600r/min 转速下，系统带负载1N·m 起动的转速、电流和转矩变化曲线。由仿真曲线可以看出：转速起动平稳而且起动时间短，目标转速400r/min 下起动时间0.28s，目标转速600r/min 下起动时间0.41s，满足助力控制起动速度快的要求；两种目标速度下，起动时基本无超调，稳定时间短；起动完成，稳定情况下转速波动小，目标转速400r/min 下转速波动为2%左右，600r/min 下转速波动为3%左右。因此在自抗扰控制下，助力控制系统能够及时起动并且迅速地稳定运行。

4.2.2 突加突卸负载仿真

自抗扰控制最重要的能力是对负载扰动的快速调节。图6 和图7 所示分别是400r/min 和600r/min转速下，系统突加突卸1N·m 负载起动的转速、电流和转矩变化曲线。由图可以看出：平稳状态下突加突卸负载，转矩、转速恢复平稳速度快；目标转速400r/min 下突加负载恢复时间0.09s，目标转速600r/min 下突加负载恢复时间 0.14s；目标转速400r/min 下突卸负载恢复时间 0.11s，目标转速600r/min 下突卸负载恢复时间0.16s。自抗扰控制对于负载扰动下转速恢复时间快、转矩稳定时间短，能够满足助力控制下，车辆负载多变的状态。

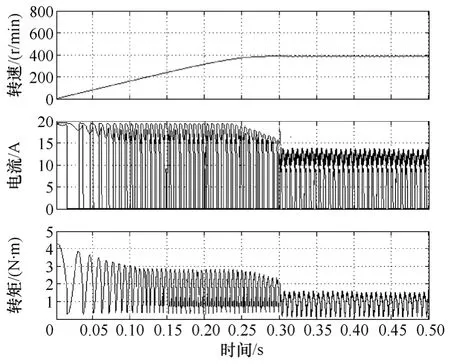
图4 自抗扰控制400r/min 起动Fig.4 Starting of 400r/min by auto disturbance rejection control

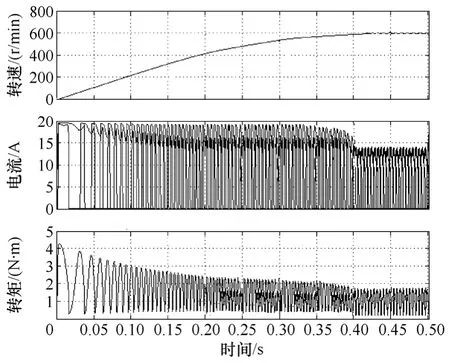
图5 自抗扰控制600r/min 起动Fig.5 Starting of 600 r/min by auto disturbance rejection control

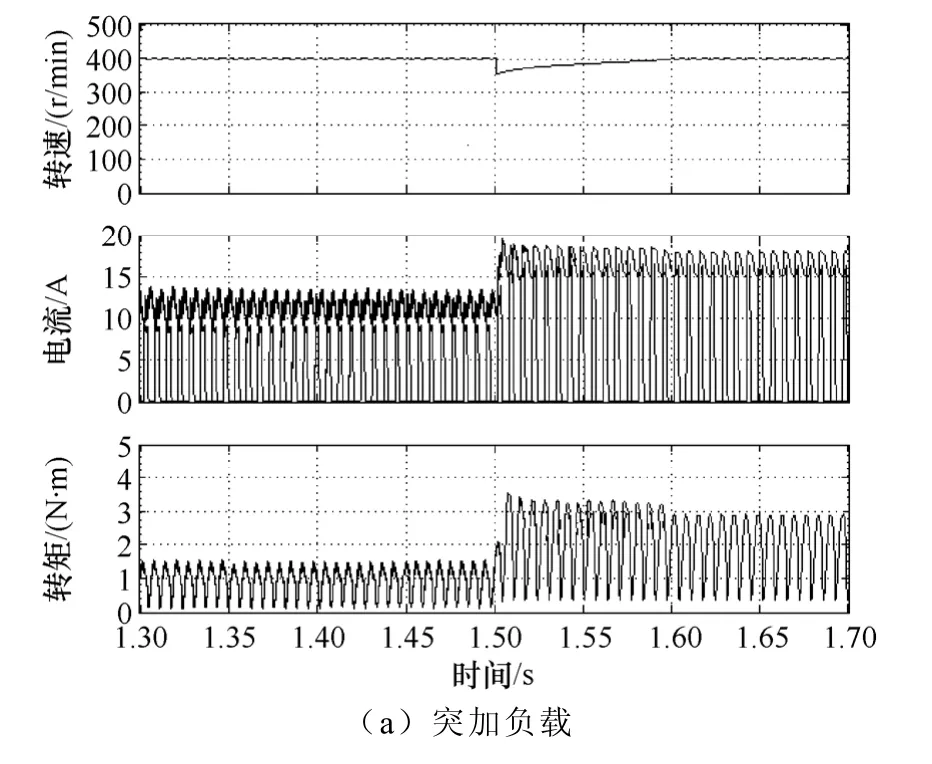
图6 转速400r/min 抗干扰转速波形Fig.6 Anti-disturbance speed waveform of 400r/min

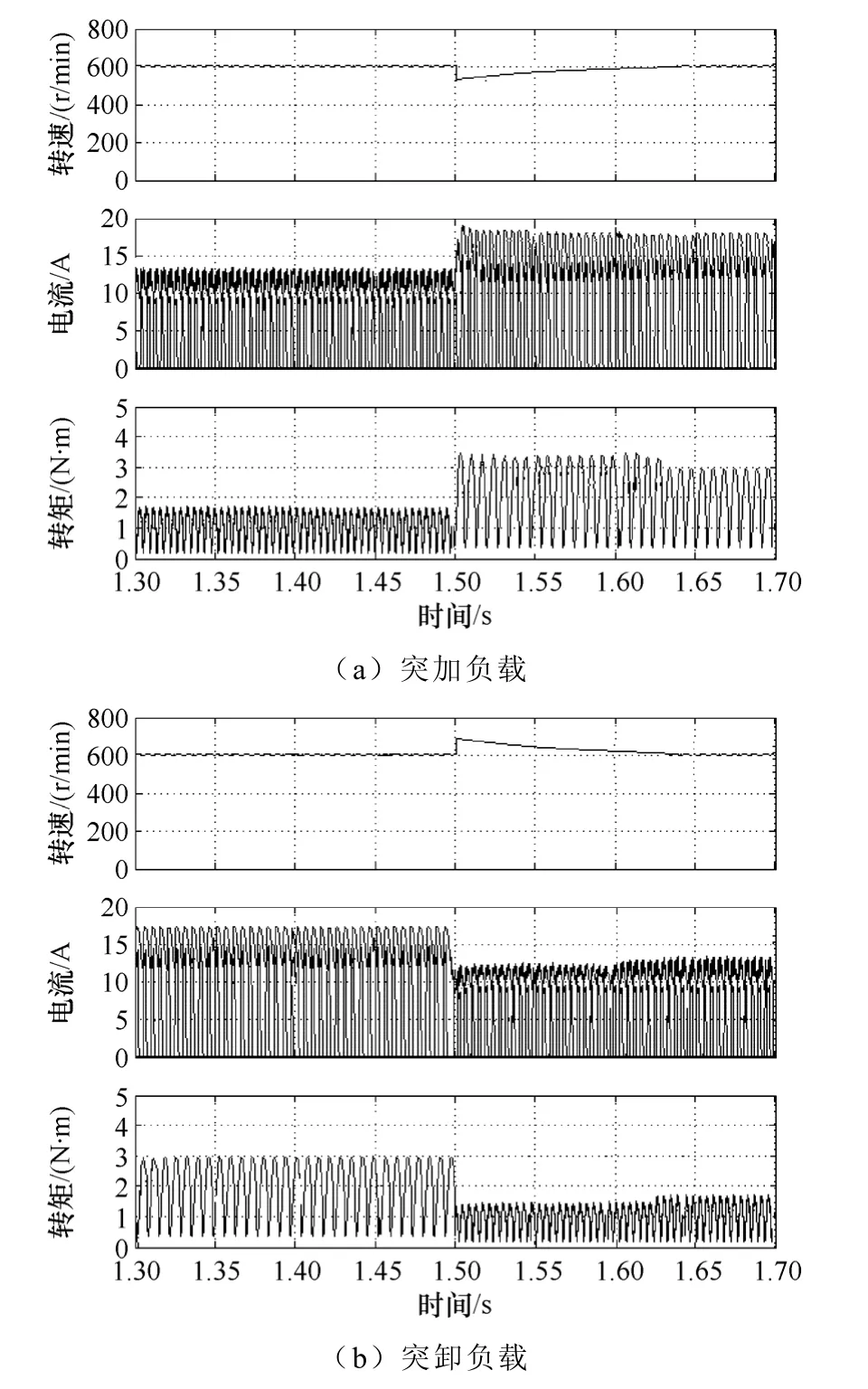
图7 转速600r/min 抗干扰转速波形Fig.7 Anti-disturbance speed waveform of 600r/min

4.2.3 转速跟随性仿真

开关磁阻ISG 助力控制系统中，电机的给定转速随着车辆的路况是实时变化的，因此控制器的跟随性尤其重要。为了测试自抗扰控制转速的跟随性能，分别对转速从200r/min 到1 000r/min 突加两次400r/min 转速，转速从1 000r/min 升到200r/min 突减两次400r/min 转速的情况进行了仿真，如图8 所示。由仿真结果可以知道：突加400r/min的转速，转速可以在0.3s 左右的时候稳定到新的转速，基本无超调；突卸400r/min的转速，转速可以在0.4s 左右的时候稳定到新的转速，基本无超调。基于自抗扰控制的开关磁阻电机转速跟随性能较好。

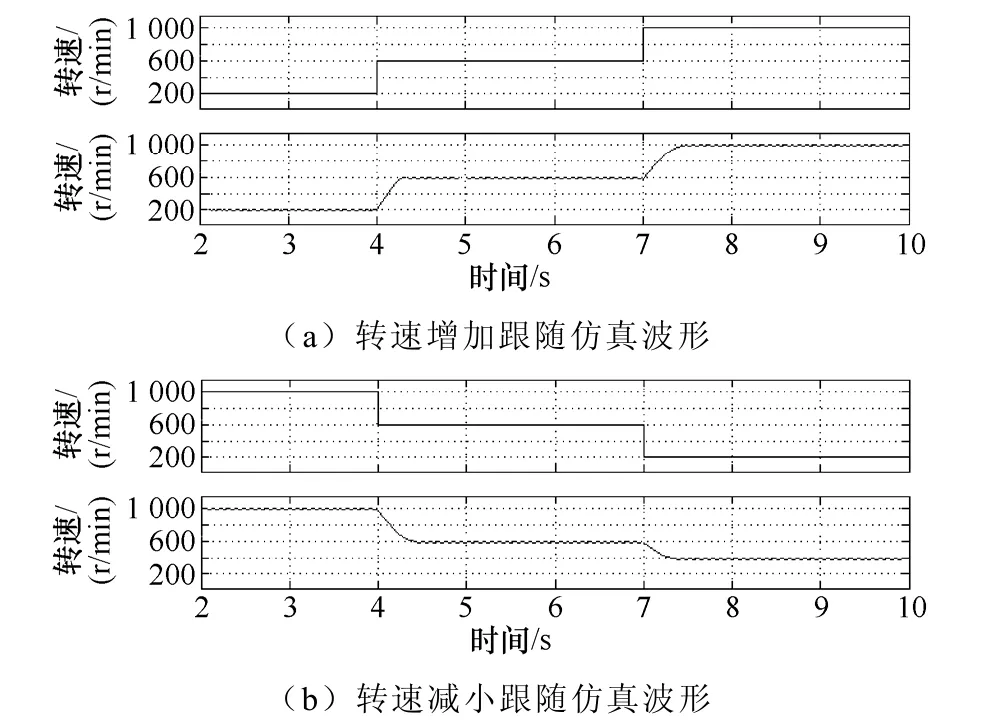
图8 转速跟随性能波形Fig.8 Rotating speed tracking waveform

4.2.4 模型内部参数变化影响仿真

开关磁阻电机由于结构特点，难以获得精确的电机数学模型；而且随着运行状态的不同，模型始终处于变化之中。随着温度的变化，定子绕组的电阻会有一定的变化，如图9 所示设定定子绕组电阻R=0.55Ω下的起动情况，图10 为在1.5s 时候定子电阻由0.45Ω变化为0.55Ω的系统稳态情况。由仿真结果可知：温度变化引起的定子绕组电阻变化对系统的起动、稳定基本没有影响，自抗扰控制对于模型参数的变化带来的内部扰动有着很好的抵抗能力。

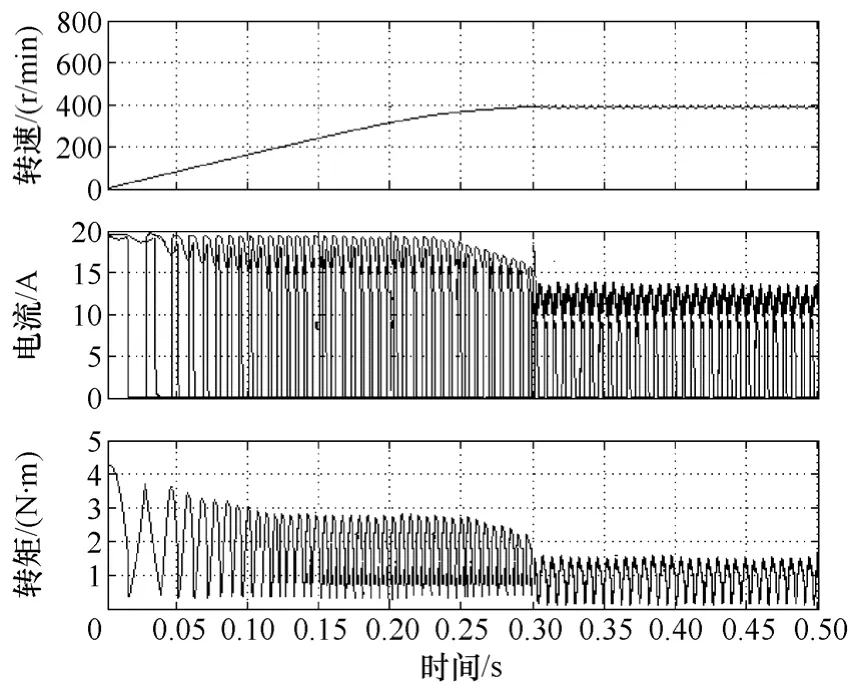
图9 温度变化下自抗扰控制400r/min 起动情况Fig.9 Starting of 400r/min by auto disturbance rejection control at temperature change

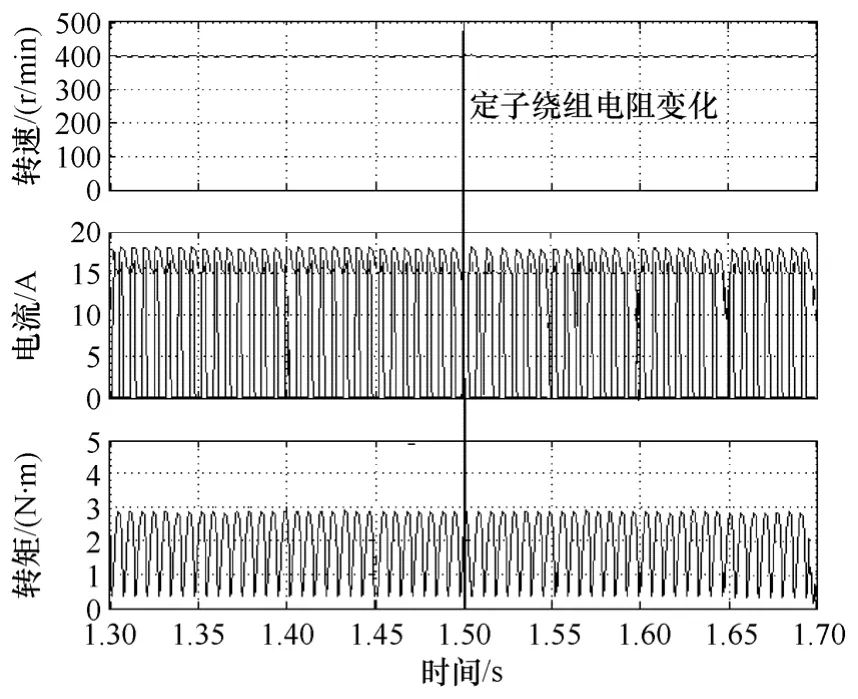
图10 温度变化下自抗扰控制400 r/min 稳态情况Fig.10 Steady state of 400r/min by auto disturbance rejection control at temperature change

4.2.5 自抗扰控制与PID 控制性能比较

为了对比自抗扰控制的控制效果，对同样负载条件下的PID 控制的助力控制系统进行了仿真。为了方便对比，仿真分两种情况：调节PID 参数，使得两种控制方法下的起动时间相同，见表1；调节PID 参数，使得两种控制方法下的起动超调为零，见表2。同时对两种情况下的突加突卸负载情况进行了仿真对比。

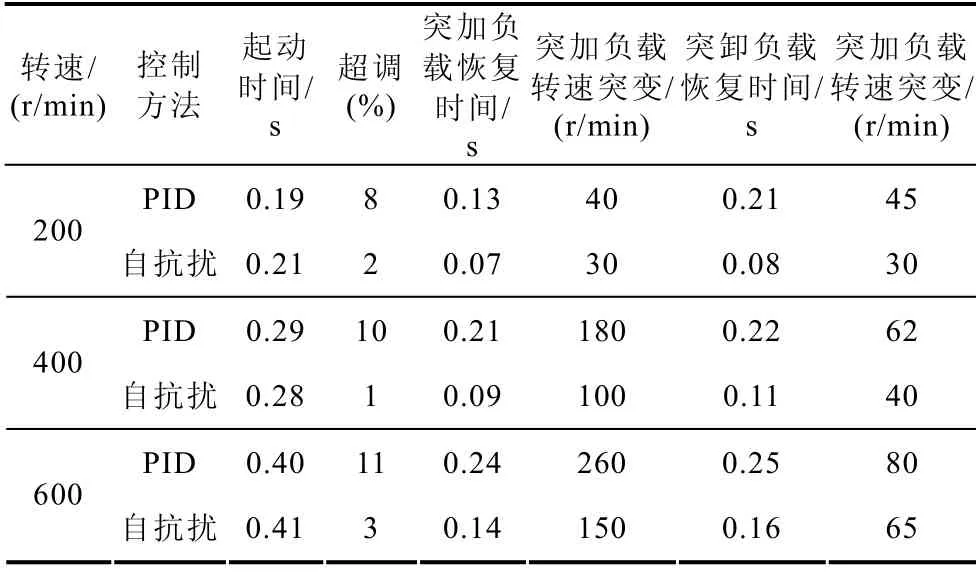
表1 仿真结果比较1Tab.1 Comparison of simulation 1

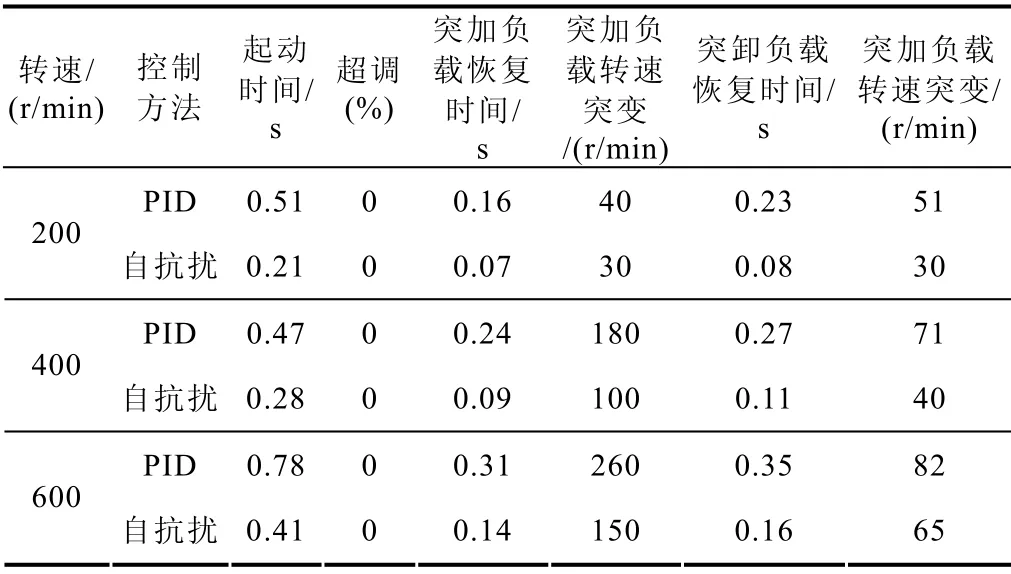
表2 仿真结果比较2Tab.2 Comparison of simulation 2

由表1 可以看出：基本相同的起动时间下，自抗扰控制下的起动超调很小，同时在突加和突卸负载的时候，自抗扰控制下的转速恢复时间短、转速变化小。由表2 可以看出：基本无超调情况下，自抗扰控制下起动时间比PID 控制下的更短，同时在突加和突卸负载的时候，自抗扰控制下的转速恢复时间短、转速变化小。因此，自抗扰控制下的开关磁阻助力控制系统，在起动性能、抗负载扰动能力都比传统的PID 控制有提高。

5 实验结果

5.1 实验平台

为了进一步评价新控制方法的有效性，对基于自抗扰控制的开关磁阻电机转速闭合系统进行了样机实验。实验平台如图11 所示，该平台包括：一台三相12/8 结构、额定功率500W、额定转速500r/mn的开关磁阻电机、负载（由一台四相8/6 结构、额定功率3kW、额定转速1 000r/min的开关磁阻电机模拟）、功率变换器、微机控制器、电池组、负载设备、转速转矩仪、上位机控制处理系统等。该实验平台可以模拟开关磁阻ISG 系统的起动、发电、助力等多种运行状态，可对新型控制策略进行实际的样机验证。

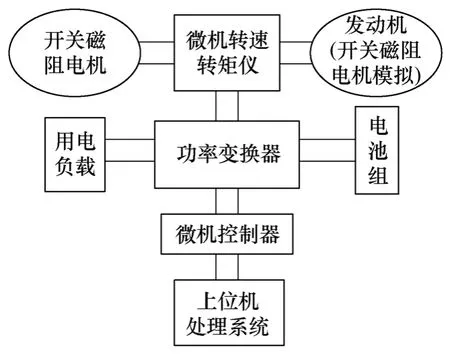
图11 开关磁阻ISG 系统实验平台Fig.11 Switched reluctance ISG experimental platform

5.2 实验结果

为了多方面验证自抗扰控制方法在开关磁阻ISG 助力转速闭环系统中的效果，采用图11 所示的实验开关磁阻ISG 系统样机平台进行了多项动静态转速性能的实验，实验内容包括：不同转速下的起动情况，平稳运行时的负载扰动情况、给定转速变化时的转速跟踪情况。

5.2.1 起动实验结果

采用自抗扰控制方法，开关磁阻ISG 助力系统样机起动实验波形如图12 和图13 所示。由实验波形可以看出：两种转速下，电机均能快速无超调起动，给定转速400r/min 下起动时间为0.3s，给定转速600r/min 下起动时间为0.8s。因此，本系统起动迅速，达到目标转速后能够迅速平稳运行，可以满足一般车辆电动助力运行的需要。

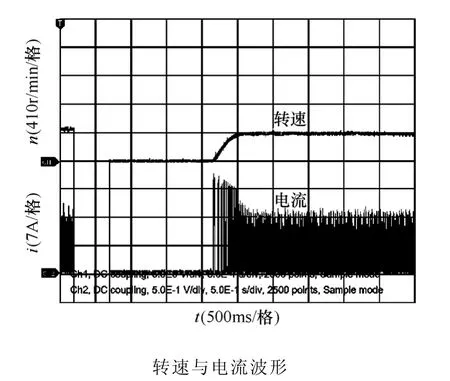
图12 转速400r/min 起动与稳定波形Fig.12 Starting and stability waveform of 400r/min

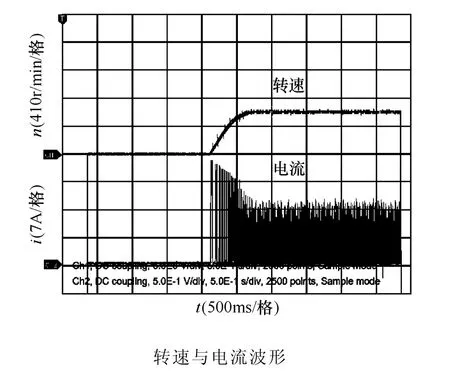
图13 转速600r/min 起动与稳定波形Fig.13 Starting and stability waveform of 600r/min

5.2.2 抗干扰实验结果

采用自抗扰控制方法，开关磁阻ISG 助力系统的稳态抗干扰实验波形如图14 和图15 所示。分别为转速400r/min 和600r/min 时突加和突卸1N·m负载时的转速电流波动情况。由图可以看出：突加突卸负载，转速都能够在0.3s的时间内恢复到平稳状态，转速波动在50r/min 左右，转速波动时间短、转速波动小恢复迅速。采用自抗扰方法，开关磁阻ISG 助力系统的转速抗干扰性能突出、鲁棒性好。

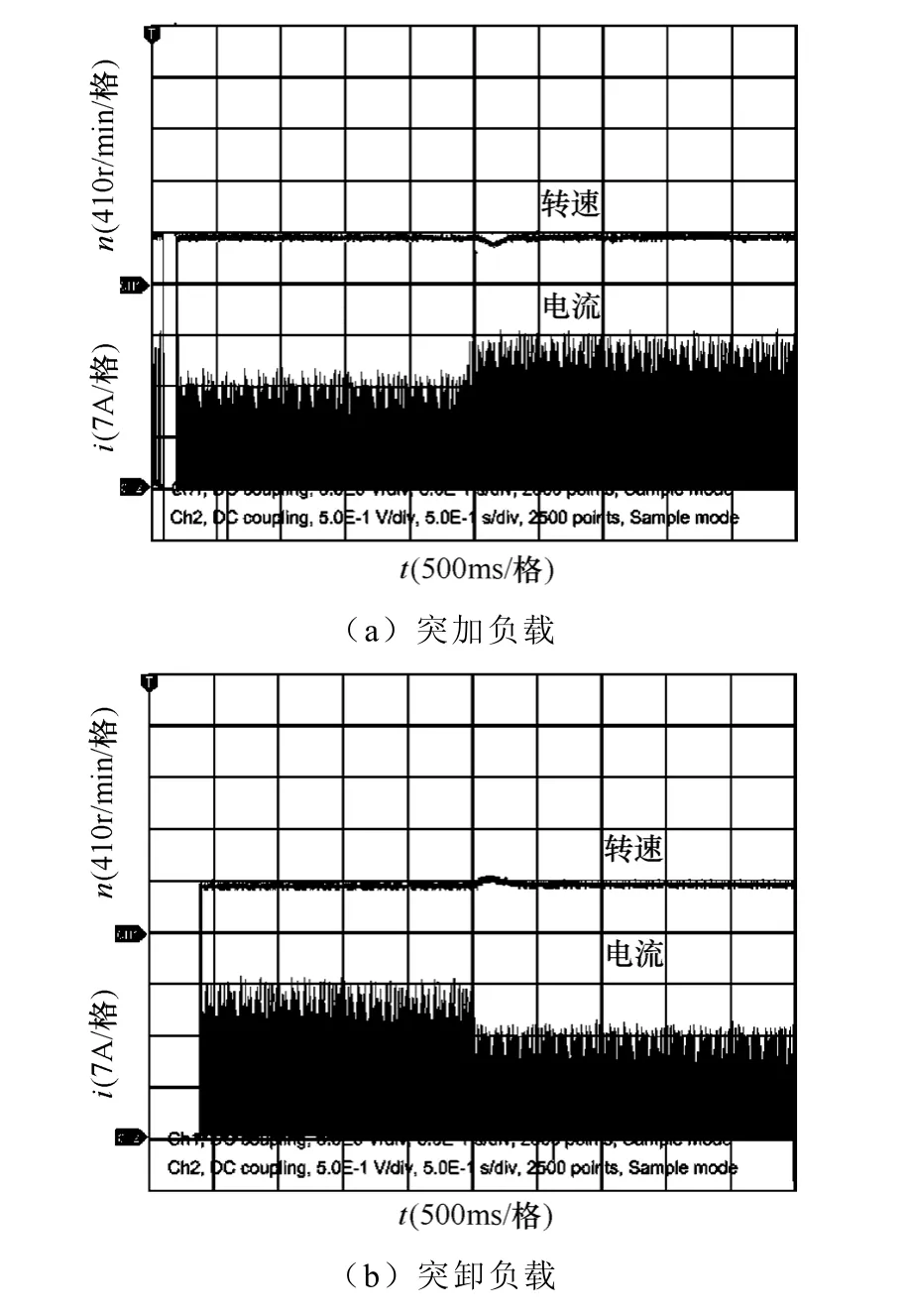
图14 转速400r/min 抗干扰转速波形Fig.14 Anti-disturbance speed waveform of 400r/min

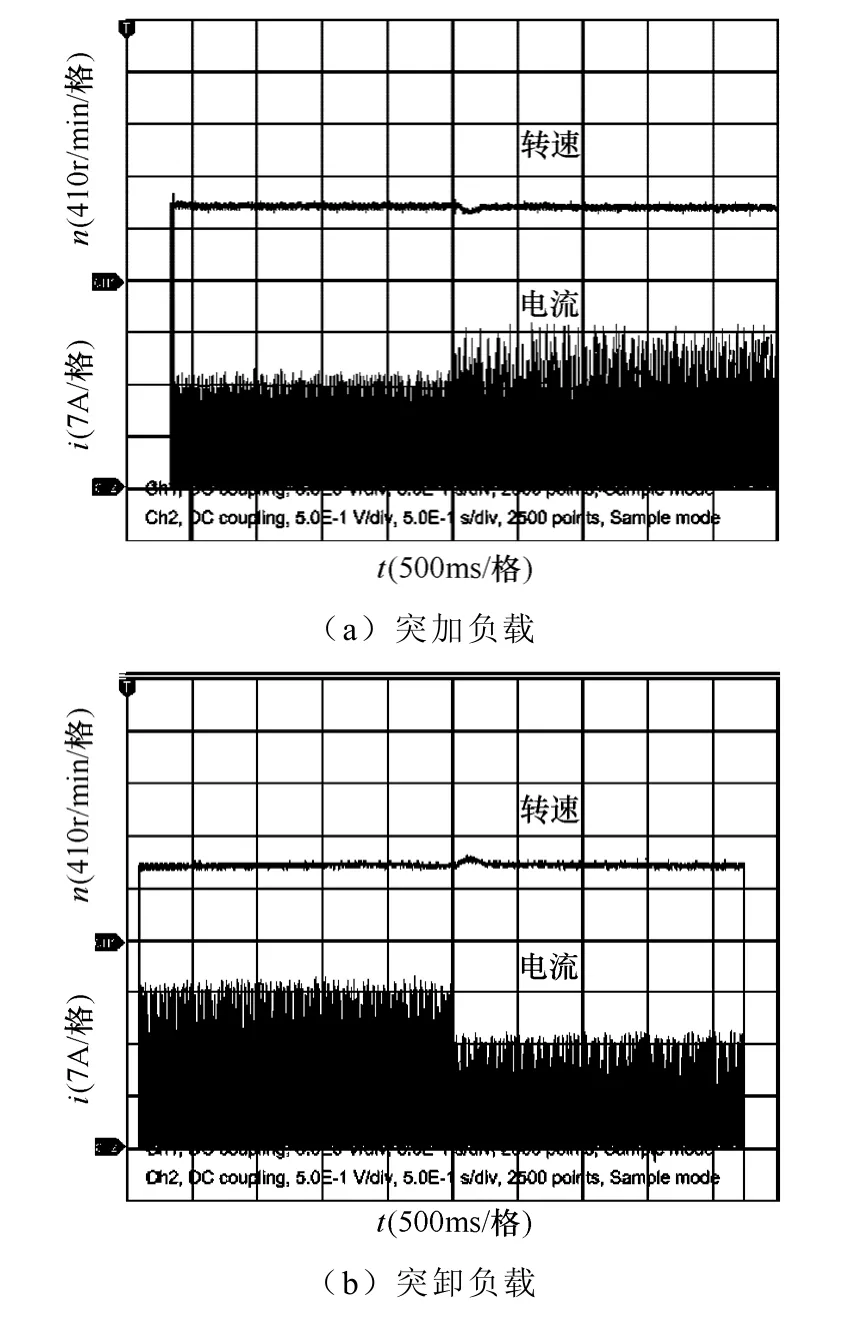
图15 转速600r/min 抗干扰转速波形Fig.15 Anti-disturbance speed waveform of 600r/min

5.2.3 跟随性实验结果

车辆在运行时，转速随着路况是不断变化的，开关磁阻ISG 助力系统必须能够迅速的跟随给定目标转速变化。图16 和图17 分别是加速转速跟随和减速转速跟随实验波形。

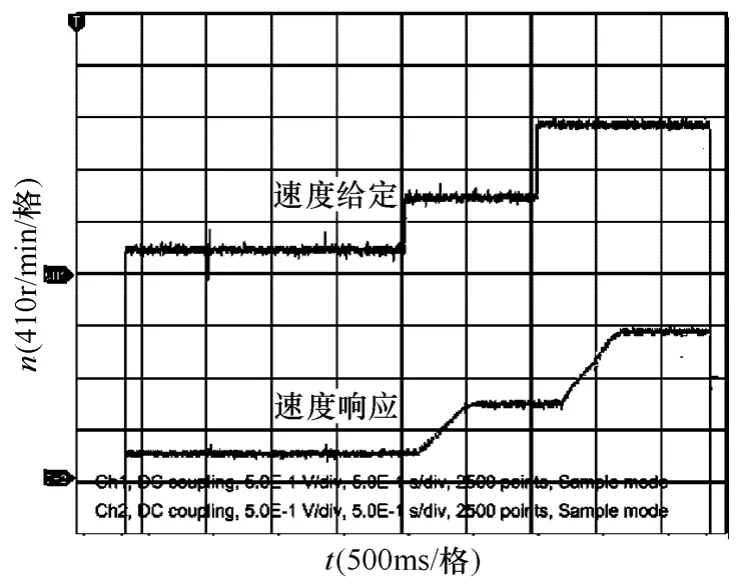
图16 加速转速跟踪实验波形Fig.16 Rotating speed tracking waveform of acceleration

图17 减速转速跟踪实验波形Fig.17 Rotating speed tracking waveform of deceleration

由图可以看出：给定转速变化时，电机反应延时0.2s 左右，这和控制器以及机械延时有关，而仿真并没有这个延时；在突加400r/min 转速下，转速跟踪可以在0.4s 左右完成；突减400r/min 转速下，转速跟踪可以在0.5s 左右完成，基本可以满足车辆的快速响应的要求。跟随实验和仿真实验相比，过渡时间稍长，这和实际的控制系统和仿真的差别造成的，基本上仿真和实验比较一致。

6 结论

本文根据自抗扰控制器的基本原理，完成了开关磁阻电机转速闭环控制器的设计。利用自抗扰控制方法的特性避开了开关磁阻电机数学模型的不精确性。然后利用仿真模型对自抗扰控制器的控制性能在外部负载扰动和内部参数变化的情况进行了仿真实验，并与PID 控制进行了比较。最后利用开关磁阻ISG 系统实验平台，对自抗扰控制器在转速闭环控制中的的实际运行性能进行了验证。仿真和实验结果都表明：这种新的控制方法具有优良的动静态性能，利用内部状态观测器对外部的负载扰动和内部的参数变化都能够进行提前的观测和补偿，具有良好的鲁棒性能。自抗扰控制方法对于开关磁阻ISG 助力系统这样一个给定多变、严重非线性、扰动多、参数变化大的控制对象具有较好的应用前景和现实意义。

[1]周大森,吴斌,张博彦,等.辅助混合动力电动汽车技术的研究[J].北京工业大学学报,2004,30(2):207-209.Zhou Dasen,Wu Bin,Zhang Boyan,et al.Study on the technology of auxiliary hybrid electric vehicle[J].Journal of Beijing University of Technology,2004,30(2):207-209.

[2]Elbuluk M E,Kankan M D.Potential starter/ generator technologies for future aerospace applications[J].IEEE AES Systems,1997,21(5):24-31.

[3]Miller J M.Starter-alternator for hybrid electric vehicle:comparison of induction and variable reluctance machines and drives[C].IEEE IAS Annual Meeting,1998(1):513-523.

[4]Ferreira C A,Richter E.Detailed design of a switched reluctance 250kW starter/generator for an aircraft engine[J].Proc.SAE Trans on Aerospace,1993,102(1):289-300.

[5]刘闯.开关磁阻电机起动/发电系统理论研究与工程实践[D].南京:南京航空航天大学,2000.

[6]刘闯,朱学忠,等.6kW 开关磁阻起动/发电系统设计及实现[J].南京航空航天大学学报,2000,32(3):245-250.Liu Chuang,Zhu Xuezhong,et al.Design and research of 6kW switched reluctance starter/generator system[J].Journal of Nanjing University of Aeron-autics & Astronautics,2000,32(3):245-250.

[7]李声晋.开关磁阻起动/发电系统研究与实践[D].西安:西安交通大学,2000.

[8]茅靖峰,赵德安,等.混合动力汽车用开关磁阻起动/发电机控制系统设计[J].微电机,2006,39(1):82-85.Mao Jingfeng,Zhao De’an,et al.Control system of switched reluctance starter/generator used in hybrid electric vehicle[J].Micromotor,2006,39(1):82-85.

[9]乔建光,赵德安,等.开关磁阻起动/发电机控制器的硬件实现[J].电工技术杂志,2004,1(12):39-41 Qiao Jianguang,Zhao Dean,et al.The hardware realization of controller on switched reluctance starter and generator[J].Electrotechnical Journal,2004,1(12):39-41.

[10]王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,2002.

[11]韩京清.从PID 技术到自抗扰控制技术[J].控制工程,2002,9(3):13-18.Han Jingqing.From PID technique to active disturbances rejection control technique[J].Control Engineering of China,2002,9(3):13-18.

[12]韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.Han Jingqing.Active disturbance rejection controller and its applications[J].Control and Decision,1998,13(1):19-23.

[13]韩京清,王伟.跟踪微分器[J].系统科学与数学,1994,14(2):177-183.Han Jingqin.Wang Wei.Nonlinear tracking-differen-tiator[J].Syst Sci Math Scis,1994,14(2):177-183.

[14]Liu Xizhe,Wu Jie,Lei Chunlin.Speed distinguish and control of PMSLM using expand state observer[J].Intelligent Control and Automation,2004,5(1):4568-4572.

[15]韩京清.非线性状态误差反馈控制律—NLSEF[J].控制与决策,1995,11(3):221-225.Han Jingqing.Nonlinear states errors feedback control-NLSEF[J].Control and Decision,1995,11(3):221-225.