在线建模的开关磁阻电机四象限运行无位置传感器控制

张旭隆 谭国俊 蒯松岩 刘送永 王其虎

（中国矿业大学信息与电气工程学院 徐州 221008）

1 引言

开关磁阻电机（Switched Reluctance Motor，SRM）的定、转子为双凸极结构，转子无绕组，具有结构简单、成本低、可靠性高等优点，已在牵引提升、航空工业、电动汽车等领域得到应用[1,2]。SRM需要转子位置传感器提供的位置信号来激励或关断相绕组，并由位置信号构成转速闭环，实现自同步运行[2]。然而位置传感器削弱了SRM 结构简单的优势、增大了系统的体积和成本，更降低了系统的可靠性，尤其是在潮湿、振动、多尘等应用场合。因此无位置传感器控制技术一直是SRM 领域的研究热点。

目前，国内外学者提出了多种可行的无传感器控制方案，如电流波形监视法[3]、磁链电流法[4,5]、电感模型法[6,7]、神经网络法[8-10]和状态观测器法[11-13]等。文献[11]中Luenberger观测器计算量大、对参数变化敏感，其在重载运行下的观测性能和鲁棒性有待提高。滑模观测器（Sliding Mode Observer，SMO）对SRM的非线性特性及参数变化具有良好的自适应性，可进行连续的位置估计，为SRM无传感器控制提供了新的思路。文献[12]首次提出SMO用于SRM的转子位置估计，其采用线性电机模型而忽略了非线性特征。文献[13]对SMO进行改进，采用复杂的非线性函数对SRM特性拟合，计算量较大，需要高性能的浮点运算芯片。同时，SRM的建模是观测器设计中的关键问题，准确的电机模型可以提高观测性能和鲁棒性。文献[14]采用BP神经网络对SRM进行建模，文献[15]采用径向基函数(Radial Basis Function，RBF)神经网络对SRM进行建模，这些方法均需通过离线测试获取SRM特性数据。文献[16]采用脉冲注入法在低速范围实现了SRM无传感器控制，但不可避免产生负转矩而影响电机输出转矩。文献[17]基于电感模型实现了全速度范围的SRM无传感器控制，但文中未涉及SRM的在线建模。

本文利用RBF 神经网络建立了相电流、磁链和转子位置角的非线性映射，以实际转子位置角与估计转子位置角相比较作为神经网络调节依据，给出了训练步骤。SRM 在线建模完成后，提出了激励脉冲法与滑模观测器相结合的四象限无传感器控制策略，利用数字信号处理器 DSP 与可编程控制器FPGA 芯片设计实现了无传感器SRM 控制器，并在18.5kW 样机上进行了实验。实验结果证实了该策略的有效性，对实现更大功率SRM 无传感器控制具有实际意义。

2 SRM的在线建模

2.1 RBF 神经网络结构

RBF 神经网络是具有单隐层的两层前向网络，其输入层到隐含层的变换是非线性的，而隐含层到输出层的变换是线性的[14,15]。SRM的磁链、相电流与转子位置角度三者之间存在唯一的映射关系[1,2]，以相电流和磁链为输入变量，转子位置角为输出变量，ai(x)为第i个隐含层神经元。RBF 神经网络的拓扑结构如图1 所示。输入变量为

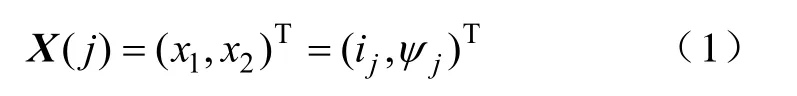
隐含层径向基函数采用高斯激活函数

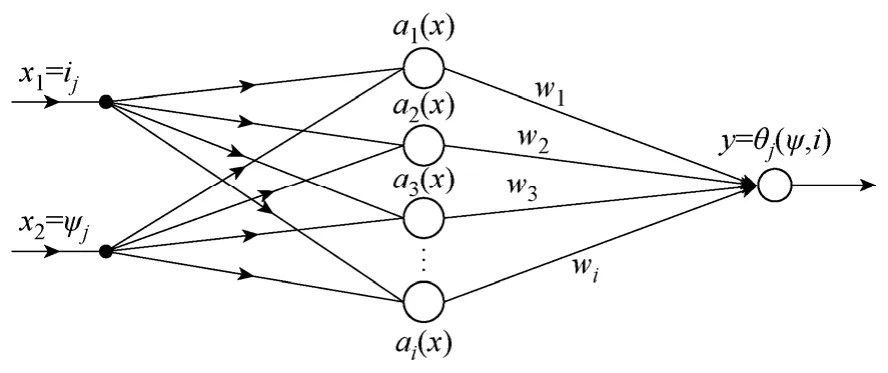
图1 RBF 神经网络的结构Fig.1 Structure of RBF neural network

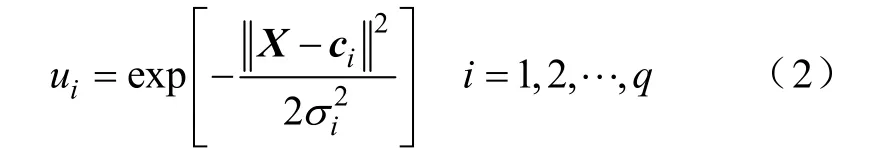
式中ui—隐含层第i个隐节点的输出；

σi—第i个隐节点的标准化常数；

q—隐含层节点数；

ci—第i个隐节点高斯函数的中心矢量，是与输入样本X维数相同的列矢量。

转子位置角度作为RBF 神经网络的输出

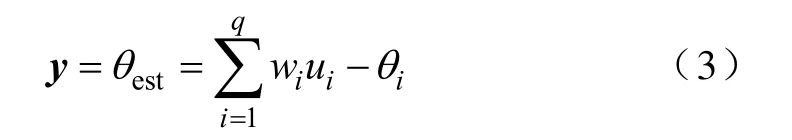
式中wi—隐含层到输出层的加权系数；

θi—隐含层的阈值。

2.2 RBF 神经网络的学习过程

在神经网络学习过程中，通过轴编码器获取实时的转子位置角度，模数转换（ADC）芯片实时采样电压和电流，同时DSP 根据SRM的绕组电压方程计算磁链。以磁链和相电流为输入，RBF 神经网络输出的估算转子位置角度θest与实际转子位置角度θact相比较，作为神经网络的调节依据。RBF 神经网络的在线学习过程如图2 所示。

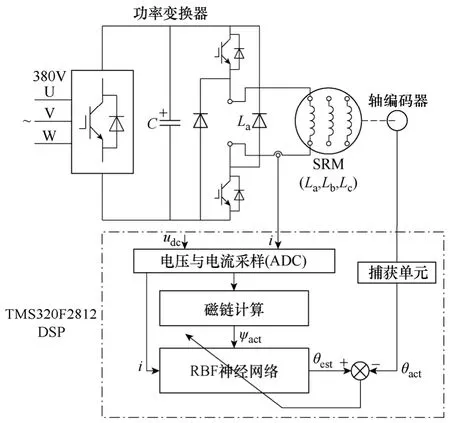
图2 RBF 神经网络的在线学习过程Fig.2 Online learning process of RBF neural network

RBF 网络的学习过程分为两个阶段：第一阶段，根据所有的输入样本决定隐含层各节点的高斯激活函数的中心矢量ci和标准化常数σi；第二阶段，在决定好隐含层的参数后，根据样本，利用递推最小二乘法，求出隐含层和输出层间的权值wi，并且可在完成第二阶段的学习后，再根据学习样本数据，同时校正隐含层和输出层的参数，以进一步提高网络精度。对于第j个学习样本（X(j)，yj），其具体学习步骤如下：

（1）分别按式（2）和式（3）计算RBF 神经网络各隐含层单元的输出ui(Xj)和网络的输出yj。

（2）计算轴编码器获得的转子位置角与RBF 神经网络输出之间的误差及样本与 已存在的隐含层单元的距离

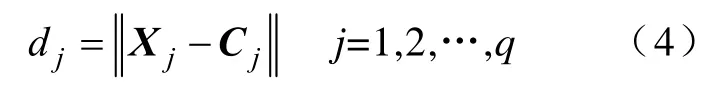
式中q—已存在的隐含层神经元个数。

（3）令dmin=min(dj)，若满足条件

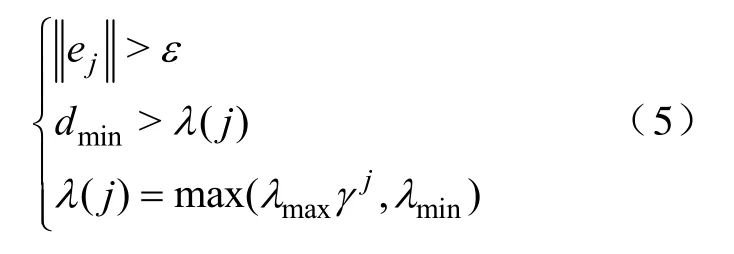
式中ε—网络期望精度；

λ(j)—第j个输入时网络的拟合精度，随着学 习的进行，λ(j)从λmax减小到λmin；

γ—衰减因子，0＜γ＜1。

即期望输出与实际输出间的误差大于设定精度，则增加一个隐含层神经元。

（4）否则，按递推最小二乘法调节网络连接权值。

（5）若对于连续输入的N个样本都满足式（6），则将第i个隐层单元删除。

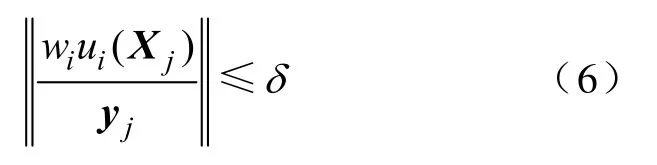
式中δ—预定义的常数（取N=100）。

（6）输入第j+1 个样本，重复上述过程。

3 静止状态下的初始转子位置估计

由SRM 基本电路方程可知

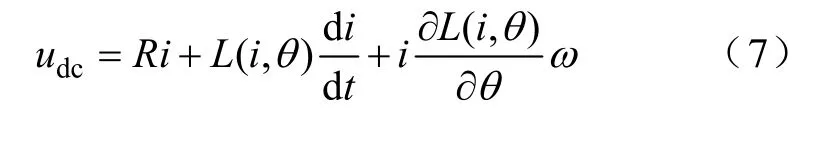
式中udc—直流电压；

L(i，θ)—相电感；

静止状态下的激励脉冲法原理如图3 所示。

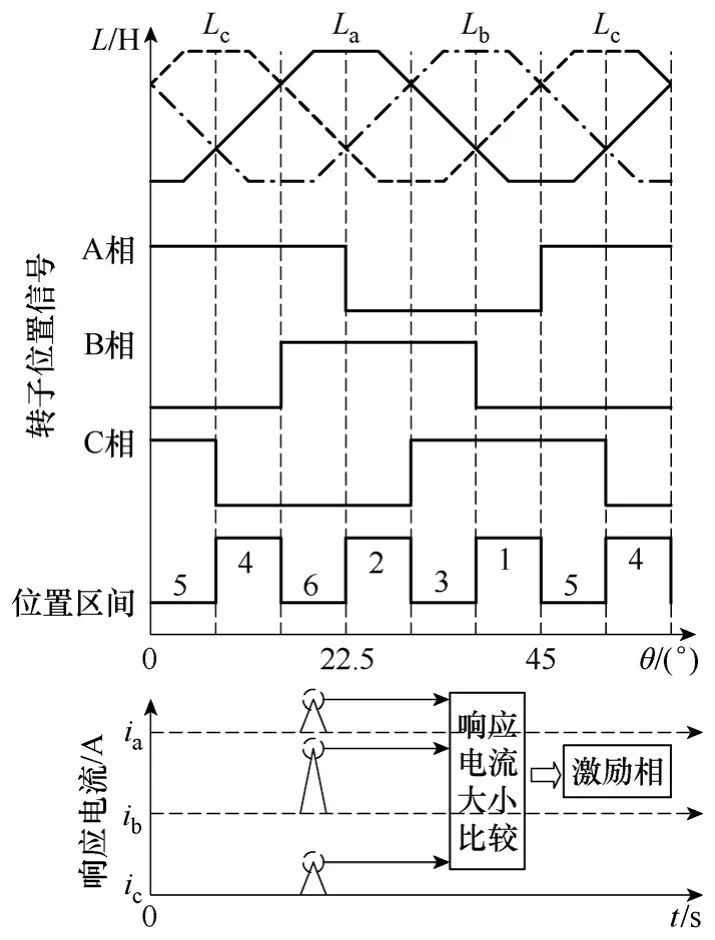
图3 激励脉冲法原理Fig.3 Principle of excitation pulse method

在电机静止起动瞬间，对SRM 通以短时的电压脉冲激励。由 于i∂L(i,θ)/(∂θ)ω=0，因此在忽 略绕组电阻压降的情况下，式（7）简化为

依次对电机三相绕组通以64μs的激励脉冲，得到相应的响应电流，比较响应电流的大小从而决定起动时的导通相。为保证位能负载下无反转启动及避免启动过程中出现转矩输出不足的情况，激励相的选择见下表。

表 SRM 电动运行激励相选择Tab. Excitation phase selection under motoring operation

4 滑模观测器转子位置估计

4.1 滑模观测器的设计

基于SMO的间接位置估计原理图如图4 所示，其以电机相电流与估计电流之间的误差作为输入量，输出量为转子位置角度和速度的估计值。

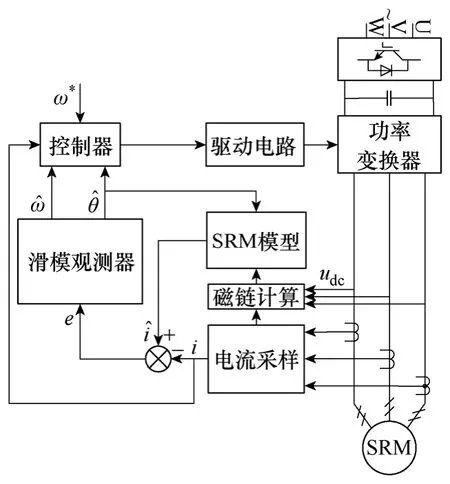
图4 滑模观测器无位置传感器控制结构Fig.4 Structure of sensorless control based on SMO

三相SRM的全阶滑模观测器可由下式描述[12-13]

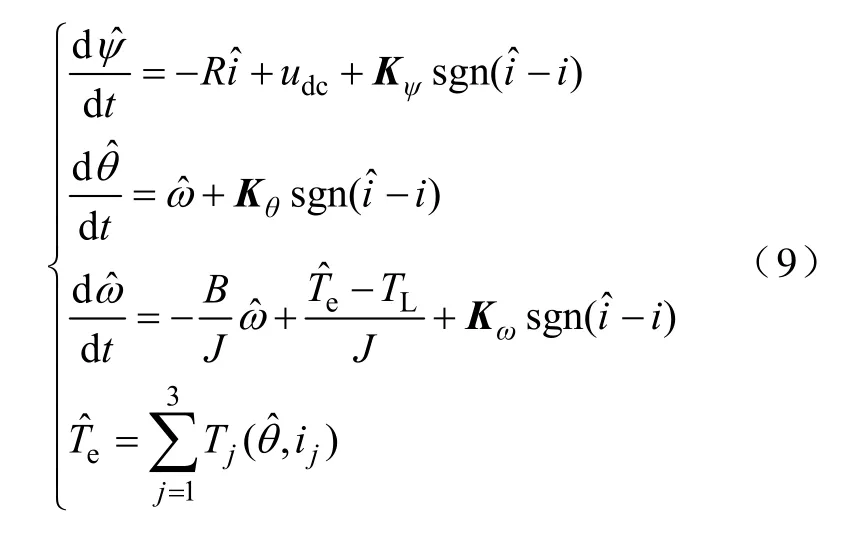
B—摩擦系数；

J—转动惯量；

KΨ—对角矩阵，Kψ=diag（kψ kψ kψ kψ）；

Kθ，Kω—行矢量，保证滑模状态的反馈系数，且Kθ=kθ（1111），Kω=kω（1111）；

相电流与磁链在每个电周期内都恢复为初值0，因而减小了积分误差的积累。同时通过准确的磁链观测计算，磁链估计值与真实值的误差极小，即，可忽略不计。由于瞬态负载转矩TL难以准确测量或估计，可将其作为系统的扰动项处理。在此前提下，电磁转矩的估计值不予保留，同样摩擦力项B/J相对很小也作为扰动项处理，对式（9）进行降阶，可得如下二阶滑模观测器

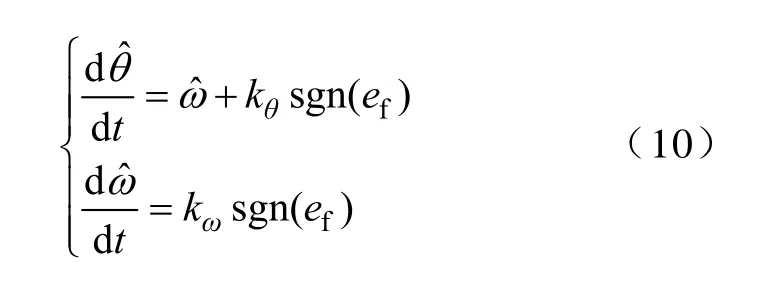
式中，ef为实际相电流与估计相电流之间的误差函数，间接地反映了实际转子位置与估计转子位置的误差，ef由下式定义

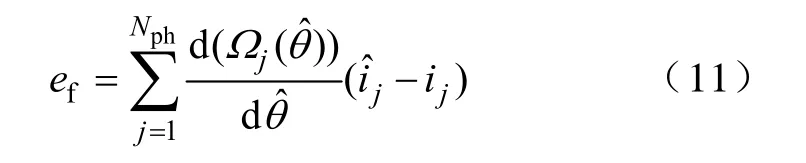
Nph—电机相数；

Nr—转子极数。

Ωj(θ)的作用是确保滑模观测器微分方程的收敛性，且保证了ef的符号不受电机运行模式变化的影响。

定义观测器的估计误差为

式（12）对t求导，将式（10）代入可得

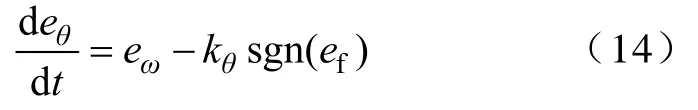
同理，式（13）求导后代入式（10），并结合式（9）可得

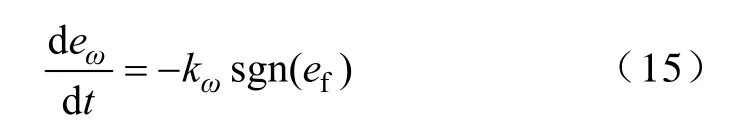
因此SMO 由间接反映转子位置误差的ef主导进入滑动面，即估计相电流与实际相电流之间的误差函数ef=0 意味着转子位置误差eθ=0。由式（14）、式（15）可知，通过合理的选择系数kθ和kω，可使eθ=0，系统状态进入误差为零的滑动平面。

为进一步分析滑模观测器的收敛性，定义李雅普诺夫函数（Lyapunov）为

对式（16）求导可得

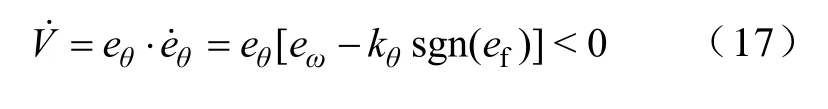
式（17）为滑模观测器的滑模面存在及可达的条件，为保证滑模观测器的快速收敛性，引入一个正常数η，增强式（17）的条件为

求解式（18）得到滑模状态的条件为

4.2 四象限运行控制

静止状态下的激励脉冲法用于判断SRM的转子初始位置，在SRM 启动完成后，滑模观测器对SRM的转子位置角度进行估计，包括静止状态的全速度范围无位置传感器控制策略（见图5）。

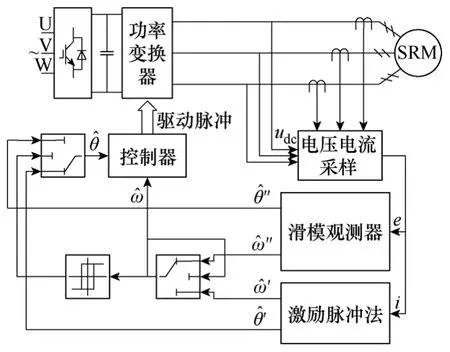
图5 全速度范围无传感器控制策略Fig.5 Sensorless control strategy over entire speed range

SRM 四象限运行原理如图6 所示，其中第I 象限为正向电动运行状态，第III 象限为反向电动运行状态，第II 象限为正向制动运行状态，第IV 象限为反向制动运行状态。SRM 在不同象限中运行的区别在于激励定子相绕组的切换顺序不同，同时配合不同的开通角、关断角即可实现。本文在额定转速以下采用固定角度的电流斩波控制（CCC）方式（其中电动运行时开通角为2°，关断角为18°；制动运行时开通角为24°，关断角为42°），而在额定转速以上采用角度位置控制（APC）方式。

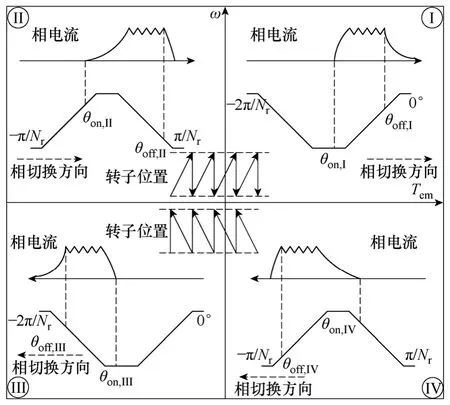
图6 开关磁阻电机四象限运行原理Fig.6 Principle of SRM four-quadrant sensorless control

5 实验验证

为验证本文所提控制策略的有效性，以DSP+FPGA 为控制系统核心，构建了实验平台（见图7），并以一台18.5kW SRM 为实验样机，进行了实验验证。以德州仪器（TI）公司的TMS320F2812 DSP 为核心控制芯片，负责静止启动转子初始位置判断、电机模型在线建模和SMO 转子位置估计、速度PI 调节及电流控制等功能。12 位的ADC 采样芯片ADS7864 负责实时采样，外扩512K的RAM存储器IS61LV51216 用于存放神经网络训练的实时数据，IGBT 开通关断信号经过 ALTERA 公司的EP1K30QC208 FPGA 逻辑综合处理后再送给驱动模块。功率变换器采用三相不对称半桥电路，主开关器件IGBT 采用英飞凌公司的FF150R12KE3G。样机额定参数：三相12/8 极，额定功率18.5kW，电源电压AC 380V，额定转速1 000r/min，最高转速1 350r/min。

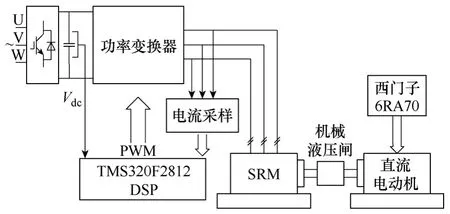
图7 SRM 实验平台结构Fig.7 Structure of SRM experimental bench

图8 为SRM 在第I 象限正向电动状态下的磁链、相电流及IGBT 门极脉冲波形，由图可知，电流波形为理想平顶波，其中的磁链由DSP 实时计算得到，并由D-A 芯片（DAC7724）输出。

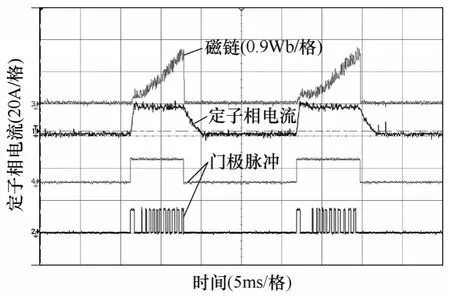
图8 磁链计算、相电流及IGBT 门极脉冲Fig.8 Flux linkage calculation,phase current and 1GBT gate pulse

图9 为SRM 在第I 象限电动状态下的转子位置估计、磁链及相电流波形，由图可知，最大位置估计误差≤2°，控制精度满足实际运行要求。

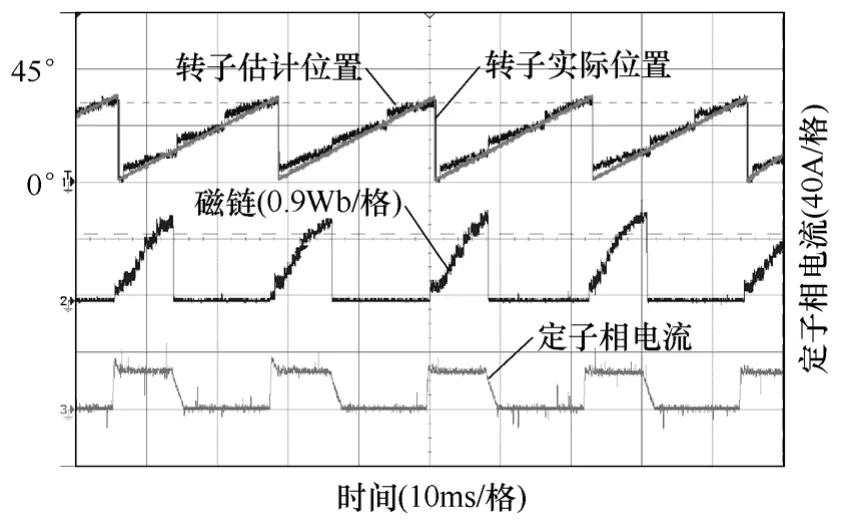
图9 电动状态下的转子位置估计Fig.9 Rotor position estimation of motor operation

图10 为SRM 由第I 象限到第III 象限转速反转过程中的转子位置估计波形。由图10 可知，转子实际角度与估计角度基本吻合，误差较小，象限间运行可靠。图11 为SRM 加速起动到额定转速，然后制动减速的过程。

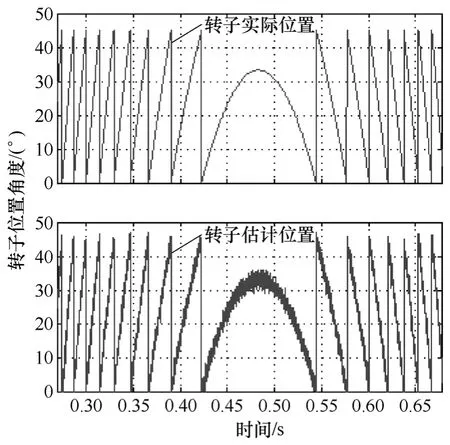
图10 速度反转过程中的转子位置估计Fig.10 Rotor position estimation when speed reversal

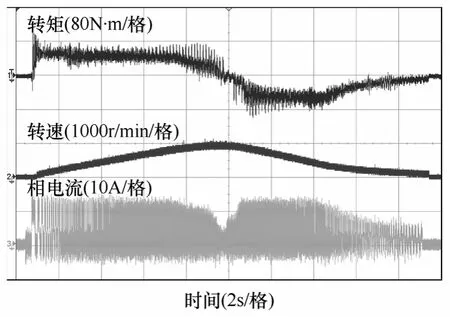
图11 系统加减速全过程Fig.11 Acceleration and deceleration period of SRM

SRM 样机的调速范围为100～1 350r/min，在满足静差度10%情况下，图12 为最低速时的机械特性，低速时的转矩脉动范围为150～230N·m。

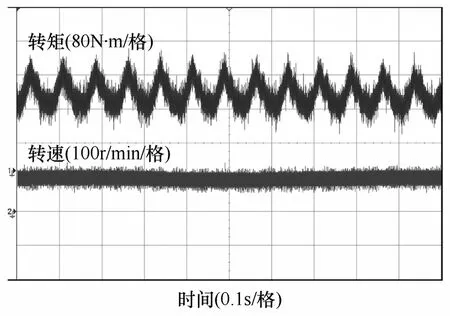
图12 转速为100r/min 时机械特性Fig.12 Mechanical characteristics when speed is 100r/min

对系统给定某一转速，待转速稳定后，逐渐增大负载，同时观察电流波形与转速值；当相绕组电流达到最大电流值，若继续增加负载，SRM 转速明显降低（大于允许动态速降）时，记录转速与容许输出转矩值。经多次测量，得到SRM 样机的机械特性如图13 所示，由图可知，SRM 在额定转速以下呈现恒转矩特性，额定转速至最高转速之间为恒功率特性。

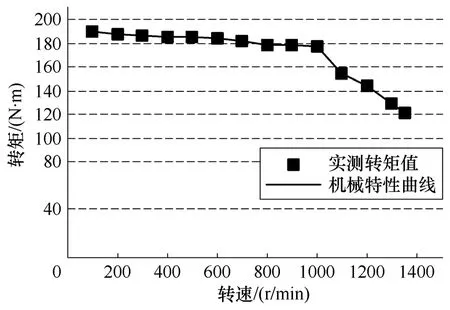
图13 SRM 样机实测机械特性Fig.13 Mechanical characteristics of SRM

图14a 为低速100r/min 时突加突减额定负载的动态速降，在3s 时突加负载，并在7.2s 时突减负载，测出动态速降为 25r/min。图 14b 为高速1 000r/min 时突加突减额定负载的动态速降，在1.8s时突加负载，并在4.2s 时突减负载，测得动态速降为70r/min。由图14 可以看出，在突加突减负载情况下，转矩、电流响应迅速，系统总能稳定至给定转速，说明抗干扰能力较好。

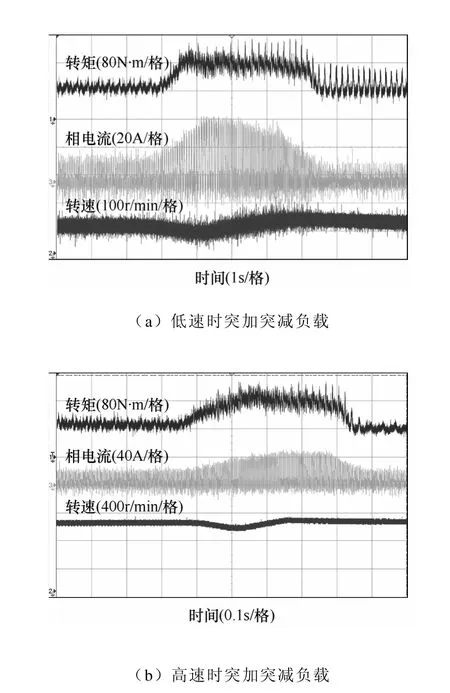
图14 突加突减负载时系统抗干扰能力实验波形Fig.14 Anti-interference ability of abrupt change load

6 结论

（1）本文建立了以相电流和磁链为输入、转子位置角度为输出的RBF 神经网络，实现了SRM的在线建模，避免了离线堵转实验或有限元分析获取SRM 特性数据，对大功率SRM 磁链特性建模有实际意义。

（2）在SRM 在线建模完成的基础上，提出了激励脉冲法与滑模观测器相结合的无位置传感器SRM 四象限运行控制策略。

（3）设计实现了以DSP+FPGA 为核心的SRM无位置传感器控制器，通过SRM 与直流机的对拖实验，验证了系统具有良好的动静态性能，转子位置估计误差较小，满足SRM 无位置传感器运行要求。本文所提出的控制策略有效可行，对进一步实现更大功率的开关磁阻电机无位置传感器控制具有借鉴意义。

[1]Krishnan R.Switched reluctance motor drives:modeling,simulation,analysis,design and applica-tions[M].Boca Raton,FL:CRC Press,2001.

[2]王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,1995.

[3]Acarnley P P,Hill R J,Hooper C W.Detection of rotor position in stepping and switched reluctance motors by monitoring of current waveforms[J].IEEE Transactions on Industrial Electronics,1985,32(3):215-222.

[4]Gallegos L G,Kjaer P C,Miller T J E.High-grade position estimation for SRM drives using flux linkage /current correction model[J].IEEE Transactions on Industry Applications,1998,34(4):859-869.

[5]邱亦慧,詹琼华,马志源,等.基于简化磁链法的开关磁阻电机间接位置检测[J].中国电机工程学报,2001,21(10):59-62.Qiu Yihui,Zhan Qionghua,Ma Zhiyuan,et a1.The indirect position sensing of SRM on the basis of simplified flux method[J].Proceedings of the CSEE,2001,21(10):59-62.

[6]Gao Hongwei,Salmasi F R,Ehsani M.Inductance model-based sensorless control of the switched reluctance motor drive at low speed[J].IEEE Transactions on Power Electronics,2004,19(6):1568-1573.

[7]陈坤华,孙玉坤,吴建兵,等.基于电感模型的开关磁阻电机无位置传感技术[J].电工技术学报,2006,21(11):71-75.Chen Kunhua,Sun Yukun,Wu Jianbing,et al.Inductance model-based sensorless control of the switched reluctance motors[J].Transactions of China Electrotechnical Society,2006,21(11):71-75.

[8]Lin Zhengyu,Reay D S,Williams B W,et al.Online modeling for switched reluctance motors using B-Spline neural networks[J].IEEE Transactions on Industrial Electronics,2007,54(6):3317-3322.

[9]夏长亮,王明超,史婷娜,等.基于神经网络的开关磁阻电机无位置传感器控制[J].中国电机工程学报,2005,25(13):123-128.Xia Changliang,Wang Mingchao,Shi Tingna,et al.Position sensorless control for switched reluctance motors using neural network[J].Proceedings of the CSEE,2005,25(13):123-128.

[10]夏长亮,谢细明,史婷娜,等.开关磁阻电机小波神经网络无位置传感器控制[J].电工技术学报,2008,23(7):33-38.Xia Changliang,Xie Ximing,Shi Tingna,et al.Position sensorless control of switched reluctance motor using wavelet neural networks[J].Transactions of China Electrotechnical Society,2008,23(7):33-38.

[11]Elmas C,Parra H Z L.Application of a full-order extended Luenberger observer for a position sensorless operation of a switched reluctance motor drive[C].IEE Proceedings of Control Theory and Applications,1996:401-408.

[12]Husain I,Sodhi S,Ehsani M.A sliding mode observer based controller for switched reluctance motor drives[C].Proceedings of IEEE Industry Applications Society Conference,1994:635-643.

[13]Islam M S,Husain I,Veillette R J,et al.Design and performance analysis of sliding-mode observers for sensorless operation of switched reluctance motors[J].IEEE Transactions on Control Systems Technology,2003,11(3):383-389.

[14]蔡燕,许镇琳,高超.基于神经网络非线性模型的开关磁阻电机调速系统动态仿真[J].电工技术学报,2006,21(8):25-30.Cai Yan,Xu Zhenlin,Gao Chao.Simulation of SRD based on neural net nonlinear model[J].Transactions of China Electrotechnical Society,2006,21(8):25-30.

[15]纪良文,蒋静坪,何峰.基于径向基函数神经网络的开关磁阻电机建模[J].电工技术学报,2001,16(4):7-11.Ji Liangwen,Jiang Jingping,He Feng.Modeling of switched reluctance motors based on radial basis function neural network[J].Transactions of China Electrotechnical Society,2001,16(4):7-11.

[16]Komatsuzaki A,Bamba T,Miki I.A position sensorless speed control for switched reluctance motor at low speeds[C].IEEE Power Engineering Society General Meeting,2007:1-7.

[17]Fahimi B,Emadi A,Sepe R B.Four-quadrant position sensorless control in SRM drives over the entire speed range[J].IEEE Transactions on Power Electronics,2005,20(1):154-163.