基于滑模观测器的单绕组多相无轴承电机无位置传感器控制
程 帅 姜海博,2 黄 进 康 敏
(1.浙江大学电气工程学院 杭州 310027 2.中国电力工程顾问集团 北京 100000 3.浙江科技学院电气学院 杭州 310023)
1 引言
无轴承电机是近年来发展起来的一种新型悬浮电机,通过气隙中极对数差为1的两组磁场相互作用,产生电磁转矩和径向悬浮力,同时实现电机的自旋转和自悬浮。无轴承电机省去了传统轴承的机械支撑,使其在高速机床、飞轮储能等领域有着广泛的应用前景;此外无轴承电机在加工洁净要求很高或转子不存在摩擦的场合,如半导体工业、人工心脏等场合也有很高的应用价值[1-5]。
传统的无轴承电机采用两套极对数相差为1的绕组,一套提供转矩,另一套提供悬浮力。目前对无轴承电机的研究主要集中在数学模型、本体设计、先进控制算法及控制系统上[1-11]。单绕组无轴承电机主要有桥式[2]、裂相[3]和多相结构[4,5]。文献[9]中提出了一种单绕组无轴承永磁薄片电机,其定子结构与裂相式电机的结构类似,采用注入两组相位差不同电流的方式实现电机的平稳悬浮,其控制效果优于裂相式加正负电流的控制方式。文献[10]还对二相无轴承薄片电机的驱动及其控制方法进行了研究,提出了一种交错并联的半桥拓扑结构,有效地减少了功率管的数量。多相单绕组无轴承电机采用定子不对称结构,每相绕组函数中存在基波和2 次空间谐波,通过在电机绕组中注入两组相位差不同的电流可以在一台多相电机的两个平面内产生两个极对数相差为1的磁场,进而产生悬浮力,维持电机稳定悬浮。文献[11]以一台五相单绕组电机为例,对其空间矢量脉宽调制(SVPWM)进行了研究,控制谐波平面空间电压矢量实现了电机平稳悬浮。
无轴承电机转子的速度信号的精确获取是其稳定运行的保证。但是机械式传感器的存在增加了系统的复杂程度,给系统带来了安装、连线和可靠性的问题,尤其是在恶劣环境下运行时提取信号的准确性无法得到保证。在高速运行场合,普通的速度传感器如光电编码盘的应用也会受到限制。将无位置传感器技术应用到无轴承领域既可以克服传统测速装置存在的问题,也可以降低成本,对无轴承技术的工业化有着重要的意义。
基于滑模观测器的永磁同步电机无位置传感器控制是该领域研究的一个热点。该算法控制算法简单,对系统数学模型精确度要求不高,对系统参数变化、外界扰动具有自适应性,有很强的鲁棒性[12-18]。
本文针对多相单绕组无轴承电机的数学模型,考虑悬浮平面与转矩平面的耦合,采用滑模观测器辨识电机的旋转反电动势实现了该电机的无位置传感器运行,实验结果证明了所述方法的有效性和可行性。
2 针对单绕组多相无轴承电机的滑模观测器原理
2.1 单绕组多相永磁型无轴承电机的数学模型
五相单绕组永磁型无轴承电机利用五相电机中存在的两个控制自由度同时实现电机的自旋转和自悬浮[4]。可以通过式(1)的坐标变换矩阵将电机中相平面的各物理量转换到五相电机的两个相互正交的dq 平面内。式中前两行对应于电机的转矩平面,为电机提供电磁转矩维持电机的平稳旋转,第3、4行对应于电机的悬浮平面,为电机提供悬浮力,进而使电机在没有机械轴承支撑的情况下始终围绕电机中心旋转。

式中φ——电机转角;
γ=2π/5。
对于一个无轴承驱动系统,其转矩平面和悬浮平面存在关于转子偏心的耦合。考虑转子的偏心,转子定向后,五相单绕组永磁型无轴承电机的电压方程可以表示为[4]


式中L1m,L2m——d1-q1 平面和d2-q2 平面的等 效电感;
M——两平面之间互感与电机转子位移的比值,为一固定常数;
x,y——电机转子在水平和垂直方向上的位移偏心;
ω——电机转速;
If——等效励磁电流;
fd1s,fq1s,fd2s,fq2s——电机的各物理量在转矩平面和悬浮平面d 轴和q 轴的分量;
f——电机的电压、电流、磁链等。
无轴承电机通过控制电机两组极对数不同的磁场,相互作用,产生可控悬浮力,悬浮力的数学表达式为[4]

式中g0——气隙长度;
ψf——转子等效磁链;
Fα,Fβ——径向悬浮力分量。
通过控制转矩平面和悬浮平面的电流,为电机提供电磁转矩,并克服电机重力和单边磁拉力,维持电机在转子中心平稳旋转。
2.2 无轴承电机的滑模观测器原理
将电压方程转化到静止坐标系下,由式(2)得

式中

p——微分算子;
fα1,fβ1,fα2,fβ2——静止坐标系中转矩平面和悬浮平面中α,β 轴电压、电流分量;
eα1,eβ1——静止坐标系中转矩绕组的反电
动势在α,β 轴上的分量;
θ——电机位置角;
Rs——定子电阻;
ω——转子角速度。
由式(5)可以发现,转矩绕组的反电动势中包含转子的位置信息θ,通过估算转矩绕组中反电动势的变化就可以提取出转子的机械位置角度,进而获得转速信息。若令
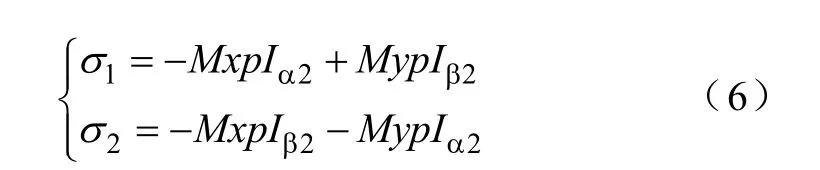
将式(6)代入式(4)可得

由式(7)可知,区别于传统的永磁同步电机数学模型,由于转子偏心的影响,无轴承电机中存在一定的耦合,而耦合项σ1、σ2的大小与转子偏心、悬浮电流以及电机转速有关,与电机转角不存在直接的关系,会对电机的位置辨识造成一定的周期性影响。
图1 为滑模观测器的设计框图,若令ˆf表示该 物理量的观测值,根据五相单绕组永磁型无轴承电机在静止坐标系下的数学模型和滑模变结构理论,可以定义滑模面为
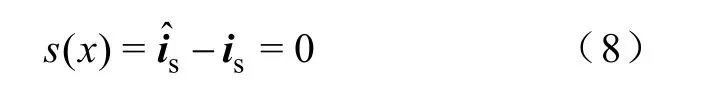
构造滑模观测器为[12]

式中,kslide为滑模增益,滑模存在条件可由 Lyapunov 第二方法得到,即若取Lyapunov 函数为:,则滑模运动在全局范围内渐进稳定的条件为

图1 滑模观测器结构图Fig.1 The structure of sliding mode observer
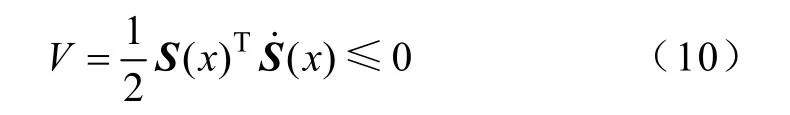

由式(11)可知,当kslide满足,时满足滑模观测器的稳定条件,可以产生滑动模态运动。经过有限的时间后,系统进入滑动模态并达到稳定,此时有,且代入式(9)与式(7)的作差获得的估算电流误差动态模型,有

如式(12)所示,由z表示的切换信号包含了系统的反电动势信息,电机偏心引入的扰动以及其他各种形式的外部扰动,由于无轴承电机悬浮运行时,电机转子偏心很小,所以切换信号中反电动势信息占主导地位。区别于传统的基波反电动势辨识方法,对于无轴承系统,此方法中由电机偏心引起的无轴承电机固有扰动可以被观测器方程中的滑模切换信号所湮没,此外还对参数不确定性及外部扰动具有很强的鲁棒性和自适应性。
为了改善辨识的反电动势波形,提高转子位置角辨识的准确性,实验中采用饱和函数替代传统的开关切换函数,饱和函数可以写为[12]

式中,ξ为边界层,其取值过大导致系统响应时间过长,过小导致饱和函数效果不明显,参数辨识精度下降。
由式(13)饱和函数输出通过低通滤波器可以提取出反电动势的信息,进而获得转子的位置信息。低通滤波器的截止频率过大,滤波效果不明显,会导致反电动势的失真;截止频率过小,会导致系统的延迟比较明显,所以引入了变频率滤波和转角补偿环节,滤波器的截止频率选取与电机的实际转速有关。滤波器的表达式可以写为[12]

从式(14)可以看出,该低通滤波器的截止频率为ω/τ,τ为常数,不同转速下该滤波器截止频率随之变化。
相移补偿可以表示为

电机的转角估计值为

值得注意的是,选取较大的滑模切换增益有利于提高系统的稳定性,但是太大的滑模增益会使得定子电流的估算值和反电动势估算值产生畸变,因此可以根据电机的转速实时调整切换增益值:kslide=k0ω,k0为常数,使得电机在低速和高速范围内均可以取得比较理想的效果。
3 控制策略
基于滑模观测器的无位置传感器控制框图如下图2 所示,系统主要由三个部分组成,即转矩绕组控制器、悬浮绕组控制器及电机本体组成。
滑模观测器通过检测转矩绕组的电流以及给定电压的参考值来获得转子的位置信号以及转速信号。速度估算信号与速度参考值比较后的误差经过PI 调节器产生相应的转矩绕组q 轴电流参考值,与系统反馈的电流实际值相比较后的误差经过PI 调节器产生相应的转矩绕组q 轴电压参考值;从电涡流位移传感器获得的径向位移信号与参考位置比较后的误差经过PID 调节器分别得到径向的可控悬浮力,通过悬浮电流的数学模型获得悬浮绕组电流的参考值,同样经过PI 调节器得到悬浮平面的d、q轴电压参考值。
利用滑模观测器观测的电机位置转子信息,经过坐标变换后得到静止坐标系下的电压参考值,作为SVPWM 控制的输入信号,实现电机的无位置传感器稳定运行。
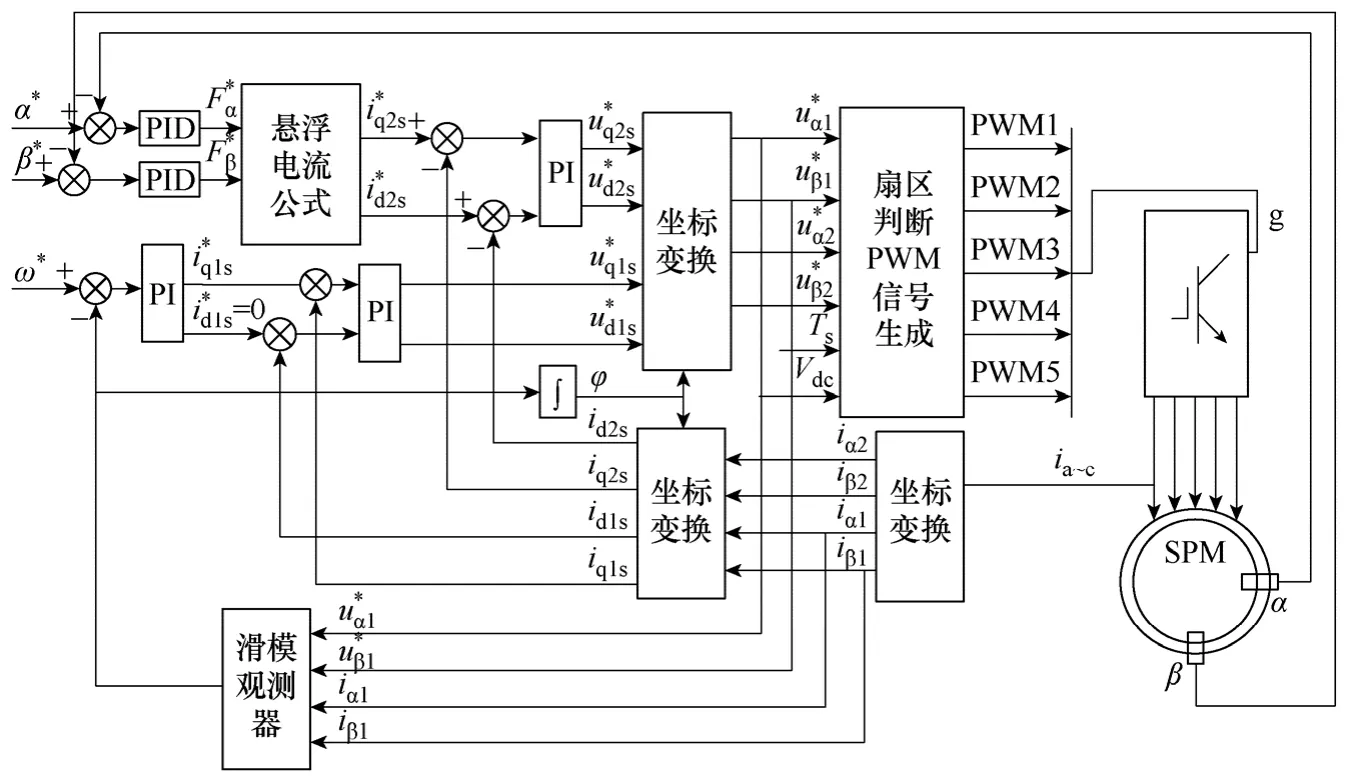
图2 无轴承电机无位置传感器控制框图Fig.2 The position sensorless control diagram of the bearingless motor
4 实验结果
实验样机为一台4kW的五相单绕组永磁型无轴承电机,设计时引入机械辅助轴承将轴限制在±0.33mm的范围内防止定转子直接接触。样机额定电压为140V,额定电流为6.3A。电机参数见下表。
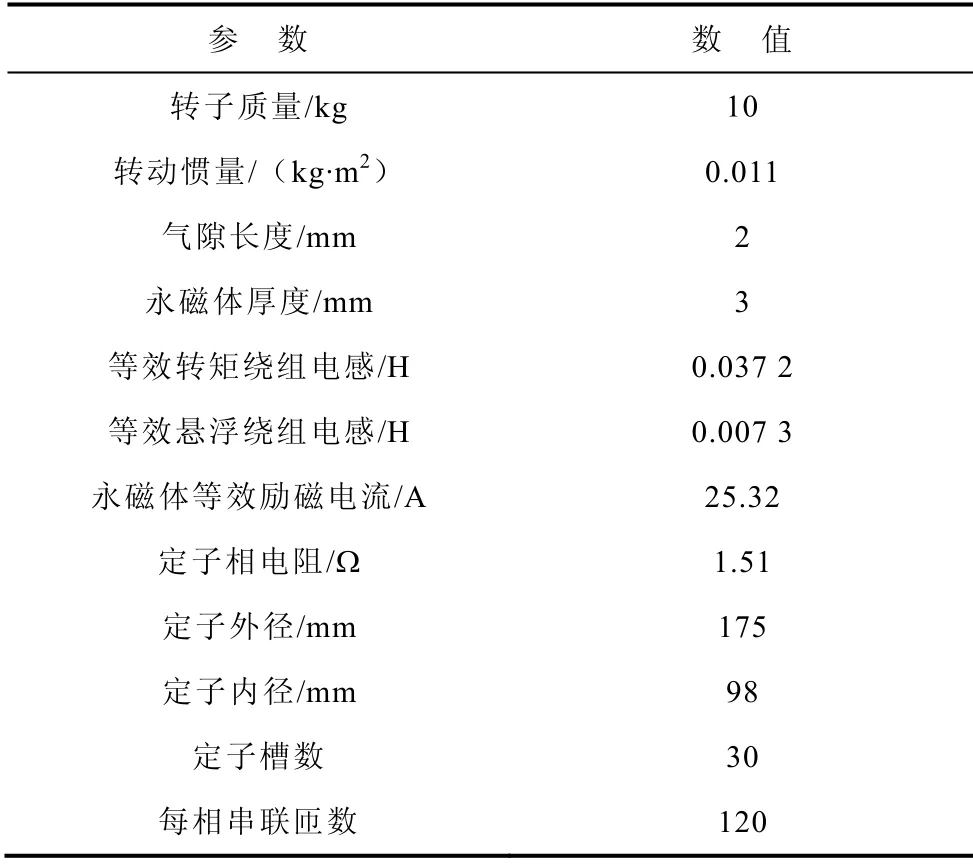
表 样机参数Tab Parameters of the prototype
图3 和图4 为电机采用滑模观测器在升速过程中(500~1 200r/min)的实验结果。图3 表示加速过程电机的α、β 方向上的估算反电动势,电机转角的实际值(光电编码盘测得)和估算值和电机的径向转子位移,由图可见电机在加速过程中一直可以平稳悬浮。图4 为图3 中电机在500r/min 时反电动势和转角的局部放大图,由图可见,电机估算反电动势正弦度良好,估算角度与实际角度基本吻合。
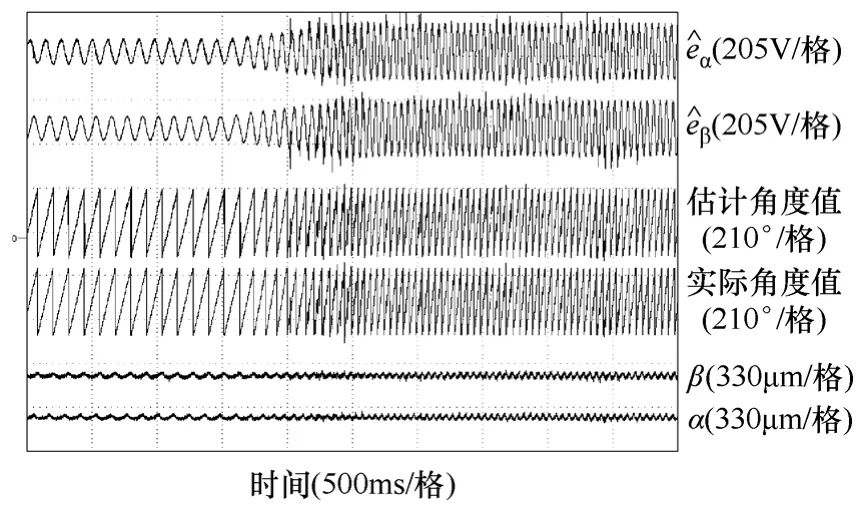
图3 观测反电动势、估算转角、实际转角、位移偏心 实验波形Fig.3 Estimated EMF,rotor positon and actual angle,rotor eccentricity waveforms

图4 500r/min 反电动势及电机转角误差波形Fig.4 Estimation error of speed and rotor positon
图 5 反映了电机在升速过程中(500~1 200 r/min)转矩平面静止坐标系下电流的实测值和估计值,如图所示,滑模观测器在电机稳态和动态悬浮时均可以很好实现对实际电流信号的观测。图6 为升速过程中无轴承电机实际转速、估计转速、转子电流和悬浮电流的波形。

图5 升速过程中α、β 轴电流实际值和估计值Fig.5 Estimated and actual current at speed up

图6 升速过程中转速的实际值、估计值,转子电流 和悬浮电流Fig.6 Estimated and actual speed,current of rotation and suspension plane at speed up
图7 为施加悬浮力扰动时滑模观测器辨识的实验结果。在分隔线左边,在外部施加了一定的悬浮力扰动;而在分隔线右边,扰动撤除。实验结果表明电机在施加悬浮力扰动时,该数学模型仍可以较为准确的辨识电机的转角信息,维持电机的旋转和平稳悬浮。图8 为施加悬浮力扰动及电机结构的示意图。

图7 存在悬浮力扰动时的转角辨识波形Fig.7 Estimation results at suspension disturbance
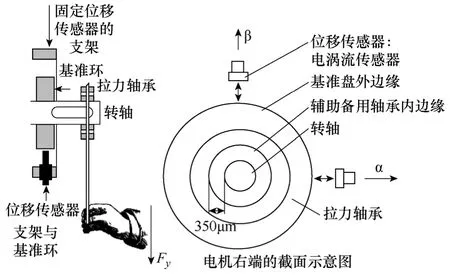
图8 施加悬浮力扰动及电机结构示意图Fig.8 Schematic diagram of suspension disturbance and motor structure
5 结论
本文根据单绕组多相无轴承电机的数学模型和滑模变结构理论,实现了基于滑模观测器的无位置传感器控制。区别于传统的永磁同步电机无传感器控制,分析了悬浮平面对转角辨识的影响,并给出了实验波形。实验结果表明,该控制算法能够实现转子的稳定悬浮和无速度传感器运行,且在存在悬浮力扰动时也具有良好的动、静态运行性能。
[1]Chiba A,Deido T,Fukao T,et al.An analysis of bearingless AC motors[J].IEEE Transactions on Energy Conversion,1994,9(1):61-68.
[2]Khoo W K S.Bridge configured winding for polyphase self-bearing machines[J].IEEE Transac-tions on Magnetics,2005,41(4):1289-1295.
[3]Ribeiro R L A,Castro F E F,Salazar A O,et al.A suitable current control strategy for split-phase bearingless three-phase induction machine[C].IEEE 36th Conference on Power Electronics Specialists,2005:701-706.
[4]Jiang Haibo,Huang Jin,Kang Min.Principle and realization of a 5-phase PM bearingless motor drive[C].6th International Power Electronics and Motion Control Conference,2009:1852-1857.
[5]Huang J,Kang M,Yang J Q.Analysis of a new 5-phase bearingless induction motor[J].Journal of Zhejiang University Science A,2007,8(3):1311-1319.
[6]Boesch P,Barletta N.High power bearingless slice motor(3-4kW)for bearingless canned pumps[C].The 9th International Symposium on Magnetic Bearings,2004:155-161.
[7]廖启新.无轴承永磁薄片电机的研究[D].南京:南京航空航天大学,2005.
[8]康敏.单绕组多相无轴承电机的研究[D].杭州:浙江大学,2009.
[9]朱俊,邓智泉,王晓琳,等.单绕组无轴承永磁薄片电机的原理和实现[J].中国电机工程学报,2008,28(33):68-74.Zhu Jun,Deng Zhiquan,Wang Xiaolin,et al.Principle and implementation of the single winding bearingless permanent magnetic slice motor[J].Procedings of the CSEE,2008,28(33):68-74.
[10]Bartholet M T,Nussbaumer T,Krahenbuhl D,et al.Modulation concepts for the control of a two-phase bearingless slice motor utilizing three-phase power modules[J].IEEE Transactions on Industry Application,2010,46(2):831-840.
[11]姜海博,黄进,康敏.单绕组五相永磁无轴承电机的SVPWM 控制[J].电工技术学报,2011,26(1):34-39.Jiang Haibo,Huang Jin,Kang Min.SVPWM control for a 5-phase PM bearingless motor with single set of windings[J].Transactions of China Electrotechnical Society,2011,26(1):34-39.
[12]Chu Jianbo,Hu Yuwen,Huang Wenxin.An improved sliding mode observer for position sensorless vector control drive of PMSM[C].International Power Electronics and Motion Control Conference,2009:1898-1902.
[13]Hongryel Kim,Jubum Son,Jangmyung Lee.A high speed sliding mode observer for the sensorless speed control of a PMSM[J].IEEE Transaction on Industrial Electronics,2011,58(9):1-10.
[14]Jafarifar M,Kianinezhad R,Seifossadat S G.Sliding mode sensorless control of symmetrical six-phase induction machines[C].International Conference on Electrical and Electronics Engineering,2009:169-173.
[15]尚喆,赵荣祥,窦汝振,基于自适应滑模观测器的永磁同步电机无位置传感器控制研究[J].中国电机工程学报,2007,27(3):23-27.Shang Zhe,Zhao Rongxiang,Dou Ruzhen.Research on sensorless control method of PMSM based on an adaptive sliding mode observer[J].Proceedings of CSEE,2007,27(3):23-27.
[16]Liu Jiaxi,Yang Guijie,Li Tiecai.A new approach to estimated rotor position for PMSM based on sliding mode observer[C].International Conference on Electrical Machines and Systems,2007:426-431.
[17]陈东,贺益康,年珩,等.基于滑模观测器的永磁无轴承电机控制[J].电机与控制应用,2008,35(10):9-13.Chen Dong,He Yikang,Nian Heng.Control of permanent magnet bearingless motor based on sensorless operation[J].Electric Machines & Control Application,2008,35(10):9-13.
[18]郭清风,杨贵杰,晏鹏飞.SMO 在无位置传感器PMSM 驱动控制系统的应用[J].电机与控制学报,2007,11(4):354-358.Guo Qingfeng,Yang Guijie,Yan Pengfei.Application of SMO for sensorless driven and controlling system of PMSM[J].Electric Machines and Control,2007,11(4):354-358.

